509. 斐波那契数

Posted 2021-09-17 可持续化发展

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。

 

1、暴力递归

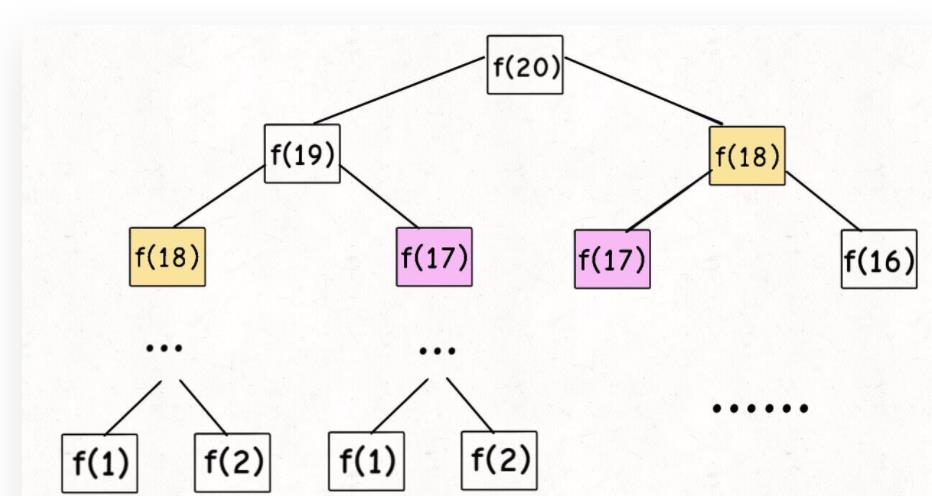
斐波那契数列的数学形式就是递归的，画一下递归树，暴力递归是从上往下递归到最低层（找到最底层，递归的终止条件），然后，从下往上依次递归出结果（把结果从最底层开始，通过不断的return，把结果计算出来）。

 

class Solution {
    public int fib(int n) {
    	if(n == 0) {
    		return 0;
    	}
    	if(n==1 || n==2) {
    		return 1;
    	}
    	return fib(n - 1)+fib(n - 2);
    }
}

2、带备忘录的递归解法

因为有重复计算，比如，f(18)计算了两次。

 

class Solution {
    public int fib(int n) {
    	// 备忘录全初始化为 0
        int[] memo = new int[n + 1];
        // 进行带备忘录的递归
        return helper(memo, n);
    }
    private int helper(int[] memo, int n) {
        // base case
        if (n == 0 || n == 1) return n;
        // 已经计算过，不用再计算了
        if (memo[n] != 0) return memo[n];
        memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
        return memo[n];
    }
}

3、dp 数组的迭代解法

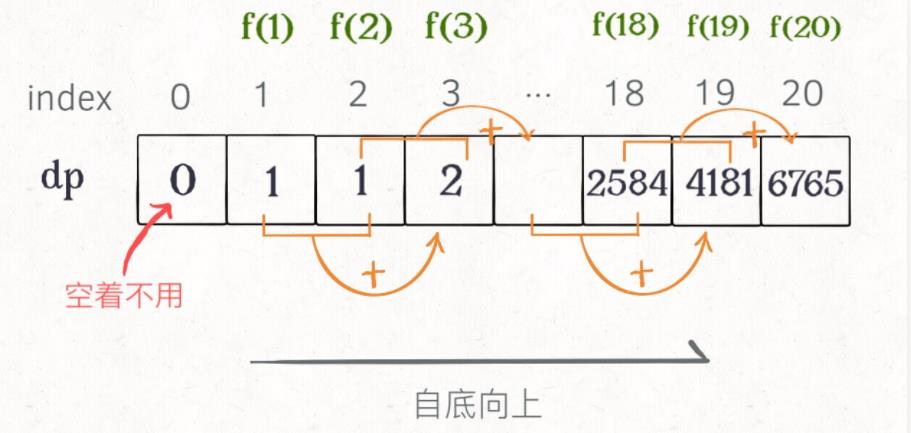
在一个数组中，完成「自底向上」的推算。

class Solution {
    public int fib(int n) {
    	if(n == 0) return 0;
    	int[] dp = new int[n + 1];
    	dp[0] = 0; dp[1] = 1;
    	//状态转移
    	for(int i = 2; i <= n; i++) {
    		dp[i] = dp[i-1] + dp[i - 2];
    	}
    	return dp[n];
    }    
}