字符串-后缀树和后缀数组详解
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了字符串-后缀树和后缀数组详解相关的知识,希望对你有一定的参考价值。

后缀树
建议先了解一下字典树。
首先理解后缀的概念,后缀(suffix)即从某个位置开始到末尾的一个子串。例如字符串 s = a a b a b s=aabab s=aabab,它的五个后缀为 a a b a b aabab aabab、 a b a b abab abab、 b a b bab bab、 a b ab ab、 b b b。
后缀树(suffix tree)就是把所有的后缀子串用字典树的方法建立的一棵树,如图:
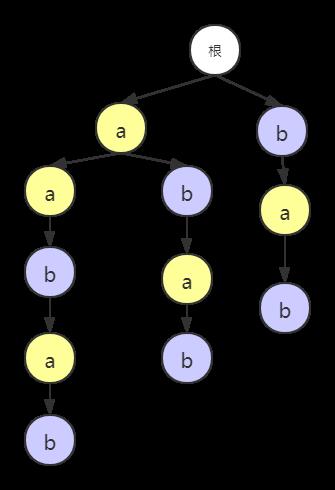
其中根节点为空,还可以在叶子节点后用一个’$'符标识结束,从根节点出发就能到达所有的子串情况。
模板:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100005;
int trie[maxn][26];
int pos = 1, n;
char s[maxn], t[maxn];
void insert(int idx) { //构建后缀树
int p = 0;
for (int i = idx; i < n; i++) {
int u = s[i] - 'a';
if (trie[p][u] == 0)
trie[p][u] = pos++;
p = trie[p][u];
}
}
bool find() { //查询是否是子串
int p = 0;
for (int i = 0; s[i]; i++) {
int u = s[i] - 'a';
if (trie[p][u] == 0)
return false;
p = trie[p][u];
}
return true;
}
int main() {
scanf("%s%s", s,t);
n = strlen(s);
for (int i = 0; i < n; i++) {//枚举起点
insert(i);
}
printf("%s子串", find() ? "是" : "不是");
return 0;
}
但是不难发现,建树的时间和空间成本都很高。后缀数组和后缀自动机可以看作是对后缀树时间和空间上的优化,通过映射关系避免建树和提高树节点重复利用率。
后缀数组
概念
直接对后缀树构造和编程不太方便,而后缀数组(suffix array)就是更简单的替代方法。
| 下标i | 后缀s[i] | 下标j | 字典序 | 后缀数组sa[j] |
|---|---|---|---|---|
| 0 | aabab | 0 | aabab | 0 |
| 1 | abab | 1 | ab | 3 |
| 2 | bab | 2 | abab | 1 |
| 3 | ab | 3 | b | 4 |
| 4 | b | 4 | bab | 2 |
后缀数组就是字典序对应的后缀下标,即 s a sa sa(suffix array缩写)数组。比如 s [ 1 ] = 3 s[1]=3 s[1]=3,表示字典序排1的子串,是原来字符串中第3个位置开始的后缀子串,即 a b ab ab。
通过后缀数组能方便的解决一些字符串问题,如在母串 s s s中查找子串 t t t,只需在 s a [ ] sa[] sa[]上做二分搜索,时间复杂度是 O ( m l o g n ) O(mlogn) O(mlogn),m子串长度n母串长度,如查找 b a ba ba:
#include<bits/stdc++.h>
using namespace std;
string s, t;
int sa[] = { 0,3,1,4,2 }; //设sa[]已求出
int find() { //t在s中位置
int l = 0, r = s.size();
while (r > l + 1) { //字典序里二分
int mid = (l + r) / 2;
if (s.compare(sa[mid], t.length(), t) < 0)
l = mid; //-1不相等移动左指针
else r = mid; //0相等移动右指针
}
if (s.compare(sa[r], t.length(), t) == 0)
return sa[r]; //返回原始位置
if (s.compare(sa[l], t.length(), t) == 0)
return sa[l];
return -1; //没找到
}
int main() {
s = "aabab";
t = "ba";
cout << find();
return 0;
}
sa[]
那现在的问题是如何高效的求后缀数组 s a [ ] sa[] sa[],即对后缀子串进行排序?
若直接使用快排,每两个字符串间还有 O ( n ) O(n) O(n)的比较,所以总的复杂度是 O ( n 2 l o g n ) O(n^2logn) O(n2logn),显然不够友好。答案是使用倍增法。
- 用数字替代字母,如a=0,b=1。
- 连续两个数字组合,如00代表aa,01代表ab,最后一个1没有后续,在尾部加上0,组成10,并不影响字符得比较。
- 连续4个数字组合,如0010代表aaba,同样得01和10没有后续,补0。
- 得到5个完全不一样的数字,可以区分大小了,进行排序,得到rk数组={0,2,4,1,3}。
- 最后通过排名得到后缀数组sa[]={0,3,1,4,2}。
| 步骤 | a | a | b | a | b |
|---|---|---|---|---|---|
| 第一步 | 0 | 0 | 1 | 0 | 1 |
| 第二步 | 00 | 01 | 10 | 01 | 10 |
| 第三步 | 0010 | 0101 | 1010 | 0100 | 1000 |
| 下标i | 0 | 1 | 2 | 3 | 4 |
| 排序rk[i] | 0 | 2 | 4 | 1 | 3 |
| 转换sa[i] | sa[0]=0 | sa[2]=1 | sa[4]=2 | sa[1]=3 | sa[3]=4 |
| sa[i] | 0 | 3 | 1 | 4 | 2 |
上述每一步递增两倍,总共 l o g ( n ) log(n) log(n)步,但是当字符串很长时,产生的组合数字就非常大可能溢出,这时就需要每一步都进行一个压缩,只要相对顺序不变即可,如下:
| 步骤 | a | a | b | a | b |
|---|---|---|---|---|---|
| 第一步 | 0 | 0 | 1 | 0 | 1 |
| 第二步 | 00 | 01 | 10 | 01 | 10 |
| 排序rk[] | 0 | 1 | 2 | 1 | 2 |
| 第三步 | 02 | 11 | 22 | 10 | 20 |
| 下标i | 0 | 1 | 2 | 3 | 4 |
| 排序rk[i] | 0 | 2 | 4 | 1 | 3 |
| 转换sa[i] | sa[0]=0 | sa[2]=1 | sa[4]=2 | sa[1]=3 | sa[3]=4 |
| sa[i] | 0 | 3 | 1 | 4 | 2 |
rk[]
也就是说求后缀数组 s a [ ] sa[] sa[],需要通过一个排名 r k [ ] rk[] rk[]来求。两者是一一对应的关系,互为逆运算,可以互相推导,即 s a [ r k [ i ] ] = i sa[rk[i]]=i sa[rk[i]]=i, r k [ s a [ i ] ] = i rk[sa[i]]=i rk[sa[i]]=i。
- sa[]后缀数组,suffix array缩写,记录的是位置,是字典序排名第i的是谁。
- rk[]排名数组,rank array缩写,记录的是排名,是第i个后缀子串排名第几。
那得到倍增后的相对大小数字后,我们可以直接用快排
s
o
r
t
(
)
sort()
sort()得到
r
k
[
]
rk[]
rk[],每次快排
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),需要快排
l
o
g
(
n
)
log(n)
log(n)次,总复杂度是
O
(
n
(
l
o
g
n
)
2
)
O(n(logn)^2)
O(n(logn)2)。
模板:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn], tmp[maxn + 1];
int n, k;
bool cmp_sa(int i, int j) { //直接比较,省去组合过程
if (rk[i] != rk[j]) //比较组合数高位
return rk[i] < rk[j];
else { //比较组合数低位
int ri = i + k <= n ? rk[i + k] : -1;
int rj = j + k <= n ? rk[j + k] : -1;
return ri < rj;
}
}
void calc_sa() { //计算sa[](快速排序)
for (int i = 0; i <= n; i++) {
rk[i] = s[i]; //记录原始数值
sa[i] = i; //记录当前排序结果
}
for (k = 1; k <= n; k *= 2) { //每次递增2倍
sort(sa, sa + n, cmp_sa);
//因为rk[]存在相同数,所以需要上一轮rk[]才能比较(即cmp_sa里)
//所以不能直接赋给rk[],需要一个tmp[]周转
tmp[sa[0]] = 0;
for (int i = 0; i < n; i++) //sa[]倒推组合数记录在tmp[]
tmp[sa[i + 1]] = tmp[sa[i]] + (cmp_sa(sa[i], sa[i + 1]) ? 1 : 0);
for (int i = 0; i < n; i++)
rk[i] = tmp[i];
}
}
int main() {
memcpy(s, "aabab", 6);
n = strlen(s);
calc_sa();
for (int i = 0; i < n; i++)
cout << sa[i] << " ";
// 0 3 1 4 2
return 0;
}
除了直接用快排sort,还有一种更快的排序方式——基数排序,总复杂度只有
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),就是有题目卡这点时间,丧心病狂。
基数排序是先比较低位再比较高位,使用哈希的思路,对于该位相同的数字直接放到相应的格子里。如排序{82,43,67,52,91,40},先按个位排序得{40,91,82,52,43,67},再按十位排序得{40,43,52,67,82,91}以此类推。
| 格子 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 个位 | 40 | 91 | 82,52 | 43 | 67 | |||||
| 十位 | 40,43 | 52 | 67 | 82 | 91 |
模板:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 200005;
char s[maxn];
int sa[maxn], rk[maxn];
int cnt[maxn], t1[maxn], t2[maxn];
int n, k;
void calc_sa() { //计算sa[](基数排序)
int m = 127; //ASCLL范围
int i, * x = t1, * y = t2;
for (i = 0; i < m; i++)cnt[i] = 0;
for (i = 0; i < n; i++)cnt[x[i] = s[i]]++;
for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
for (i = n - 1; i >= 0; i--)sa[--cnt[x[i]]] = i;
for (k = 1; k <= n; k *= 2) {
int p = 0; //利用长度k的排序结果对长度2k的排序
for (i = n - k; i < n; i++)y[p++] = i;
for (i = 0; i < n; i++)
if (sa[i] >= k)y[p++] = sa[i] - k;
for (i = 0; i < m; i++)cnt[i] = 0;
for (i = 0; i < n; i++)cnt[x[y[i]]]++;
for (i = 1; i < m; i++)cnt[i] += cnt[i - 1];
for (i = n - 1; i >= 0; i--)sa[--cnt[x[y[i]]]] = y[i];
swap(x, y);
p = 1;
x[sa[0]] = 0;
for (i = 1; i < n; i++)
x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p