字符串-Manacher算法(你知道马拉车算法吗?)
Posted 吾仄lo咚锵
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了字符串-Manacher算法(你知道马拉车算法吗?)相关的知识,希望对你有一定的参考价值。

原理
马拉车算法当然不是马拉着车的奇奇怪怪的东西,是Manacher’s Algorithm的音译。
Manacher’s Algorithm马拉车算法是一种可以在
O
(
n
)
O(n)
O(n)线性时间内求最长回文子串的算法(Manacher是人名,发明者)。所谓的回文也就是正读反读都是一样的,比如
n
o
o
n
noon
noon、
l
e
v
e
l
level
level,那在一个字符串中找最长的回文子串,一般使用中心扩展法,也就是枚举每一个字符为对称中心,然后向左右延伸并判断是否相等,但这种方法的时间复杂度是
O
(
n
2
)
O(n^2)
O(n2)。
分析中心扩展法效率差的原因,是因为它做了大量重复计算,比如字符串 a a a a a a a a a aaaaaaaaa aaaaaaaaa、 a b a b a b a abababa abababa,也就是最坏的情况——各个回文子串相互重叠。而马拉车算法则通过一些空间记录和回文对称的特点来避免这种重复计算。
奇偶问题
首先需要解决字符串长度奇偶时,对称中心不一致的问题。如串 a b a aba aba和 a b b a abba abba都是回文串,但是它们的对称中心分别是不一致的,前者是 b b b,后者是位于 b b b中间。
我们在每个字符前后加上一个’#‘符,并且为了后续不越界和求原下标方便,我们让新字符串
t
t
t的下标从1开始,即下标0处也赋’#’。这样处理后字符串的长度就都是奇数了,对称中心自然也都是二分之一处的字符,不会再是位于两字符中间的情况。
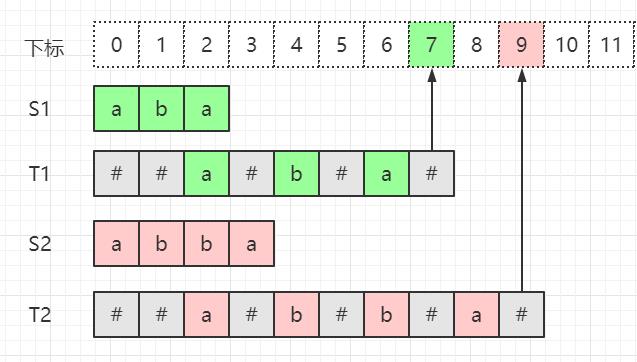
p[]数组
现在我们引用一个数组p[]来表示中心扩展的最大长度,而它就是去掉’#'后原回文子串的长度,也就是我们求的答案。
以字符串 a b a b a a b ababaab ababaab为例,通过 P P P的下标 i i i减去 P [ i ] P[i] P[i]再除以 2 2 2就能求出原回文子串,如下标 8 8 8处 P [ 8 ] = 3 P[8]=3 P[8]=3, ( 8 − 3 ) / 2 = 2 (8-3)/2=2 (8−3)/2=2,即在原串 S S S中下标 2 2 2开始长度为 3 3 3的子串是一个回文子串( a b a aba aba)。
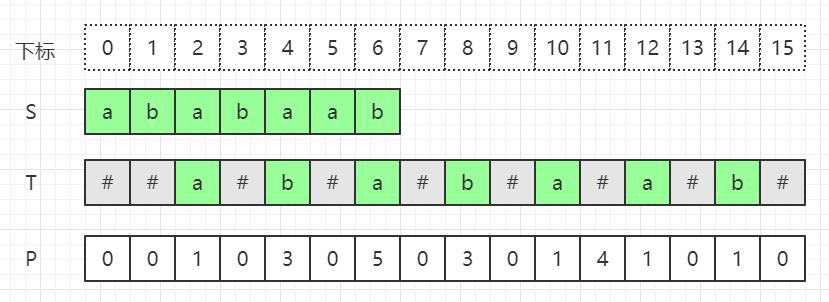
马拉车求p[]
前面都是准备工作,下面才是马拉车的核心算法,它充分利用了回文的对称性,比如说对于回文串
a
b
a
b
a
ababa
ababa,不难发现它的
p
[
]
p[]
p[]数组也是关于中心对称的,如下图:

但这只限于回文串中可以这样直接镜像,还需要推导至一般情况,仍以串
a
b
a
b
a
a
b
ababaab
ababaab为例。
设
m
i
d
mid
mid为对称中心,
r
r
r表示回文串的右边半径(
r
=
m
i
d
+
p
[
i
]
r=mid+p[i]
r=mid+p[i]),下标
i
i
i即当前要求的
p
[
i
]
p[i]
p[i],下标
j
j
j表示
i
i
i关于中心
m
i
d
mid
mid镜像对称的下标,分如下三种情况:
-
合法范围内
就是上面讨论的情形,直接赋值即可。
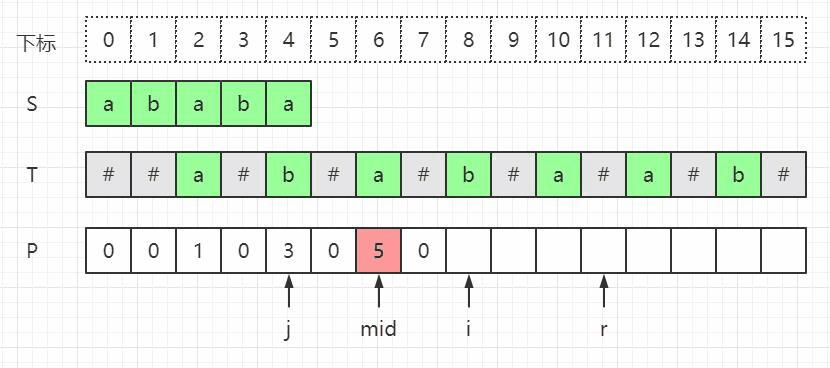
-
j j j遇到原字符串左边界
此时不能直接赋值,因为 j j j位置处是因为向左到尽头越界,而镜像处的 i i i向左没有越界,应该继续比较,即用中心扩展法。
虽然此处答案都是1,但 j j j是因为到了首字符‘#’必不相等,而 i i i是可以匹配的,只是此处 a a a和 b b b匹配失败。
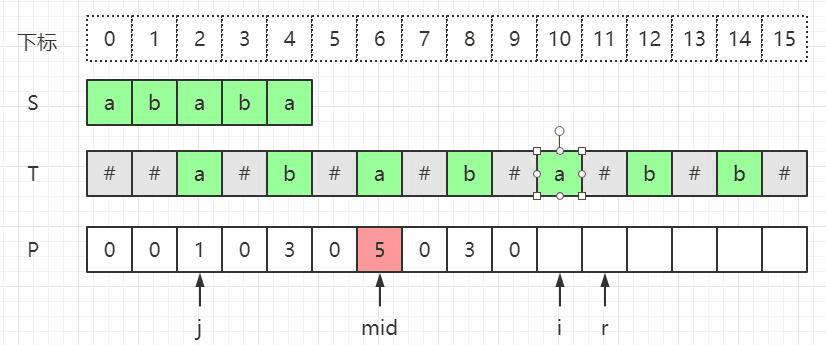
-
i i i>= r r r
同上面一样不能利用对称性了,将 p [ i ] p[i] p[i]置0,用中心扩展法。
同时注意更新 m i d mid mid和 r r r,也就是当更新 p [ i ] p[i] p[i]后,求出新的 r ( p [ i ] + i ) r(p[i]+i) r(p[i]+i),若大于旧的 r r r,就更新 m i d mid mid和 r r r,即设置当前点 i i i为新的对称中心。
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
模板
#include <iostream>
#include <string>
using namespace std;
const int maxn = 1000006;
int p[maxn];
string s, t;
int main() {
cin >> s;
int n = s.size();
t = "#";
for (int i = 0; i < n; i++) {
t += '#';
t += s[i];
}
t += '#';
int m = t.size();
int mid = 0, r = 0;
int len = 0, st = 0;//回文串长度和起始位置
for (int i = 1; i < m - 1; i++) {
int j = mid * 2 - i;
if (i < r) //右边半径内
p[i] = min(r - i, p[j]);//防止超出r
else p[i] = 0; //>=r情况
while (t[i + 1 + p[i]] == t[i - 1 - p[i]])
p[i]++; //中心扩展
if (i + p[i] > r) { //更新r
mid = i;
r = i + p[i];
}
if (p[i] > len) { //顺便更新答案
len = p[i];
st = (i - p[i]) / 2;
}
}
cout << len << "\\n" << s.substr(st, len);
return 0;
}
注意时间复杂度是 O ( n ) O(n) O(n),当里面的while循环中心扩展后,下次循环是不会再访问到这些节点的,会直接用对称性。
例题
P3805 【模板】manacher算法
题目描述
给出一个只由小写英文字符 \\texttt a,\\texttt b,\\texttt c,\\ldots\\texttt y,\\texttt za,b,c,…y,z 组成的字符串 SS ,求 SS 中最长回文串的长度 。
字符串长度为 nn。
输入格式
一行小写英文字符 \\texttt a,\\texttt b,\\texttt c,\\ldots\\texttt y,\\texttt za,b,c,…y,z 组成的字符串 SS。
输出格式
一个整数表示答案。
输入输出样例
输入 #1
aaa
输出 #1
3
说明/提示
1≤n≤1.1×107
#include <iostream>
#include <string>
using namespace std;
const int maxn=32000007;
int p[maxn]={0};
string s,t;
int main(){
cin>>s;
int n=s.size();
t="#";
for(int i=0;i<n;i++){
t+='#';
t+=s[i];
}
t+='#';
int m=t.size();
int mid=0,r=0,ans=0;
for(int i=1;i<m-1;i++){
int j=mid*2-i;
if(i<r)
p[i]=min(r-i,p[j]);
while(t[i+1+p[i]]==t[i-1-p[i]])
p[i]++;
if(i+p[i]>r){
mid=i;
r=i+p[i];
}
if(p[i]>ans)ans=p[i];
}
cout<<ans;
return 0;
}
P1659 拉拉队排练
题目描述
艾利斯顿商学院篮球队要参加一年一度的市篮球比赛了。拉拉队是篮球比赛的一个看点,好的拉拉队往往能帮助球队增加士气,赢得最终的比赛。所以作为拉拉队队长的楚雨荨同学知道,帮助篮球队训练好拉拉队有多么的重要。
拉拉队的选拔工作已经结束,在雨荨和校长的挑选下,n位集优秀的身材、舞技于一体的美女从众多报名的女生中脱颖而出。这些女生将随着篮球队的小伙子们一起,和对手抗衡,为艾利斯顿篮球队加油助威。
一个阳光明媚的早晨,雨荨带领拉拉队的队员们开始了排练。n个女生从左到右排成一行,每个人手中都举了一个写有26个小写字母中的某一个的牌子,在比赛的时候挥舞,为小伙子们呐喊、加油。
雨荨发现,如果连续的一段女生,有奇数个,并且他们手中的牌子所写的字母,从左到右和从右到左读起来一样,那么这一段女生就被称作和谐小群体。
现在雨荨想找出所有和谐小群体,并且按照女生的个数降序排序之后,前K个和谐小群体的女生个数的乘积是多少。由于答案可能很大,雨荨只要你告诉她,答案除以19930726的余数是多少就行了。
输入格式
输入为标准输入。
第一行为两个正整数n和K,代表的东西在题目描述中已经叙述。
接下来一行为n个字符,代表从左到右女生拿的牌子上写的字母。
输出格式
输出为标准输出。
输出一个整数,代表题目描述中所写的乘积除以19930726的余数,如果总的和谐小群体个数小于K,输出一个整数-1。
输入输出样例
输入 #1
5 3
ababa
输出 #1
45
说明/提示
样例说明
和谐小群体女生所拿牌子上写的字母从左到右按照女生个数降序排序后为ababa, aba, aba, bab, a, a, a, b, b,前三个长度的乘积为 。
跑一遍马拉车,并使用cnt[]数组记录回文串长度对应数量,过滤奇数的,从大往小循环即可,另外注意直接乘会超时,用快速幂。
#include <iostream>
#include <string>
using namespace std;
const int maxn = 2000006;
const int mod = 19930726;
typedef long long ll;
int p[maxn], cnt[maxn];
string s, t;
ll n, k;
ll qpow(ll x, ll y) {
ll res = 1;
while (y) {
if (y & 1)res = (res * x) % mod;
x = (x * x) % mod;
y >>= 1;
}
return res;
}
int main() {
cin >> n >> k >> s;
t = "#";
for (int i = 0; i < n; i++) {
t += '#';
t += s[i];
}
t += '#';
ll m = t.size();
int mid = 0, r = 0;
for (int i = 1; i < m - 1; i++) {
int j = mid * 2 - i;
if (i < r)
p[i] = min(r - i, p[j]);
else p[i] = 0;
while (t[i + 1 + p[i]] == t[i - 1 - p[i]])
p[i]++;
if (i + p[i] > r) {
mid = i;
r = i + p[i];
}
if (p[i] % 2)cnt[p[i]]++;
}
ll sum = 0, ans = 1;
for (int i = n; i >= 1; i--) {
if (i % 2 == 0)continue;
sum += cnt[i];
ll cur = min(sum, k);
k -= sum;
ans = (ans * qpow(i, cur)) % mod;
if (k < 0)break;
}
if (k > 0)ans = -1;
cout << ans;
return 0;
}
以上是关于字符串-Manacher算法(你知道马拉车算法吗?)的主要内容,如果未能解决你的问题,请参考以下文章