面试官：为何Redis使用跳表而非红黑树实现SortedSet？

Posted 2021-09-16 JavaEdge.

知道跳表（Skip List）是在看关于Redis的书的时候，Redis中的有序集合使用了跳表数据结构。接着就查了一些博客，来学习一下跳表。后面会使用Java代码来简单实现跳表。

什么是跳表

跳表由William Pugh发明，他在论文《Skip lists: a probabilistic alternative to balanced trees》中详细介绍了跳表的数据结构和插入删除等操作，论文是这么介绍跳表的：

Skip lists are a data structure that can be used in place of balanced trees.Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

也就是说，跳表可以用来替代红黑树，使用概率均衡技术，使得插入、删除操作更简单、更快。先来看论文里的一张图：

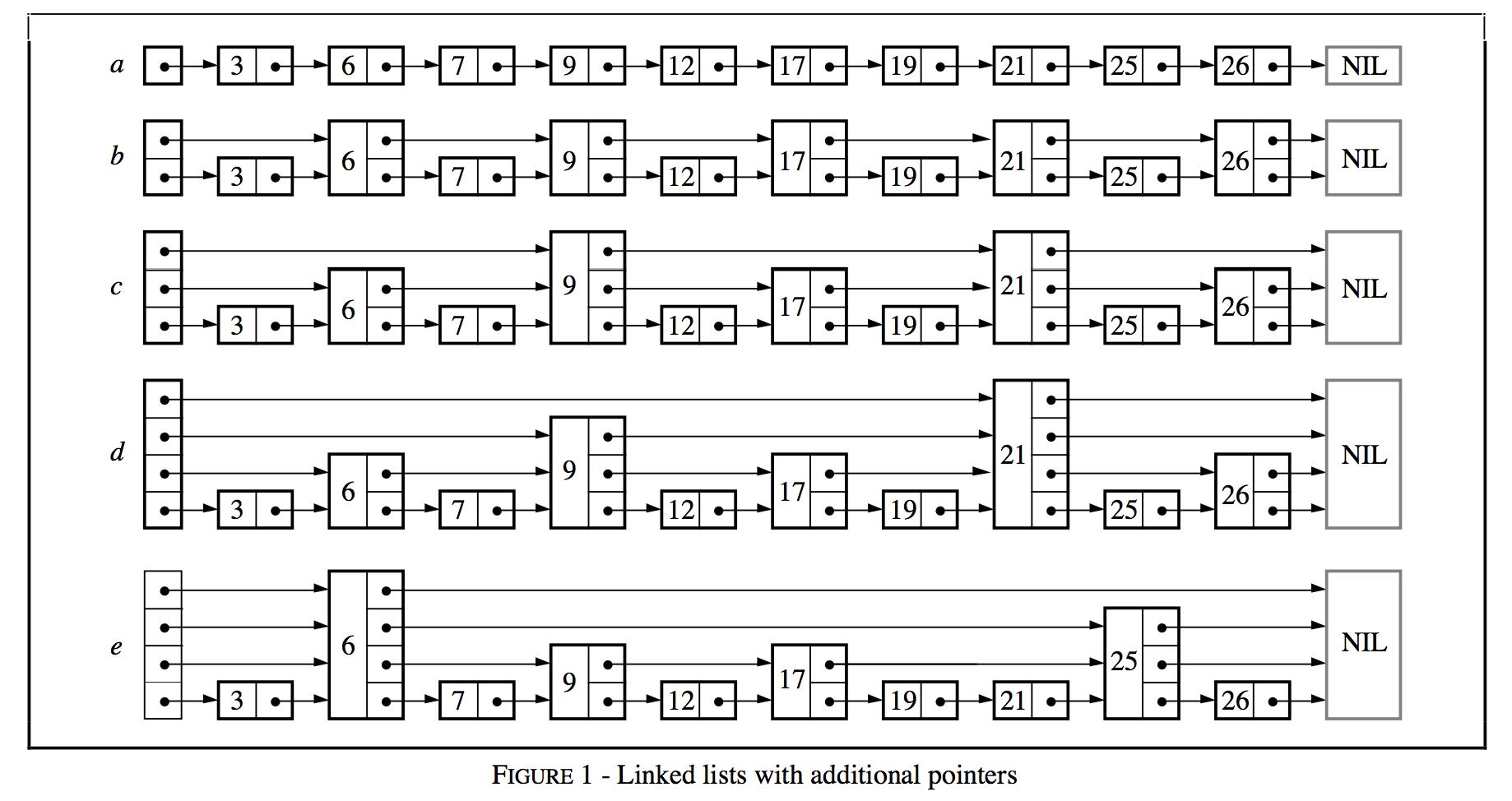
观察上图

• a：已排好序的链表，查找一个结点最多需要比较N个结点。
• b：每隔2个结点增加一个指针，指向该结点间距为2的后续结点，那么查找一个结点最多需要比较ceil(N/2)+1个结点。
• c，每隔4个结点增加一个指针，指向该结点间距为4的后续结点，那么查找一个结点最多需要比较ceil(N/4)+1个结点。
• 若每第2^i 个结点都有一个指向间距为 2^i的后续结点的指针，这样不断增加指针，比较次数会降为log(N)。这样的话，搜索会很快，但插入和删除会很困难。

一个拥有k个指针的结点称为一个k层结点（level k node）。按照上面的逻辑，50%的结点为1层，25%的结点为2层，12.5%的结点为3层…如果每个结点的层数随机选取，但仍服从这样的分布呢（上图e，对比上图d）？

使一个k层结点的第i个指针指向第i层的下一个结点，而不是它后面的第2^(i-1)个结点，那么结点的插入和删除只需要原地修改操作；一个结点的层数，是在它被插入的时候随机选取的，并且永不改变。因为这样的数据结构是基于链表的，并且额外的指针会跳过中间结点，所以作者称之为跳表（Skip Lists）。

二分查找底层依赖数组随机访问的特性，所以只能用数组实现。若数据存储在链表，就没法用二分搜索了？

其实只需稍微改造下链表，就能支持类似“二分”的搜索算法，即跳表（Skip list），支持快速的新增、删除、搜索操作。

Redis中的有序集合（Sorted Set）就是用跳表实现的。我们知道红黑树也能实现快速的插入、删除和查找操作。那Redis 为何不选择红黑树来实现呢？

跳表的意义究竟在于何处？

单链表即使存储的数据有序，若搜索某数据，也只能从头到尾遍历，搜索效率很低，平均时间复杂度是O(n)。

追求极致的程序员就开始想了，那这该如何提高链表结构的搜索效率呢？
若如下图，对链表建立一级“索引”，每两个结点提取一个结点到上一级，把抽出来的那级叫作索引或索引层。图中的down表示down指针，指向下一级结点。

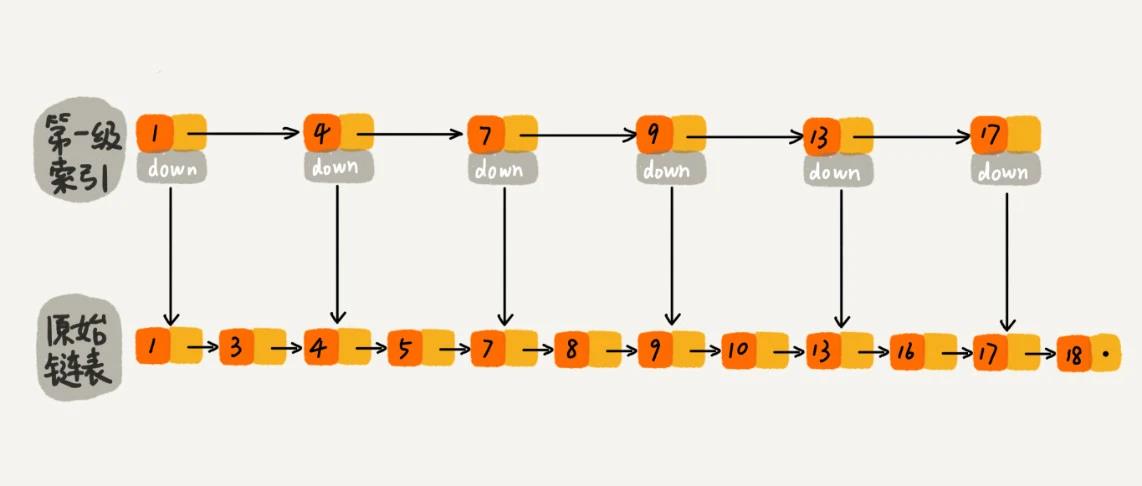
比如要搜索16：

• 先遍历索引层，当遍历到索引层的13时，发现下一个结点是17，说明目标结点位于这俩结点中间
• 然后通过down指针，下降到原始链表层，继续遍历
  此时只需再遍历2个结点，即可找到16！

原先单链表结构需遍历10个结点，现在只需遍历7个结点即可。可见，加一层索引，所需遍历的结点个数就减少了，搜索效率提升。

若再加层索引，搜索效率是不是更高？于是每两个结点再抽出一个结点到第二级索引。现在搜索16，只需遍历6个结点了！

这里数据量不大，可能你也没感觉到搜索效率ROI高吗。

那数据量就变大一点，现有一64结点链表，给它建立五级的索引。

原来没有索引时，单链表搜索62需遍历62个结点！
现在呢？只需遍历11个！所以你现在能体会到了，当链表长度n很大时，建立索引后，搜索性能显著提升。

这种有多级索引的，可以提高查询效率的链表就是最近火遍面试圈的跳表。
作为严谨的程序员，我们又开始好奇了

跳表的搜索时间复杂度

我们都知道单链表搜索时间复杂度O(n)，那如此快的跳表呢？

若链表有n个结点，会有多少级索引呢？假设每两个结点抽出一个结点作为上级索引，则：

• 第一级索引结点个数是n/2
• 第二级n/4
• 第三级n/8
• …
• 第k级就是n/(2^k)

假设索引有h级，最高级索引有2个结点，可得：

n/(2h) = 2

所以：

h = log2n-1

若包含原始链表这一层，整个跳表的高度就是log2 n。我们在跳表中查询某个数据的时候，如果每一层都要遍历m个结点，那在跳表中查询一个数据的时间复杂度就是O(m*logn)。

那这个m的值是多少呢？按照前面这种索引结构，我们每一级索引都最多只需要遍历3个结点，也就是说m=3，为什么是3呢？我来解释一下。

假设我们要查找的数据是x，在第k级索引中，我们遍历到y结点之后，发现x大于y，小于后面的结点z，所以我们通过y的down指针，从第k级索引下降到第k-1级索引。在第k-1级索引中，y和z之间只有3个结点（包含y和z），所以，我们在K-1级索引中最多只需要遍历3个结点，依次类推，每一级索引都最多只需要遍历3个结点。

通过上面的分析，我们得到m=3，所以在跳表中查询任意数据的时间复杂度就是O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说，我们其实是基于单链表实现了二分查找，是不是很神奇？不过，天下没有免费的午餐，这种查询效率的提升，前提是建立了很多级索引，也就是我们在第6节讲过的空间换时间的设计思路。

跳表是不是很费内存？

由于跳表要存储多级索引，势必比单链表消耗更多存储空间。那到底是多少呢？
若原始链表大小为n：

• 第一级索引大约有n/2个结点
• 第二级索引大约有n/4个结点
• …
• 最后一级2个结点

多级结点数的总和就是：

n/2+n/4+n/8…+8+4+2=n-2

所以空间复杂度是O(n)。这个量还是挺大的，能否再稍微降低索引占用的内存空间呢？
若每三五个结点才抽取一个到上级索引呢？

• 第一级索引需要大约n/3个结点
• 第二级索引需要大约n/9个结点
• 每往上一级，索引结点个数都除以3

假设最高级索引结点个数为1，总索引结点数：

n/3+n/9+n/27+…+9+3+1=n/2

尽管空间复杂度还是O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半的索引结点存储空间。

我们大可不必过分在意索引占用的额外空间，实际开发中，原始链表中存储的有可能是很大的对象，而索引结点只需存储关键值和几个指针，无需存储对象，所以当对象比索引结点大很多时，那索引占用的额外空间可忽略。

插入和删除的时间复杂度

插入

在跳表中插入一个数据，只需O(logn)时间复杂度。
单链表中，一旦定位好要插入的位置，插入的时间复杂度是O(1)。但这里为了保证原始链表中数据的有序性，要先找到插入位置，所以这个过程中的查找操作比较耗时。

单纯的单链表，需遍历每个结点以找到插入的位置。但跳表搜索某结点的的时间复杂度是O(logn)，所以搜索某数据应插入的位置的时间复杂度也是O(logn)。

删除

如果这个结点在索引中也有出现，除了要删除原始链表的结点，还要删除索引中的。
因为单链表删除操作需拿到要删除结点的前驱结点，然后通过指针完成删除。所以查找要删除结点时，一定要获取前驱结点。若是双向链表，就没这个问题了。

跳表索引动态更新

当不停往跳表插入数据时，若不更新索引，就可能出现某2个索引结点之间数据非常多。极端情况下，跳表还会退化成单链表。

作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。

像红黑树、AVL树这样的平衡二叉树通过左右旋保持左右子树的大小平衡，而跳表是通过随机函数维护前面提到的“平衡性”。

往跳表插入数据时，可以选择同时将这个数据插入到部分索引层中。

那如何选择加入哪些索引层呢？

通过一个随机函数决定将这个结点插入到哪几级索引中，比如随机函数生成了值K，那就把这个结点添加到第一级到第K级这K级索引中。

为何Redis要用跳表来实现有序集合，而不是红黑树？

Redis中的有序集合支持的核心操作主要支持：

• 插入一个数据
• 删除一个数据
• 查找一个数据
• 迭代输出有序序列
  以上操作，红黑树也能完成，时间复杂度跟跳表一样。
• 按照区间查找数据
  红黑树的效率低于跳表。跳表可以做到O(logn)定位区间的起点，然后在原始链表顺序往后遍历即可。

除了性能，还有其它原因：

• 代码实现比红黑树好懂、好写多了，因为简单就代表可读性好，不易出错
• 跳表更灵活，可通过改变索引构建策略，有效平衡执行效率和内存消耗

因为红黑树比跳表诞生更早，很多编程语言中的Map类型（比如JDK 的 HashMap）都是通过红黑树实现的。业务开发时，直接从JDK拿来用，但跳表没有一个现成的实现，只能自己实现。

跳表的代码实现（Java 版）

数据结构定义

表中的元素使用结点来表示，结点的层数在它被插入时随机计算决定（与表中已有结点数目无关）。
一个i层的结点有i个前向指针（java中使用结点对象数组forward来表示），索引为从1到i。用MaxLevel来记录跳表的最大层数。
跳表的层数为当前所有结点中的最大层数（如果list为空，则层数为1）。
列表头header拥有从1到MaxLevel的前向指针：

public class SkipList<T> {

    // 最高层数
    private final int MAX_LEVEL;
    // 当前层数
    private int listLevel;
    // 表头
    private SkipListNode<T> listHead;
    // 表尾
    private SkipListNode<T> NIL;
    // 生成randomLevel用到的概率值
    private final double P;
    // 论文里给出的最佳概率值
    private static final double OPTIMAL_P = 0.25;
    
    public SkipList() {
        // 0.25, 15
        this(OPTIMAL_P, (int)Math.ceil(Math.log(Integer.MAX_VALUE) / Math.log(1 / OPTIMAL_P)) - 1);
    }

    public SkipList(double probability, int maxLevel) {
        P = probability;
        MAX_LEVEL = maxLevel;

        listLevel = 1;
        listHead = new SkipListNode<T>(Integer.MIN_VALUE, null, maxLevel);
        NIL = new SkipListNode<T>(Integer.MAX_VALUE, null, maxLevel);
        for (int i = listHead.forward.length - 1; i >= 0; i--) {
            listHead.forward[i] = NIL;
        }
    }

    // 内部类
    class SkipListNode<T> {
        int key;
        T value;
        SkipListNode[] forward;
        
        public SkipListNode(int key, T value, int level) {
            this.key = key;
            this.value = value;
            this.forward = new SkipListNode[level];
        }
    }
}

搜索算法

按key搜索，找到返回该key对应的value，未找到则返回null。

通过遍历forward数组来需找特定的searchKey。假设skip list的key按照从小到大的顺序排列，那么从跳表的当前最高层listLevel开始寻找searchKey。在某一层找到一个非小于searchKey的结点后，跳到下一层继续找，直到最底层为止。那么根据最后搜索停止位置的下一个结点，就可以判断searchKey在不在跳表中。

• 在跳表中找8的过程：
  

插入和删除算法

都是通过查找与连接（search and splice）：

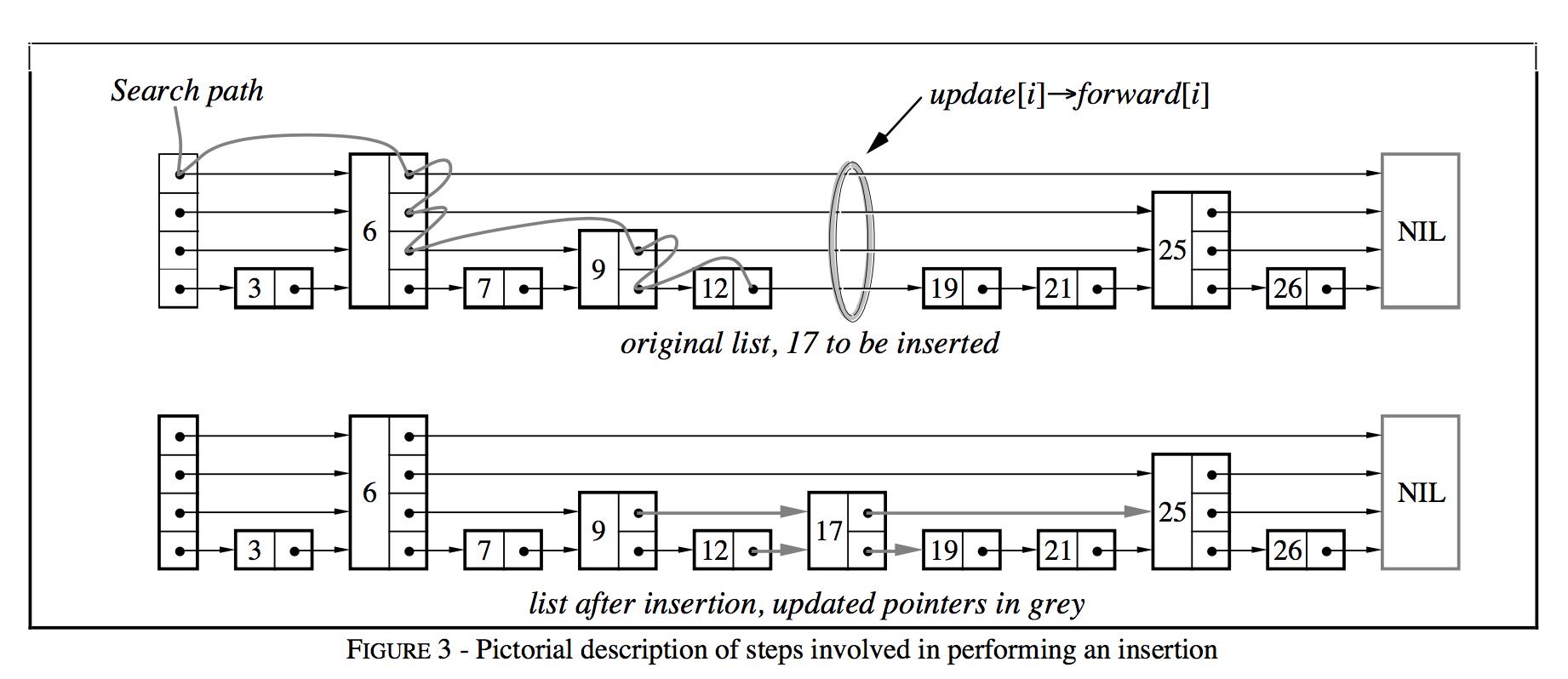
维护一个update数组，在搜索结束之后，update[i]保存的是待插入/删除结点在第i层的左侧结点。

插入

若key不存在，则插入该key与对应的value；若key存在，则更新value。

如果待插入的结点的层数高于跳表的当前层数listLevel，则更新listLevel。

选择待插入结点的层数randomLevel：

randomLevel只依赖于跳表的最高层数和概率值p。

另一种实现方法为，如果生成的randomLevel大于当前跳表的层数listLevel，那么将randomLevel设置为listLevel+1，这样方便以后的查找，在工程上是可以接受的，但同时也破坏了算法的随机性。

删除

删除特定的key与对应的value。如果待删除的结点为跳表中层数最高的结点，那么删除之后，要更新listLevel。

public class SkipList<T> {

    // 最高层数
    private final int MAX_LEVEL;
    // 当前层数
    private int listLevel;
    // 表头
    private SkipListNode<T> listHead;
    // 表尾
    private SkipListNode<T> NIL;
    // 生成randomLevel用到的概率值
    private final double P;
    // 论文里给出的最佳概率值
    private static final double OPTIMAL_P = 0.25;

    public SkipList() {
        // 0.25, 15
        this(OPTIMAL_P, (int)Math.ceil(Math.log(Integer.MAX_VALUE) / Math.log(1 / OPTIMAL_P)) - 1);
    }

    public SkipList(double probability, int maxLevel) {
        P = probability;
        MAX_LEVEL = maxLevel;

        listLevel = 1;
        listHead = new SkipListNode<T>(Integer.MIN_VALUE, null, maxLevel);
        NIL = new SkipListNode<T>(Integer.MAX_VALUE, null, maxLevel);
        for (int i = listHead.forward.length - 1; i >= 0; i--) {
            listHead.forward[i] = NIL;
        }
    }

    // 内部类
    class SkipListNode<T> {
        int key;
        T value;
        SkipListNode[] forward;
        
        public SkipListNode(int key, T value, int level) {
            this.key = key;
            this.value = value;
            this.forward = new SkipListNode[level];
        }
    }

    public T search(int searchKey) {
        SkipListNode<T> curNode = listHead;

        for (int i = listLevel; i > 0; i--) {
            while (curNode.forward[i].key < searchKey) {
                curNode = curNode.forward[i];
            }
        }

        if (curNode.key == searchKey) {
            return curNode.value;
        } else {
            return null;
        }
    }

    public void insert(int searchKey, T newValue) {
        SkipListNode<T>[] update = new SkipListNode[MAX_LEVEL];
        SkipListNode<T> curNode = listHead;

        for (int i = listLevel - 1; i >= 0; i--) {
            while (curNode.forward[i].key < searchKey) {
                curNode = curNode.forward[i];
            }
            // curNode.key < searchKey <= curNode.forward[i].key
            update[i] = curNode;
        }

        curNode = curNode.forward[0];

        if (curNode.key == searchKey) {
            curNode.value = newValue;
        } else {
            int lvl = randomLevel();

            if (listLevel < lvl) {
                for (int i = listLevel; i < lvl; i++) {
                    update[i] = listHead;
                }
                listLevel = lvl;
            }

            SkipListNode<T> newNode = new SkipListNode<T>(searchKey, newValue, lvl);

            for (int i = 0; i < lvl; i++) {
                newNode.forward[i] = update[i].forward[i];
                update[i].forward[i] = newNode;
            }
        }
    }

    public void delete(int searchKey) {
        SkipListNode<T>[] update = new SkipListNode[MAX_LEVEL];
        SkipListNode<T> curNode = listHead;

        for (int i = listLevel - 1; i >= 0; i--) {
            while (curNode.forward[i].key < searchKey) {
                curNode = curNode.forward[i];
            }
            // curNode.key < searchKey <= curNode.forward[i].key
            update[i] = curNode;
        }

        curNode = curNode.forward[0];

        if (curNode.key == searchKey) {
            for (int i = 0; i < listLevel; i++) {
                if (update[i].forward[i] != curNode) {
                    break;
                }
                update[i].forward[i] = curNode.forward[i];
            }

            while (listLevel > 0 && listHead.forward[listLevel - 1] == NIL) {
                listLevel--;
            }
        }
    }

    private int randomLevel() {
        int lvl = 1;
        while (lvl < MAX_LEVEL && Math.random() < P) {
            lvl++;
        }
        return lvl;
    }

    public void print() {
    for (int i = listLevel - 1; i >= 0; i--) {
            SkipListNode<T> curNode = listHead.forward[i];
            while (curNode != NIL) {
                System.out.print(curNode.key + "->");
                curNode = curNode.forward[i];
            }
            System.out.println("NIL");
        }
    }

    public static void main(String[] args) {
        SkipList<Integer> sl = new SkipList<Integer>();
        sl.insert(20, 20);
        sl.insert(5, 5);
        sl.insert(10, 10);
        sl.insert(1, 1);
        sl.insert(100, 100);
        sl.insert(80, 80);
        sl.insert(60, 60);
        sl.insert(30, 30);
        sl.print();
        System.out.println("---");
        sl.delete(20);
        sl.delete(100);
        sl.print();
    }
}