《画解数据结构》「快速排序」算法教程

Posted 2021-09-16 英雄哪里出来

本文已收录于专栏 🌳《画解数据结构》🌳

文章目录

• 零、📃前言
• 一、🎯简单释义
• 二、🧡核心思想
• 三、🔆动图演示
• 四、🌳算法前置
• 五、🥦算法描述
• 六、🧶算法分析
• 七、🧢优化方案
• 八、💙源码详解
• 九、💗代码验证

零、📃前言

  「 快速排序 」 是利用了 「分而治之 」 的思想，进行递归计算的排序算法，效率在众多排序算法中的佼佼者，一般也会出现在各种 「数据结构」 的教科书上。于是，我也来简单讲一讲。我会尽量做到「深入浅出」，让 90% 的 「零基础小白 」 也都能理解，真正做到 「让天下没有难学的算法」 。我知道这很难，但是我愿意尝试！我会尽量把文章写得有趣。

🔥让天下没有难学的算法🔥
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习，抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜

那么，我的教程和别人的教程有什么不同的地方呢？
  「第一步」简单释义： 我会简单解释一下这个算法的目的、思想、以及为什么叫这个名字以帮助记忆。
  「第二步」核心思想： 我会大致介绍一下这个算法的核心思想。
  「第三步」动图演示： 我会引入一个动图，并且用一个切实的例子展示一下算法执行的全过程。
  「第四步」算法前置： 在学习这个算法之前，我们需要学习的前置内容有哪些？这些内容是需要事先去攻克的。
  「第五步」算法描述： 细致的讲解整个算法的执行流程。
  「第六步」算法分析： 对算法的时间复杂度和空间复杂度进行一个详细的分析。
  「第七步」优化方案： 介绍一些可以优化的点。
  「第八步」代码实践： 用 C/C++ 来实现上述算法。
  「第九步」代码验证： 最后，我会推荐一些比较好用的在线评测系统来验证我们实现的算法的正确性。

一、🎯简单释义

1、算法目的

  将原本乱序的数组变成有序，可以是 「升序」 或者 「降序」 （为了描述统一，本文一律只讨论 「 升序」 的情况）。

2、算法思想

  随机找到一个位置，将比它小的数都放到它 「 左边 」，比它大的数都放到它「 右边 」，然后分别「 递归 」求解 「 左边 」和「 右边 」使得两边分别有序。

3、命名由来

  由于排序速度较快，故此命名 「 快速排序 」 。

二、🧡核心思想

• 「递归」：函数通过改变参数，自己调用自己。
• 「比较」：关系运算符 小于($<$) 的运用。
• 「分治」：意为分而治之，先分，再治。将问题拆分成两个小问题，分别去解决。

三、🔆动图演示

1、样例

8	5	6	4	3	7	10	2

• 初始情况下的数据如 图二-1-1 所示，基本属于乱序，纯随机出来的数据。

图二-1-1

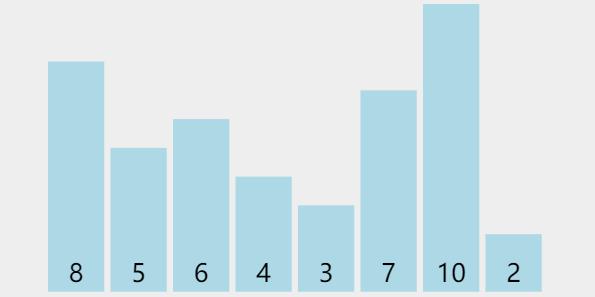
2、算法演示

• 接下来，我们来看下排序过程的动画演示。如 图二-2-1 所示：

图二-2-1

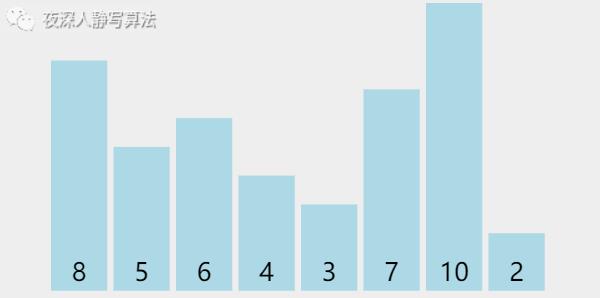
3、样例说明

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表随机选定的基准数
■ 的柱形	代表已经排序好的数
■ 的柱形	代表正在遍历比较的数
■ 的柱形	代表比基准数小的数
■ 的柱形	代表比基准数大的数

  我们发现，首先随机选择了一个 7 作为「 基准数 」，并且将它和最左边的数交换。然后往后依次遍历判断，小于 7 的数为 「 绿色 」 ，大于 7 的数为「 紫色 」，遍历完毕以后，将 7 和 「 下标最大的那个比 7 小的数 」交换位置，至此，7的左边位置上的数都小于它，右边位置上的数都大于它，左边和右边的数继续递归求解即可。

四、🌳算法前置

1、递归的实现

• 这个算法本身需要做一些「 递归 」计算，所以你至少需要知道「 递归 」 的含义，这里以 「 C语言 」 为例，来看下一个简单的「 递归 」是怎么写的。代码如下：

int sum(int n) {
    if(n <= 0) {
        return 0;
    } 
    return sum(n - 1) + n;
}

• 这就是一个经典的递归函数，求的是从 $1$ 到 $n$ 的和，那么我们把它想象成 $1$ 到 $n-1$ 的和再加 $n$，而 $1$ 到 $n-1$ 的和为sum(n-1)，所以整个函数体就是两者之和，这里sum(n)调用sum(n-1)的过程就被称为「 递归 」。

2、比较的实现

• 「比较」两个元素的大小，可以采用关系运算符，本文我们需要排序的数组是按照 「升序」 排列的，所以用到的关系运算符是 「小于运算符（即 <）」 。
• 我们可以将两个数的「比较」写成一个函数smallerThan，以 「 C语言 」 为例，实现如下：

#define Type int
bool smallerThan(Type a, Type b) {
    return a < b;
}

• 其中Type代表数组元素的类型，可以是整数，也可以是浮点数，也可以是一个类的实例，这里我们统一用int来讲解，即 32位有符号整型。

3、分治的实现

• 所谓「分治」，就是把一个复杂的问题分成两个（或更多的相同或相似的）「 子问题 」，再把子问题分成更小的「 子问题 」……，直到最后子问题可以简单的直接求解，原问题的解即「 子问题 」的解的合并。
• 对于 「 快速排序 」 来说，我们选择一个基准数，将小于它的数都放到左边，大于它的数都放到它的右边，这个过程其实就是天然隔离了 左边的数 和 右边的数，使得两边的数 “分开”，这样就可以分开治理了。如下图所示：

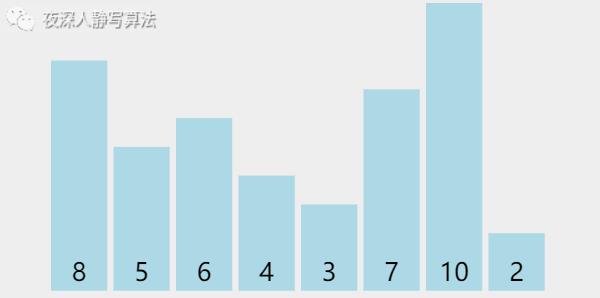
五、🥦算法描述

1、问题描述

  给定一个 $n$ 个元素的数组，数组下标从 $0$ 开始，采用「 快速排序 」将数组按照 「升序」排列。

2、算法过程

  整个算法的执行过程用 quickSort(a[], l, r)描述，代表 当前待排序数组 $a$，左区间下标 $l$，右区间下标 $r$，分以下几步：
  1） 随机生成基准点 $pivox=Partition(l,r)$；
  2） 递归调用quickSort(a[], l, pivox - 1)和quickSort(a[], pivox +1, r)；
  3） Partition(l, r)返回一个基准点，并且保证基准点左边的数都比它小，右边的数都比它大；Partition(l, r)称为分区。

六、🧶算法分析

1、时间复杂度

• 首先，我们分析跑一次分区的成本。
• 在实现分区Partition(l, r)中，只有一个 for循环遍历 $(r-l)$ 次。 由于 $r$ 可以和 $n-1$ 一样大，$i$ 可以低至 $0$，所以分区的时间复杂度是 $O(n)$。
• 类似于归并排序分析，快速排序的时间复杂度取决于分区被调用的次数。
• 当数组已经按照升序排列时，快速排序将达到最坏时间复杂度。总共 $n$ 次 分区，分区的时间计算如下：$$(n-1)+...+2+1=\frac{n(n-1)}{2}$$
• 总的时间复杂度为：$O(n^2)$
• 当分区总是将数组分成两个相等的一半时，就会发生快速排序的最佳情况，如归并排序。当发生这种情况时，递归的深度只有 $O(lo{g}_{2}n)$。总的时间复杂度为 $O(nlo{g}_{2}n)$。

2、空间复杂度

• 由于归并排序在归并过程中需要额外的一个「 辅助数组 」，并且最大长度为原数组长度，所以「 归并排序 」的空间复杂度为 $O(n)$。

七、🧢优化方案

  「 快速排序 」在众多排序算法中效率较高，平均时间复杂度为 $O(nlo{g}_{2}n)$。但当完全有序时，最坏时间复杂度达到最坏情况 $O(n^2)$。
   所以每次在选择基准数的时候，我们可以尝试用随机的方式选取，这就是 「 随机快速排序 」。
  想象一下在随机化版本的快速排序中，随机化数据透视选择，我们不会总是得到 $0$，$1$ 和 $n-1$ 这种非常差的分割。所以不会出现上文提到的问题。

八、💙源码详解

1、快速排序实现1

#include <stdio.h>
#include <malloc.h>
 
#define maxn 1000001

int a[maxn];

void Input(int n, int *a) {
    for(int i = 0; i < n; ++i) {
        scanf("%d", &a[i]);
    }
}

void Output(int n, int *a) {
    for(int i = 0; i < n; ++i) {
        if(i)
            printf(" ");
        printf("%d", a[i]);
    }
    puts("");
}

void Swap(int *a, int *b) {
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

int Partition(int a[], int l, int r){
    int i, j, pivox; 
    int idx = l + rand() % (r - l + 1);        // (1) 
    pivox = a[idx];                            // (2) 
    Swap(&a[l], &a[idx]);                      // (3) 
    i = j = l + 1;                             // (4) 
                                               // 
    while( i <= r ) {                          // (5) 
        if(a[i] < pivox) {                     // (6) 
            Swap(&a[i], &a[j]);                
            ++j;                               
        }
        ++i;                                   // (7) 
    }
    Swap(&a[l], &a[j-1]);                      // (8) 
    return j-1;
}


//递归进行划分
void QuickSort(int a[], int l, int r){
    if(l < r){
        int mid = Partition(a, l, r);
        QuickSort(a, l, mid-1);
        QuickSort(a, mid+1, r);
    }
}

int main() {
    int n;
    while(scanf("%d", &n) != EOF) {
        Input(n, a);
        QuickSort(a, 0, n-1);
        Output(n, a);
    }
    return 0;
} 

• $(1)$ 随机选择一个基准；
• $(2)$ pivox 代表基准值；
• $(3)$ 将基准和最左边的值交换；
• $(4)$ $i$ 和 $j$ 是两个同步指针，都从 $l+1$ 开始；$j-1$ 以后的数都是大于等于 基准值 的；
• $(5)$ 开始遍历整个排序区间，$i$ 一定比 $j$ 走的快，当 $i$ 到达最右边的位置时，遍历结束；
• $(6)$ 如果比基准值小的，交换 $a[i]$ 和 $a[j]$，并且自增 $j$ ；
• $(7)$ 每次遍历 $i$ 都需要自增；
• $(8)$ 第 $j$ 个元素以后都是不比基准值小的元素 ；

2、快速排序实现2

#include <stdio.h>
#include <malloc.h>
 
#define maxn 1000001

int a[maxn《画解数据结构》「希尔排序」算法教程

 ❤️五万字《十大排序算法》动图讲解❤️(建议收藏)
 ❤️五万字《十大排序算法》动图讲解❤️(建议收藏)
 ❤️六万字《算法和数据结构》之《画解数据结构》总纲，算法零基础教程❤️(建议收藏)
 ❤️六万字《算法和数据结构》之《画解数据结构》总纲，算法零基础教程❤️(建议收藏)
 万字总结画解八大排序算法