模式匹配----KMP算法

Posted 2021-09-16 可乐不解渴

眼睛为她下着雨，心却为她打着伞、

在上篇中，我们讲到了BF暴力模式匹配算法。下面我们将讲述BF算法的优化版本算法KMP算法。

🎃KMP

定义

我们知道BF算法效率低的原因就是要回溯，即在匹配失败后，子串回溯到0，主串回溯到本趟匹配开始的下一个位置。而在KMP算法中，当我们匹配失败了，主串是不进行回溯，一直回溯我们的匹配模式子串。

• 假设现在主串S匹配到 i 位置，模式串P匹配到 j 位置
  • 如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；
  • 如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位，移动到j移动到next[j]。之后我们可以写出如下代码：

int KMP(string str, string sub, size_t position)
{
    int strlen = (int)str.size();
    int sublen = (int)sub.size();
    if (strlen == 0 || sublen == 0)
    {
        return -1;
    }
    if (position < 0 || position >= str.size())
    {
        return -1;
    }

    int i = (int)position;
    int j = 0;
    
    while (i < strlen && j < sublen)
    {
        if (j == -1 || str[i] == sub[j])
        {
            ++i;  //如果匹配，一起++
            ++j;
        }
        else //如果不匹配，则回溯倒next[j]的位置
        {
            j = next[j];
        }
    }
    //i-j得位置就是我们开始匹配的第一个字符的位置，j就等于我们的sublen
    if (j >= sublen)
    {
        return i - j;
    }
    //没有匹配返回-1
    else
    {
        return -1;
    }
}

在上面中我们会发现有一个next数组，而next数组中的每一个值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。
KMP的精髓就是next数组，也就是用next[j]=k;来表示，不同的j来对应一个k值，这个k就是你将来要移动到的j要移到(回溯)的位置。
而K的值是怎么求的呢？

• 规则：找到匹配成功的部分的两个相等的真子串(不包括自身),一个以下标0开始，另一个以j-1下标结尾。
• 不管什么数据的next数组的前两个数据都为next[0]=-1；next[1]=0;在这里，我们以下标来开始，而说到的第几个第几个是从1开始。

我们以abcabc为例，由于next[0]=-1；next[1]=0;是默认的，所以我们从j=2开始。

我们发现T[0]=‘a’, T[j-1]=‘c’，此时我们并没有找到两个相同的真子串，所以j所在的位置的k值为0，匹配失败后依旧回溯到0下标。

到了这里我们可以看到有两个匹配的真子串为a。

j走到末尾后，我们可以找到以a开始以b结尾的两个真子串为ab

既然我们知道了怎么手动求next数组，那下面我举几个例子大家来算一下。
示例：a b a b c a b c d a b c d e，求其next数组？

推导

我们假设next[i]=k是成立的，所以当我们next[i]==1时，我们就知道了k在那个位置，进而才有下面的推导过程。

那我们是不是可以得到T[0] ~ T[k-1] == [x] ~ T[i-1] , 但这个x是不确定的，但我们可以去推导得到它。从上面得到式子那我们进而可以得到：

• k-1-0 == i-1-x，x= i-k。
• T[0] ~ T[k-1] == [i-k] ~ T[i-1]

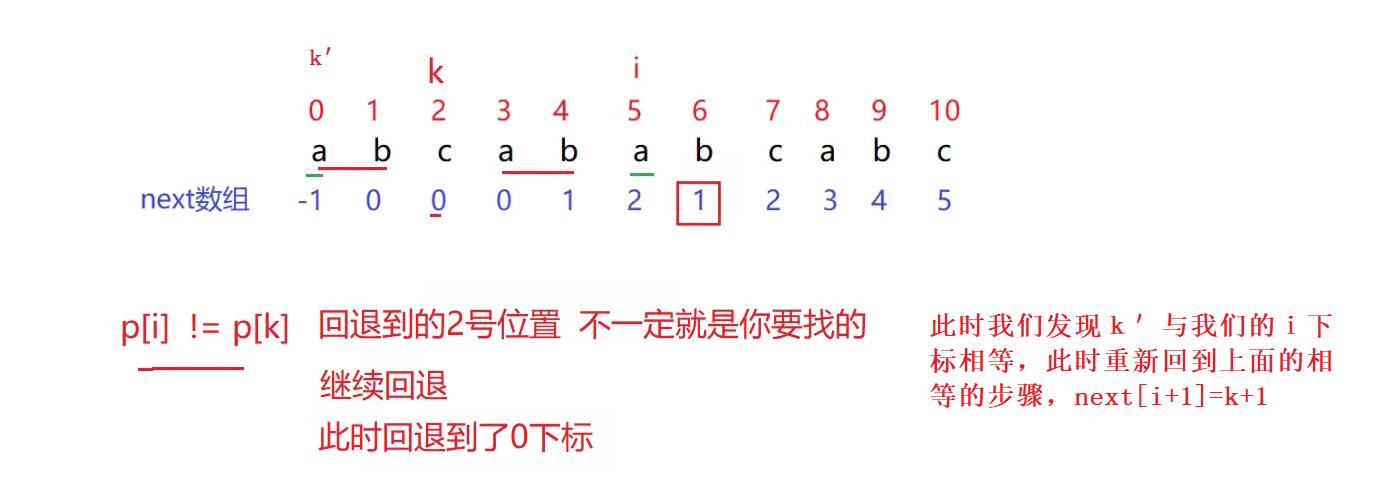
当T[i] == T[k] && T[0] ~ T[k-1] == [i-k] ~ T[i-1] 时，推导出next[i+1]的值。next[i+1]=k+1.

当T[i] !=T[k]时,不相等时，我们此时k就要回溯，回溯到相等的下标或者等于-1时停止。所以此时的next[i+1]=k+1。
本质就是一直回溯要找T[i] == T[k]。然后next[i+1]=k+1。

如果k=-1,就说明是走到了第一个元素还不匹配就是说明没有两个不相同的真子串的情况也让它进入上面的相等T[i] == T[k]的条件里。此时k==-1,那么next[i+1]=k+1，此时就让他从0开始匹配。

🎃代码实现

void GetNext(vector<int>& next,const string&sub)	//得到next数组
{
    next[0]=-1;
    next[1]=0;
    int k=0;
    int i=1;
    int sublen=sub.size();
    
    //为什么是小于sublen-1呢？这是因为当i+1>=sublen时访问数组时会越界
    while(i<sublen-1)
    {
    //这里next数组k回溯到等于-1时，此时就说明没有找到T[i] ==  T[k]，此时也让它进来，
    //表明该位置匹配失败后让它从头开始进行匹配
      if(k==-1||sub[i]==sub[k])
      {
        next[i+1]=k+1;    //如果sub[i]=sub[k],那么我们的next[i+1]=k+1
        ++i;  
        ++k;
        //下面这个if判断不要也行，只是在某些情况下可以优化next数组，让其只回溯一次
        if(sub[next[i]]==sub[i])  //优化next数组
        {
          next[i]=next[next[i]];
        }
      }
      else  //如果sub[i]!=sub[k],那么k我们就一直回溯
      {
        k=next[k];
      }
    }
}
int KMP(string str,string sub,size_t position)
{
	//这里的strlen是个变量不要和库函数里的strlen弄混淆。
	//这里我取的名字不太好，大家看的时候注意点
  int strlen=static_cast<int>(str.size());
  int sublen=static_cast<int>(sub.size());
  if(strlen==0||sublen==0)
  {
    return -1;
  }
  if(position<0||position>=str.size())
  {
    return -1;
  }

  int i=static_cast<int>position;
  int j=0;

  vector<int>next(sublen);
  //得到next数组，并将next数组优化
  GetNext(next,sub);
  
  while(i<strlen&&j<sublen)
  {
    //为什么当j==-1时，也要进来呢，这是因为next[0]==-1，j会一直回退。
    //j==-1了相当于第一个就匹配失败了，此时我们的主串S就得往下一个开始匹配
    //j由于是等于 -1的，它也++就变为 0了，重头开始匹配
    if(j==-1||str[i]==sub[j])	
    {
      ++i;  //如果匹配，一起++
      ++j;
    }
    else //如果不匹配，则回溯倒next[j]的位置
    {
      j=next[j];
    }
  }
  //i-j得位置就是我们开始匹配的第一个字符的位置，j就等于我们的sublen
  if(j>=sublen)
  {
    return i-j;
  }
  //没有匹配返回-1
  else
  {
    return -1;
  }
}

如果小伙伴还没看懂可以在评论区留言，我会在评论区给你解答！
如有错误之处还请各位指出！！！
那本篇文章就到这里啦，下次再见啦！