ABC215 D - Coprime 2（欧拉筛）

Posted 2021-09-16 live4m

题意：

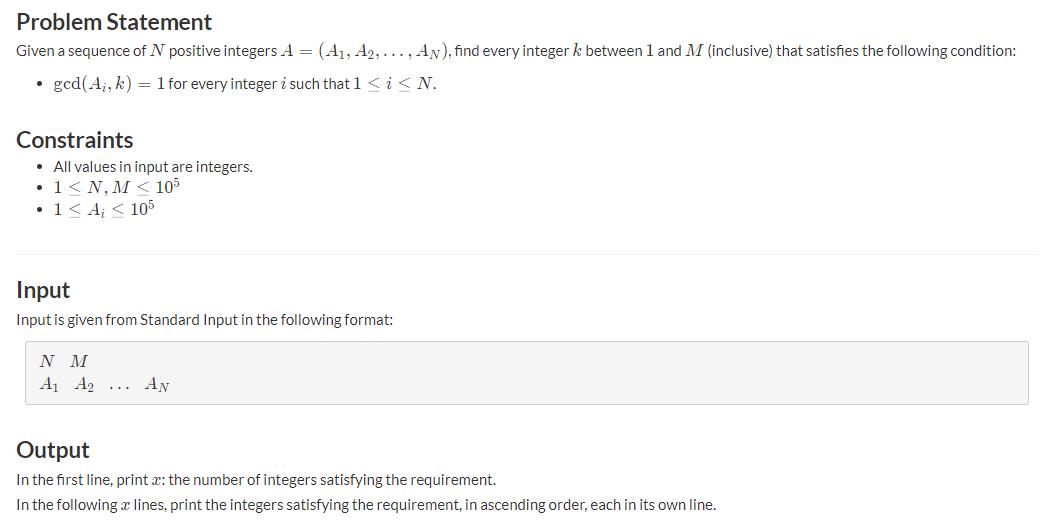
解法：

先质因子分解,将每个数>1的因子丢入set中,显然这些数是不能选的,
由于a[i]<=1e5,因此最后set的大小不会超过1e5,
对于set中的每一个元素x,显然x的倍数也是不能选的,因此将x的倍数筛掉.
那么剩下的未被筛的数就是答案了.
总复杂度O(n*log).

code：

#include<bits/stdc++.h>
#define int long long
#define PI pair<int,int>
using namespace std;
const int maxm=2e5+5;
int mark[maxm];
int a[maxm];
int n,m;
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>a[i];
    set<int>s;
    for(int i=1;i<=n;i++){
        for(int j=1;j*j<=a[i];j++){//记录所有因子
            if(a[i]%j==0){
                if(j>1)s.insert(j);
                if(a[i]/j>1)s.insert(a[i]/j);
            }
        }
    }
    for(auto i:s){
        for(int j=i;j<=m;j+=i){//所有因子的倍数也不能选
            mark[j]=1;
        }
    }
    vector<int>ans;
    for(int i=1;i<=m;i++){
        if(!mark[i])ans.push_back(i);
    }
    cout<<ans.size()<<endl;
    for(auto i:ans){
        cout<<i<<endl;
    }
}
signed main(){
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif // ONLINE_JUDGE
    ios::sync_with_stdio(0);cin.tie(0);
    solve();
    return 0;
}

---