卡尔曼滤波的应用

Posted 2021-09-15 三明治开发社区

上一篇微型巡逻摄像头—硬件方案中讲到平衡小车中使用MPU6050采集姿态数据，由于物理震动等原因，姿态数据波动较大，难以获取真正的姿态状态，无形中增加了后期平衡算法的难度。因此，我们需要先将MPU6050采集到的数据，进行数字滤波处理。

以角度采集为例，这里给大家推荐两种滤波算法，分别是卡尔曼滤波算法和一阶互补滤波算法，本篇主要介绍卡尔曼滤波在微型巡逻摄像头上的应用。

首先是加速度和角速度采集，如下

Gyro_X=(I2C_ReadOneByte(devAddr,MPU6050_RA_GYRO_XOUT_H)<<8)
+I2C_ReadOneByte(devAddr,MPU6050_RA_GYRO_XOUT_L);    //读取Y轴陀螺仪
​
Gyro_Z=(I2C_ReadOneByte(devAddr,MPU6050_RA_GYRO_ZOUT_H)<<8)
+I2C_ReadOneByte(devAddr,MPU6050_RA_GYRO_ZOUT_L);    //读取Z轴陀螺仪
​
Accel_Y=(I2C_ReadOneByte(devAddr,MPU6050_RA_ACCEL_YOUT_H)<<8)
+I2C_ReadOneByte(devAddr,MPU6050_RA_ACCEL_YOUT_L); //读取X轴加速度计
​
Accel_Z=(I2C_ReadOneByte(devAddr,MPU6050_RA_ACCEL_ZOUT_H)<<8)
+I2C_ReadOneByte(devAddr,MPU6050_RA_ACCEL_ZOUT_L); //读取Z轴加速度计
​
if(Gyro_X>32768)  Gyro_X-=65536;                       //数据类型转换  也可通过short强制类型转换
if(Gyro_Z>32768)  Gyro_Z-=65536;                       //数据类型转换
if(Accel_Y>32768) Accel_Y-=65536;                      //数据类型转换
if(Accel_Z>32768) Accel_Z-=65536;                      //数据类型转换
Gyro_X=Gyro_X-Gyro_X_OFFSET;
Gyro_Z=Gyro_Z-Gyro_Z_OFFSET;
Gyro_Balance=Gyro_X;                                  //更新平衡角速度
Accel_Angle=atan2(Accel_Y,Accel_Z)*180/PI;                 //计算倾角   

这里的Accel_Angle就是我们通过计算得出的原始角度值。

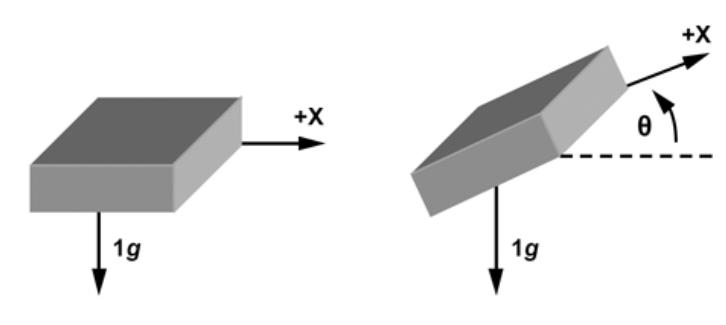
当然，也可以用公式Accel_Angle=arcsin(Accel_Y,Accel_G)*180/PI;

其中Accel_G=sqrt(pow(Accel_X, 2) + pow(Accel_Y, 2) + pow(Accel_Z, 2));

我们将设备静态放置，将数据绘制出来，如图

可以看到，原始数据波动特别大。

我们加入卡尔曼滤波，

Kalman_Filter(Accel_Angle,Gyro_X);

其中函数如下

void Kalman_Filter(float Accel,float Gyro)      
{
    angle+=(Gyro - Q_bias) * dt; //先验估计
    Pdot[0]=Q_angle - PP[0][1] - PP[1][0]; // Pk-先验估计误差协方差的微分
​
    Pdot[1]=-PP[1][1];
    Pdot[2]=-PP[1][1];
    Pdot[3]=Q_gyro;
    PP[0][0] += Pdot[0] * dt;   // Pk-先验估计误差协方差微分的积分
    PP[0][1] += Pdot[1] * dt;   // =先验估计误差协方差
    PP[1][0] += Pdot[2] * dt;
    PP[1][1] += Pdot[3] * dt;
        
    Angle_err = Accel - angle;  //zk-先验估计
    
    PCt_0 = C_0 * PP[0][0];
    PCt_1 = C_0 * PP[1][0];
    
    E = R_angle + C_0 * PCt_0;
    
    K_0 = PCt_0 / E;
    K_1 = PCt_1 / E;
    
    t_0 = PCt_0;
    t_1 = C_0 * PP[0][1];
​
    PP[0][0] -= K_0 * t_0;       //后验估计误差协方差
    PP[0][1] -= K_0 * t_1;
    PP[1][0] -= K_1 * t_0;
    PP[1][1] -= K_1 * t_1;
        
    angle   += K_0 * Angle_err;  //后验估计
    Q_bias  += K_1 * Angle_err;  //后验估计
    angle_dot   = Gyro - Q_bias;     //输出值(后验估计)的微分=角速度
}

将数据绘制出来，如图

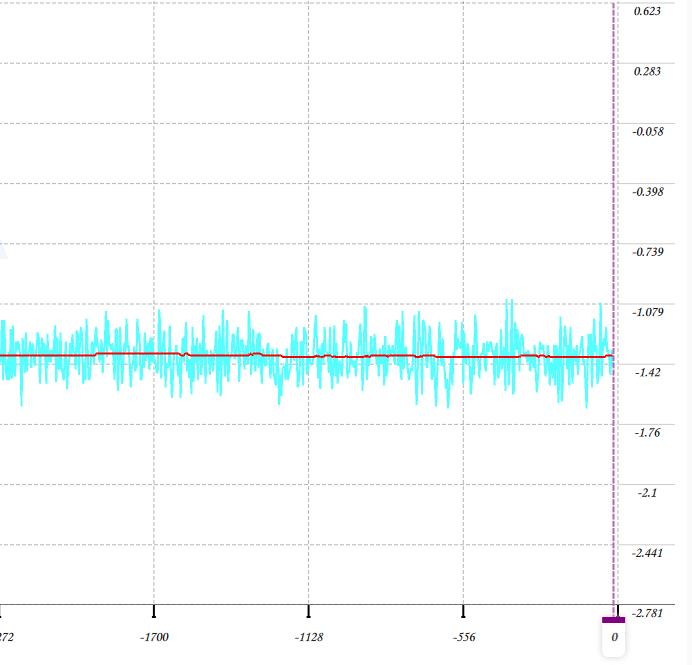
对比发现，加了卡尔曼滤波之后，数据更加平滑，贴近真实值。