62. 不同路径

Posted 2021-09-15 炫云云

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

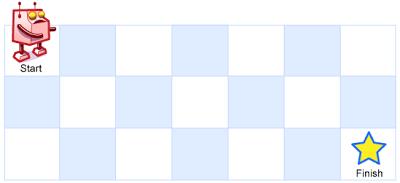
输入：m = 3, n = 7
输出：28

动态规划

我们用 $dp(i,j)$​ 表示从左上角走到 $(i,j)$​ 的路径数量，其中 $i$​ 和 $j$​ 的范围分别是 $[0,m)$​ 和 $[0,n)$​ 。

由于我们每一步只能从向下或者向右移动一步，因此要想走到 $(i,j)$, 如果向下走一步， 那么会从 $(i-1,j)$ 走过来; 如果向右走一步，那么会从 $(i,j-1)$​ 走过来。因此我们可以写出动态规划转移方程：
$$dp(i,j)=dp(i-1,j)+dp(i,j-1)$$
需要注意的是，如果 $i=0$, 那么 $dp(i-1,j)$ 并不是一个满足要求的状态，我们需要忽略这一项; 同理，如果 $j=0$, 那么 $dp(i,j-1)$​​ 并不是一个满足要求的状态，我们需要忽略这一项。

$dp(0,j)$ 和 $dp(i,0)$ 为边界条件，它们的值均为 11。

初始条件为 $f(0,0)=1$ ， 即从左上角走到左上角有一种方法。
最终的答案即为 $dp(m-1,n-1)$ 。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[1]*n] + [[1] + [0]*(n-1) for _ in range(m-1)]
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j] +dp[i][j-1]
        return dp[m-1][n-1]

组合数学

从左上角到右下角的过程中，我们需要移动 $m+n-2$ 次，其中有 $m-1$ 次向下移动， $n-1$ 次向 右移动。因此路径的总数，就等于从 $m+n-2$ 次移动中选择 $m-1$ 次向下移动的方案数，即组合数：
$$C_{m+n-2}^{m-1}=\left(\begin{array}{c}m+n-2\\ m-1\end{array}\right)=\frac{(m+n-2)(m+n-3)\cdots n}{(m-1)!}=\frac{(m+n-2)!}{(m-1)!(n-1)!}$$
因此我们直接计算出这个组合数即可。计算的方法有很多种：

• 如果使用的语言有组合数计算的 $\mathrm{A}\mathrm{P}\mathrm{I}$, 我们可以调用 API 计算;
• 如果没有相应的 $\mathrm{A}\mathrm{P}\mathrm{I}$, 我们可以使用 $\frac{(m+n-2)(m+n-3)\cdots n}{(m-1)!}$​ 进行计算。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        return comb(m+n-2 , n-1)

def uniquePaths(self, m: int, n: int) -> int:
        return int(math.factorial(m+n-2)/math.factorial(m-1)/math.factorial(n-1))

递归

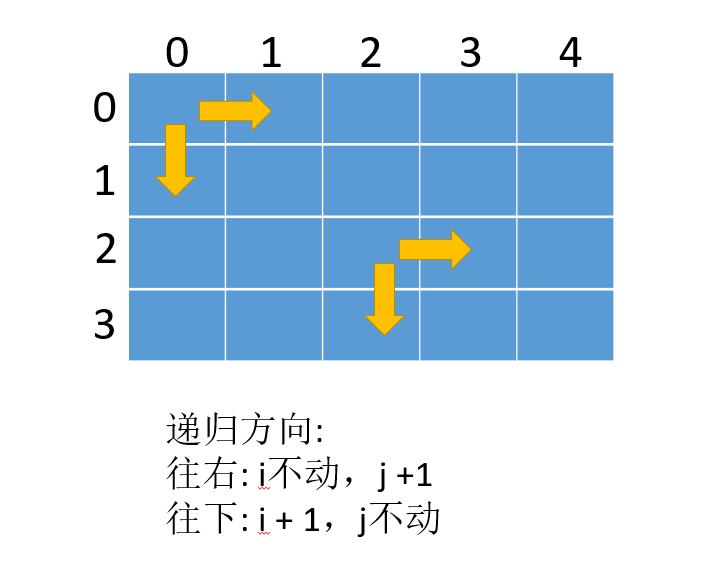
那么从(0,0)出发，走到(m,n)的所有路径，应该是由两条路线加起来的：

1. 从(0,0)为起点，往右的所有路径
2. 从(0,0)为起点，往下的所有路径

所以递归的核心逻辑就是:

$result=dfs(i+1,j)+dfs(i,j+1)$

当i == m - 1时，或者j == n - 1时，递归返回。

class Solution(object):
    def uniquePaths(self, m, n):
        d = {}
        def dfs(i, j):
            # 如果(i,j)在缓存中则直接返回
            if (i,j) in d:
                return d[i,j]
            # 到达边界时，返回 1  
            if i == m-1 or j == n-1:
                return 1
            else: # 继续递归调用，往下i+1，往右j+1   
                d[i,j] = dfs(i+1,j) +dfs(i,j+1)
            return d[i,j]
        return dfs(0,0)

滚动数组

我们在二维数组推导的时发现，dp[i][j]的值来自于dp[i - 1][j]和dp[i][j - 1]。

也就是只需要上一行的值就可以了，上上一行的并不需要了，所以这里可以用滚动数组的方式优化一下空间。

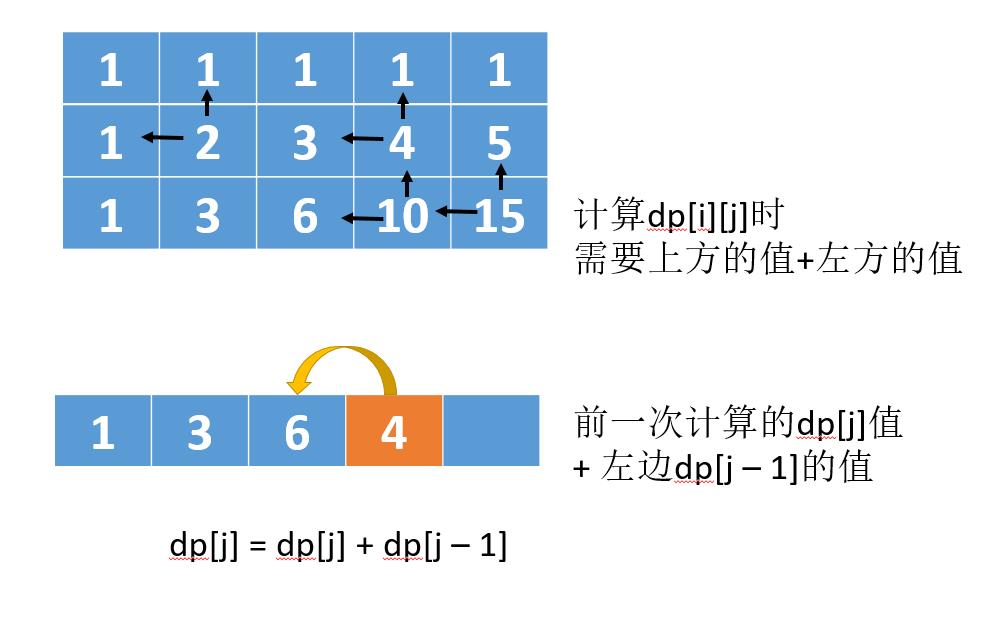
以上图所述，对于第三行10这个值，需要上方的值+左方的值。而经过上一次计算之后，第四列的值是4。

此时我们并不需要再跟上一行的做累加，只需要用4加上左边的6就可以了。

将原先
$$dp[i][j]=dp[i-1][j]+dp[i][j-1]$$
改为：
$$dp[j]=dp[j]+dp[j-1]$$
即上一行的+左边的值。

class Solution(object):
    def uniquePaths(self, m, n):
        # 一维空间，其大小为 n
        dp = [1] * n
        for i in range(1, m):
            for j in range(1, n):
                # 等式右边的 dp[j]是上一次计算后的，加上左边的dp[j-1]即为当前结果
                dp[j] = dp[j] + dp[j - 1]
        return dp[-1]

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)