回溯算法 python

Posted 2021-09-15 炫云云

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了回溯算法 python相关的知识，希望对你有一定的参考价值。

文章目录

前言

回溯算法其实就是我们常说的 DFS 算法，本质上就是一种暴力穷举算法。

回溯法

采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

找到一个可能存在的正确的答案；
在尝试了所有可能的分步方法后宣告该问题没有答案。

深度优先搜索 （英语：Depth-First-Search，DFS）

一种用于遍历或搜索树或图的算法。这个算法会 尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过，搜索将回溯到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点，则选择其中一个作为源结点并重复以上过程，整个进程反复进行直到所有结点都被访问为止。

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

路径：也就是已经做出的选择。
选择列表：也就是你当前可以做的选择。
结束条件：也就是到达决策树底层，无法再做选择的条件。

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

全排列

给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

那么我们当时是怎么穷举全排列的呢？比方说给三个数 [1,2,3]，你肯定不会无规律地乱穷举，一般是这样：
先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……

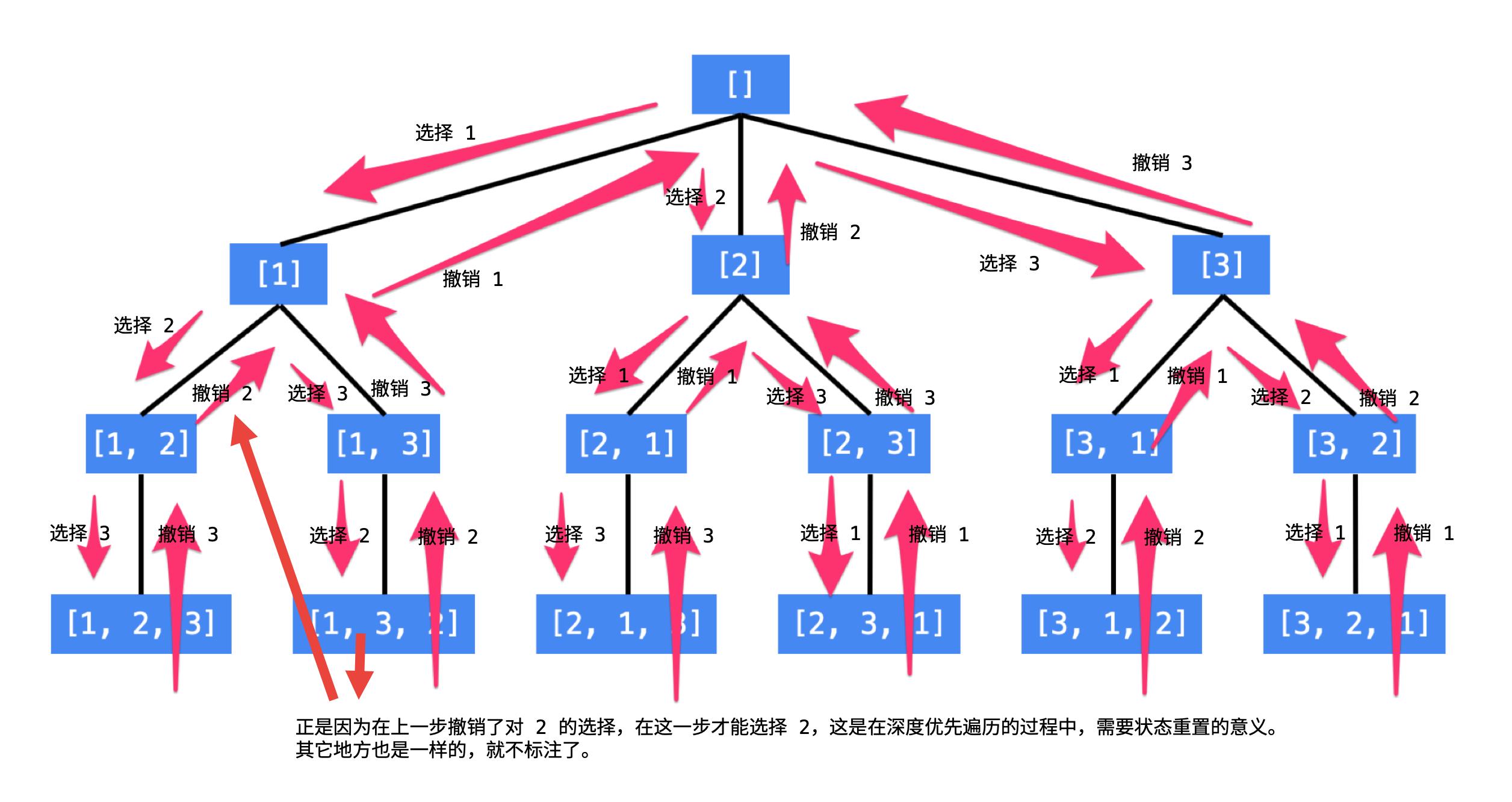
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。

我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其「路径」就是一个全排列。

再进一步，如何遍历一棵树？各种搜索问题其实都是树的遍历问题，而多叉树的遍历框架就是这样：

def traverse(root):
        // 前序遍历需要的操作
        traverse(child);
        // 后序遍历需要的操作

而所谓的前序遍历和后序遍历，他们只是两个很有用的时间点，我给你画张图你就明白了：

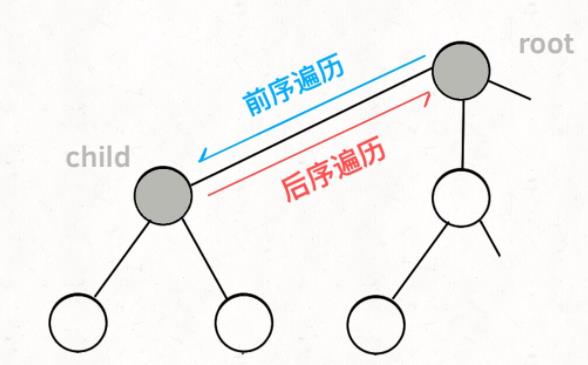
前序遍历的代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行。

回想我们刚才说的，「路径」和「选择」是每个节点的属性，函数在树上游走要正确维护节点的属性，那么就要在这两个特殊时间点搞点动作：

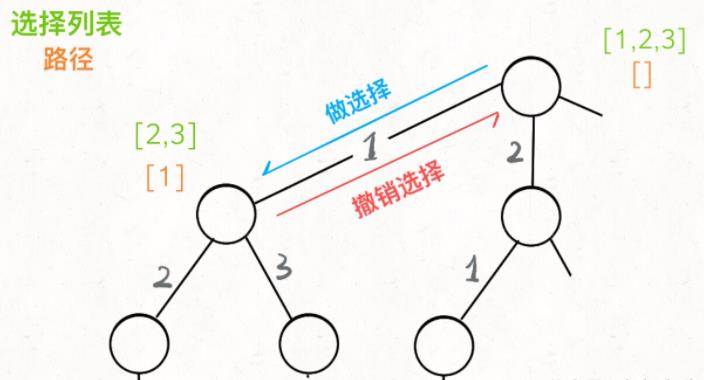
现在，你是否理解了回溯算法的这段核心框架？

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []
        n = len(nums)
        def backtrack(index = 0):
            if index == n:# 所有数都填完了
                res.append(path[:])
                return
            for i in range(0, n):
                intinuef nums[i] in path:
                    co
                path.append(nums[i])
                backtrack(index+1)
                path.pop()
   
        backtrack(0)
        return res

N 皇后

第四：搜索算法应用 - 四皇后问题

第三：启发式搜索：A* 算法

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

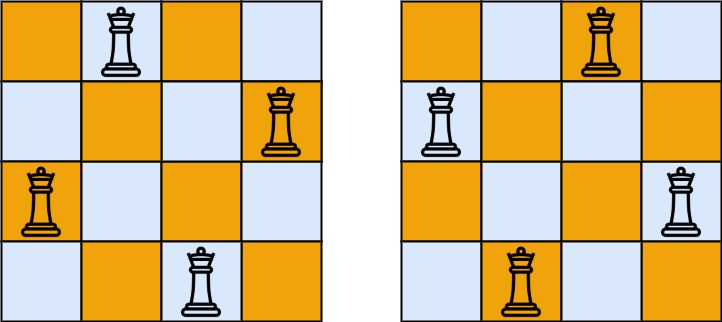
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

小技巧：记住已经摆放的皇后的位置

放置的规则是：由于一行内不能放置两个皇后，所以我们按行尝试，一行一行考虑皇后可以放置在哪一个位置上，某一行在考虑某一列是否可以放置皇后的时候，需要根据前面已经放置的皇后的位置。

由于是一行一行考虑放置皇后，摆放的这些皇后肯定不在同一行，为了避免它们在同一列，需要一个长度为 $N$ 的布尔数组 cols，已经放置的皇后占据的列，就需要在对应的列的位置标注为 True。

先尝试画出递归树，以 4 皇后问题为例，画出的递归树如下：

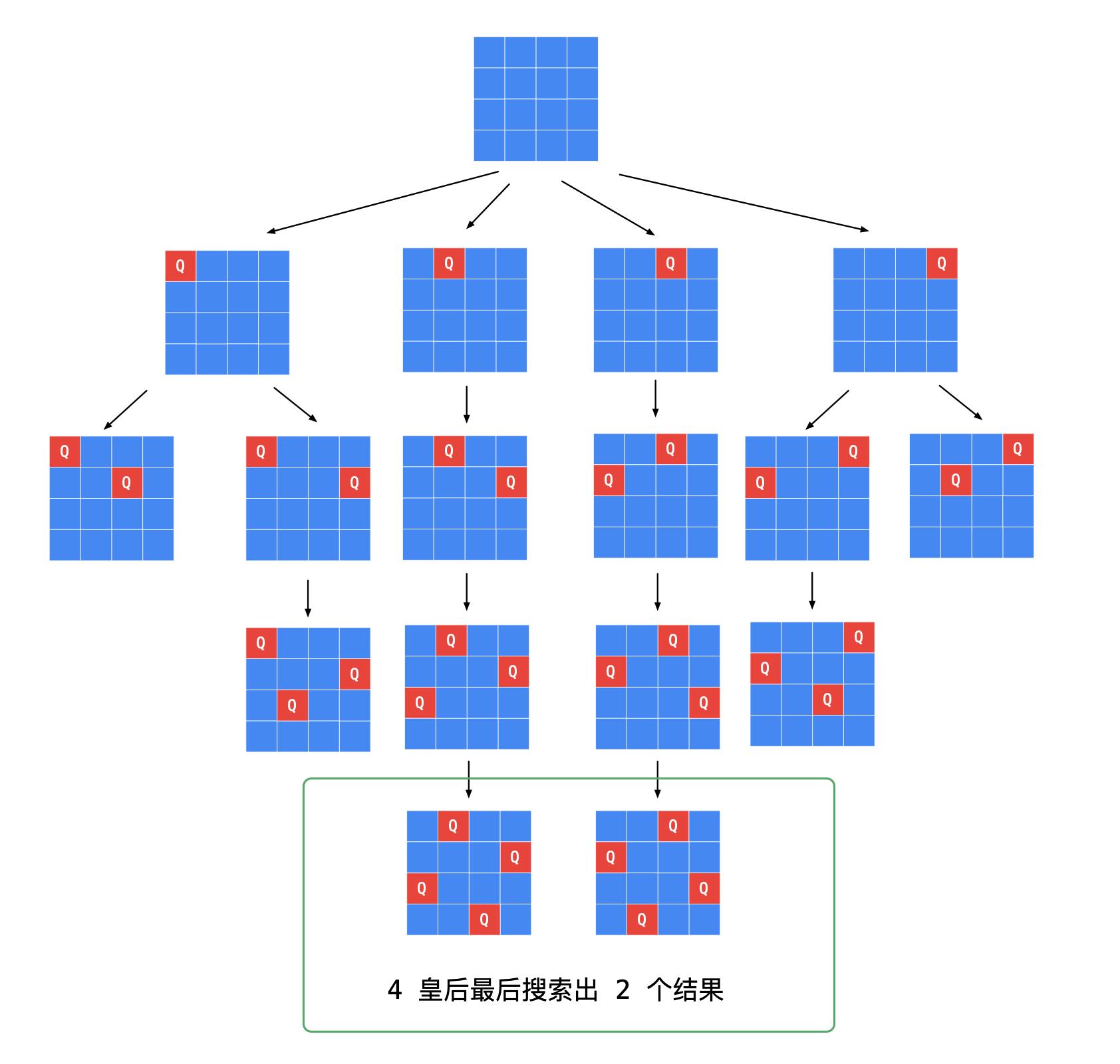
搜索的过程蕴含了剪枝的思想。「剪枝」的依据是：题目中给出的「N 皇后」的摆放规则：1、不在同一行；2、不在同一列；3、不在同一主对角线方向上；4、不在同一副对角线方向上。

首先我们模拟棋盘格子，生成一个 n * n格子的棋盘，每个格子的值都是"."。我们用row表示行，然后检查行中的每一列col，判断[row,col]这个位置是否可以放置皇后，如果能放置皇后，就将棋盘格[row,col]的位置设置为Q，然后继续尝试下一行。直到 $r o w = = n$ ，此时所有的皇后都放置完了，那么这时的棋盘就是一个完整的解法，我们直接将此棋盘格子的快照保存下来即可。

伪代码如下：

dfs(row, path)
    if row==n :
        //如果x等于n了，说明每行的皇后都放置完毕
        //将棋盘内容path的快照保存下来
        return

    for col in range(n):
        if [row,col]这个位置是有效的，即横、竖、两个斜线都有没有被攻击 
            将棋盘[row,col]位置设置为 Q
            dfs(row+1) 继续尝试下一行
            将棋盘[row,col]位置还原

考虑对角线（找规律）

下面我们研究一下主对角线或者副对角线上的元素有什么特性。在每一个单元格里写下行和列的下标。

每条副对角线 row + col 都有固定值。

为了保证至少两个皇后不同时出现在 同一主对角线方向 或者 同一副对角线方向。为「主对角线（Main diagonal）」和「副对角线（Sub diagonal）」设置相应的 布尔数组变量，只要排定一个「皇后」的位置，就需要占住对应的位置: sub[row + col] = True ,main[row - col + n - 1] = True，表示这条对角线已经有 $Q$ 。

查策略是，只要「检测」到新摆放的「皇后」与已经摆放好的「皇后」冲突 ,即在同一主对角线方向 或者 同一副对角线方向，就尝试摆放同一行的下一个位置，到行尾还不能放置皇后，就退回到上一行。

编码

我们使用一个 1 到 4 的排列表示一个 $\\times 4$ 的棋盘，例如：

得到一个符合要求的全排列以后，生成棋盘的代码就很简单了。

class Solution(object):
    def solveNQueens(self, n): 
        """ 
        n: int 
        rtype: List[List[str]] 
        """ 
        self.n =n 
        self.col = [False] * n  # 记录某一列是否放置了皇后          
        self.sub = [False] * (2 * n - 1) # 记录副对角线的单元格是否有皇后 
        self.main = [False] * (2 * n - 1) # 主对角线 
        self.res = []

        path = []
        self.dfs(0, path)
        return self.res

    def convert2board(self,path):
        board = []
        for num in path:
            row = list('.' * max(0,self.n))
            row[num] = 'Q'
            board.append("".join(row))
        return board

    def dfs(self,row, path):
        if row == self.n:
            '''
            深度优先遍历到下标为
            n，表示[0..n - 1]
            已经填完，得到了一个结果
            '''
            board = self.convert2board(path)
            self.res.append(board)

        # 针对下标为 row 的每一列，尝试是否可以放置
        for col in range(self.n):
            if not self.col[col] and not self.sub[row + col] and not self.main[row - col + self.n - 1]:
                path.append(col)
                self.col[col] = True
                self.sub[row + col] = True   #副对角线，横纵坐标之和不变
                self.main[row - col + self.n - 1] = True #主对角线，横-纵不变，+n-1移动到正区间

                self.dfs(row + 1, path)

                self.main[row - col + self.n - 1] = False
                self.sub[row + col] = False
                self.col[col] = False
                path.pop()