4.寻找两个正序数组的中位数
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了4.寻找两个正序数组的中位数相关的知识,希望对你有一定的参考价值。
4.寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
二分查找
直接求中位数可能不好想到,那么我们换个思路.假设有下面两个数组 A 和 B,A数组的长度是4,B数组的长度是8
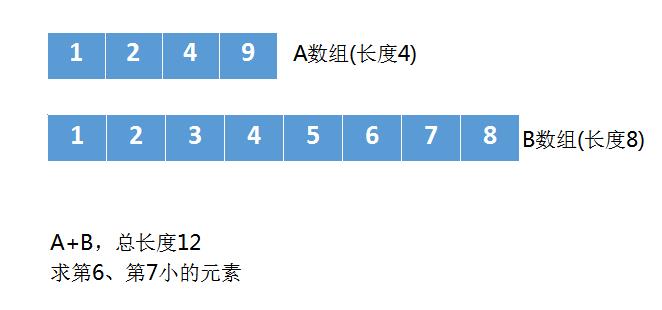
如上图,因为A+B的总长度是12,是偶数,所以求中位数的话,需要找到第6小、第7小的元素,找到这两个元素后,相加再 / 2 就可以了。
这里是偶数长度的情况,如果是两个数组长度相加后是奇数也是类似的,比如总长度是 13 ,那就需要找第7小的元素。
所以,这题可以转化为,如何找到第k小的元素。
- 如果总长度N是偶数,则需要找到两个数组中第
N / 2小的元素、第N / 2 + 1小的元素 - 如果总长度N是奇数,则需要找到两个数组中第
N / 2 + 1小的元素
题目限制了时间复杂度,所以这里找第k小的过程,肯定也是二分的方式。
因为数组A、数组B都是有序的,所以我们需要利用这个有用的特性, 二分查找缩小范围:第一次找 k 小、第二次就是找 k/2 小、然后是 k/4小,直到 k 等于1时。
还是以上面的数组为例,A数组为[1,2,4,9],B数组是[1,2,3,4,5,6,7,8]. 我们需要找第6、第7小的元素,假设我们先找第6小的元素,也就是k = 6。要找到第
k
k
k 个元素,我们可以比较
A
[
k
/
2
−
1
]
\\text{A}[k/2-1]
A[k/2−1]和
B
[
k
/
2
−
1
]
\\text{B}[k/2-1]
B[k/2−1]
我们首先比较 A数组中第3个元素,B数组中第3个元素,也就是A[k/2-1]和B[k/2-1],如下图:
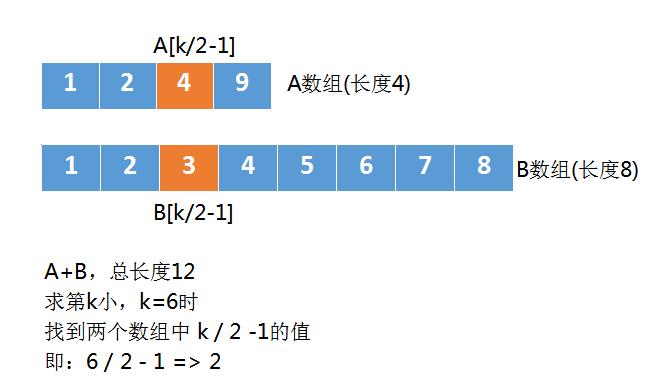
由于A[k/2-1] > B[k/2-1],这时候我们就可以忽略掉一些元素了。
上图中 A数组中的4,它前面有2个元素,也就是k/2-1个元素,B数组的3,它前面也有2个元素,也就是k/2-1个元素,所以橙色的4和3前面一共有k-2个元素
假设 B数组的3,也就是
B
[
k
/
2
−
1
]
B[k/2-1]
B[k/2−1] 比这k-2个元素都大。
而 B [ k / 2 − 1 ] B[k/2-1] B[k/2−1] 是小于 A [ k / 2 − 1 ] A[k/2-1] A[k/2−1]的,那么 B [ k / 2 − 1 ] B[k/2-1] B[k/2−1]相当于是第k-1小的,所以,第 k k k小的元素肯定不是它。这样的话,我们就可以排除一些元素了,刚才我们只是假设 B [ k / 2 − 1 ] B[k/2-1] B[k/2−1] 比 A [ k / 2 − 1 ] A[k/2-1] A[k/2−1]前面的元素大,实际可能不是.
但有一点可以肯定,既然 B [ k / 2 − 1 ] B[k/2-1] B[k/2−1]都不是第k小的元素,那么 B [ k / 2 − 1 ] B[k/2-1] B[k/2−1]前面的那些更不是了,于是我们将B[0]、B[1]、B[2]。。。B[k/2-1]这些元素全部忽略掉。
当我们忽略掉 B数组中的元素后, k也要跟着减小,原来我们求第6小,现在就是求第3小。这个解法的整体求解过程,就是不断缩小数组的规模,同时把k也跟着缩小。如下图
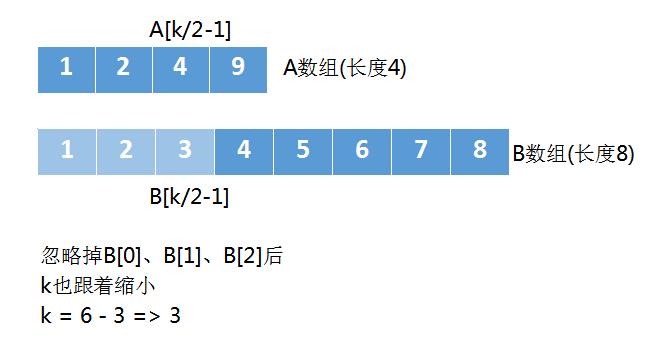
这次 k = 3 , k / 2 − 1 = 0 k=3,k/2-1=0 k=3,k/2−1=0,所以 A [ k / 2 − 1 ] A[k/2-1] A[k/2−1]对应的就是 A [ 0 ] , B [ k / 2 − 1 ] A[0],B[k/2-1] A[0],B[k/2−1]对应是 B [ 3 ] B[3] B[3],因为我们之前忽略掉了 B B B数组中的前3个元素,所以B数组的第1个元素是从下标3开始的。 如下图:
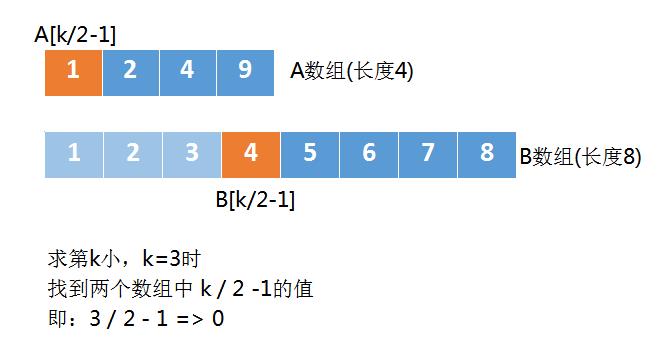
经过这次比较后, A [ k / 2 − 1 ] < B [ k / 2 − 1 ] A[k/2-1] < B[k/2-1] A[k/2−1]<B[k/2−1],所以忽略掉 A [ 0 ] A[0] A[0],然后将 k k k 变成2。
k k k此时等于2, k / 2 − 1 = 0 k/2-1= 0 k/2−1=0,于是 A [ k / 2 − 1 ] A[k/2-1] A[k/2−1]对应的是 A [ 1 ] A[1] A[1],因为刚才已经忽略掉A[0]了,B[k/2-1]对应的是B[3],如下图:
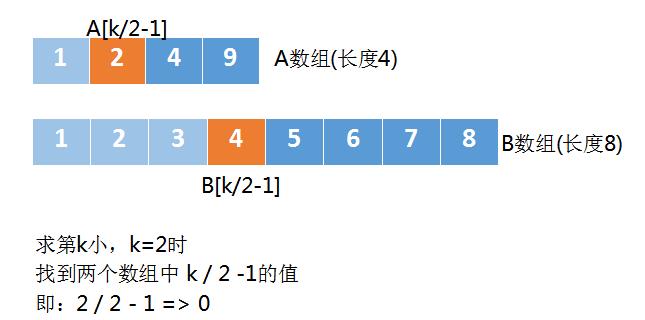
当 k = = 1 k==1 k==1时,返回A数组中第一个元素 和 B数组中第一个元素的较小者。
此时A数组中的第1个元素是 A [ 2 ] A[2] A[2],B数组中第1个元素是 B [ 3 ] B[3] B[3],即求 m i n ( A [ 2 ] , B [ 3 ] ) min(A[2],B[3]) min(A[2],B[3])
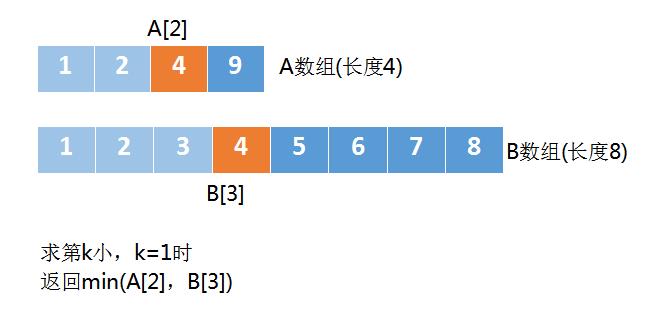
总结一下,对于求第k小的元素,其过程如下:
- 如果A[k/2-1] <= B[k/2-1],将A[0] - A[k/2-1]这些元素全部忽略掉
- 否则,将B[0] - B[k/2-1] 这些元素全部忽略掉
有以下三种情况需要特殊处理:
- 如果 A [ k / 2 − 1 ] \\text{A}[k/2-1] A[k/2−1] 或者 B [ k / 2 − 1 ] \\text{B}[k/2-1] B[k/2−1] 越界,那么我们可以选取对应数组中的最后一个元素。在这种情况下,我们必须根据排除数的个数减少 k k k 的值,而不能直接将 k k k 减去 k / 2 k/2 k/2 。
- 如果一个数组为空,说明该数组中的所有元素都被排除,我们可以直接返回另一个数组中第 k k k 小的元素。
- 如果 k = 1 k=1 k=1 ,我们只要返回两个数组首元素的最小值即可。
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
"""主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k//2-1] 和 pivot2 = nums2[k//2-1] 进行比较
- 这里的 "//" 表示整除
nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
"""
total = len(nums1) + len(nums2)
# 如果A数组长度+B数组长度total是奇数,则找total/2+1小的元素
# 即为中位数
if total % 2 == 1:
midIndex = total // 2 + 1
res = self.getKthElement(nums1, nums2, midIndex)
return float(res)
# 否则,找total/2,total/2+1这两个元素
else:
midIndex_1 = total // 2
midIndex_2 = total // 2 + 1
a = self.getKthElement(nums1, nums2, midIndex_1)
b = self.getKthElement(nums1, nums2, midIndex_2)
return (a + b) / 2.0
def getKthElement(self,nums1, nums2, k):
len1 = len(nums1)
len2 = len(nums2)
index1 = 0 # 直向忽略后的索引
index2 = 0
while True:
# 边界情况,当index1越界时,直接返回nums2的第k小元素
if index1 == len1:
return nums2[index2 + k -1]
# 边界情况,当index2越界时,直接返回nums1的第k小元素
if index2 == len2:
return nums1[index1 + k - 1]
# 边界情况,k等于1时,返回nums1第一个元素和nums2第一个元素较小者
if k == 1:
return min(nums1[index1], nums2[index2])
new_index1 = min(index1 + k // 2- 1 , len1- 1 )
new_index2 = min(index2 + k // 2 - 1, len2 - 1)
pivot1 = nums1[new_index1]
pivot2 = nums2[new_index2]
# 比较nums1[k/2-1]和nums2[k/2-1]
# 如果nums1的小,则忽略掉nums1[0] - nums1[k/2-1]这些元素
# 再更新 k,k 要减去忽略掉的那些元素,index1也要更新,待下轮使用
if pivot1 <= pivot2:
k -= (new_index1 - index1 + 1)
index1 = new_index1 + 1
# 如果nums2的小,则忽略掉nums2[0] - nums2[k/2-1]这些元素
# 再更新 k,k 要减去忽略掉的那些元素,index2也要更新,待下轮使用
else:
k -= (new_index2 - index2 + 1)
index2 = new_index2 + 1
参考
以上是关于4.寻找两个正序数组的中位数的主要内容,如果未能解决你的问题,请参考以下文章