LeetCode 342. 4的幂

Posted 2021-09-15 数据结构和算法

截止到目前我已经写了 600多道算法题，其中部分已经整理成了pdf文档，目前总共有1000多页（并且还会不断的增加），大家可以免费下载
下载链接：https://pan.baidu.com/s/1hjwK0ZeRxYGB8lIkbKuQgQ
提取码：6666

public boolean isPowerOfFour(int num) {
    //负数不可能是4的幂
    if (num <= 0)
        return false;
    //1是4的0次幂
    if (num == 1)
        return true;
    //如果不能够被4整除，肯定不是4的幂
    if (num % 4 != 0)
        return false;
    //如果能被4整除，除以4然后递归调用
    return isPowerOfFour(num / 4);
}

当然还可以一行代码搞定，但这种可读性不是太好

public boolean isPowerOfFour(int num) {
    return num > 0 && (num == 1 || (num % 4 == 0 && isPowerOfFour(num / 4)));
}

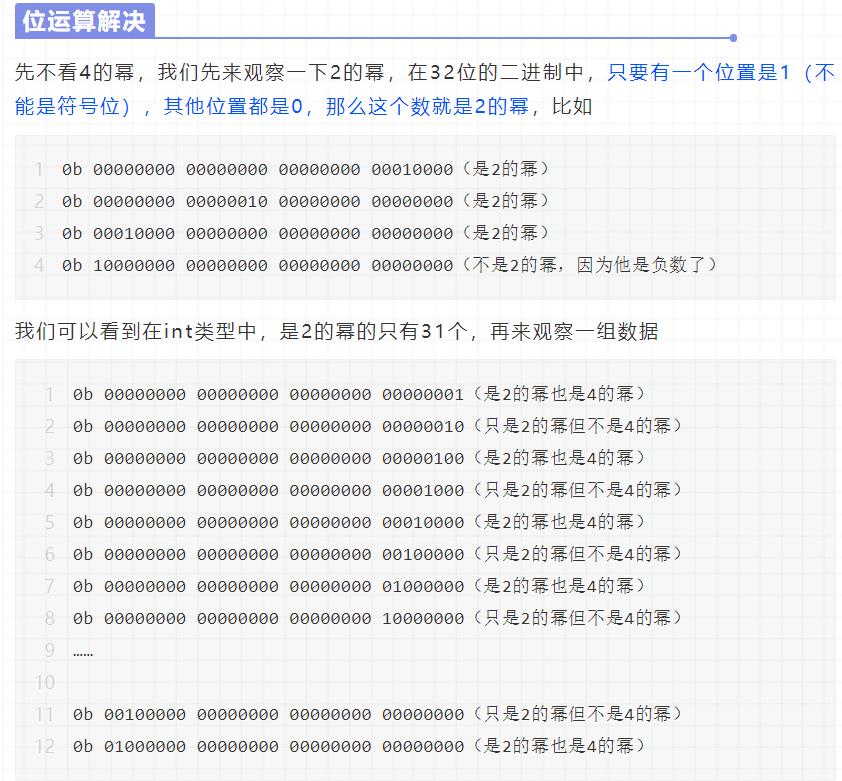
通过上面我们可以看到如果一个数是2的幂，并且二进制从右边数奇数位是1的一定是4的幂。判断是2的幂，我们只需要判断二进制中1的个数即可，这里可以参照425，剑指 Offer-二进制中1的个数，实际上还有一种更简单的方式，就是判断(num & (num - 1)) == 0，并且还要保证num>0；

最终代码如下

public boolean isPowerOfFour(int num) {
    return num > 0 && (num & (num - 1)) == 0 && (num & 0x55555555) == num;
}

注意这里0x55555555的二进制是

01010101 01010101 01010101 01010101

实际上还可以换一种方式

public boolean isPowerOfFour(int num) {
    return num > 0 && ((num & (num - 1)) == 0) && (num & 0xaaaaaaaa) == 0;
}

这里0xaaaaaaaa的二进制是

10101010 10101010 10101010 10101010

public boolean isPowerOfFour(int num) {
    return num > 0 && (num & (num - 1)) == 0 && (num - 1) % 3 == 0;
}

有没有一种可能就是一个数num是2的幂，但不是4的幂而且减去1还能被3整除呢，其实是没有这种可能的，如果一个数是2的幂但不是4的幂，那么这个数一定是2的奇次幂，类似于2^(2k+1)，我们来证明一下