最短路径算法——清晰简单的弗洛伊德算法(Floyd)

Posted 2021-09-15 土豆同学

弗洛伊德算法(Floyd)

\\qquad 上一篇文章介绍了迪杰斯特拉算法(Dijkstra)。具体请看：最短路径算法——简单明了的迪杰斯特拉算法(Dijkstra)。Dijkstra适用于非负权图，并且一次只能从网络中找源点到任何一个节点的最短路径，而Floyd算法的应用更加广泛，可以求网络中任意两点之间的最短路径，而且弗洛伊德算法适用于负权图，这篇文章就用图和表的形式来介绍一下弗洛伊德算法！

1 思想（原理）

\\qquad Floyd算法可以给出网络中任意两个节点之间的最短路径，因此它是比Dijkstra更一般的算法。Floyd算法的思想是将$n$个节点的网络表示为$n$行$n$列的矩阵，而矩阵中的元素$(i,j)$表示从节点$i$到节点$j$的距离$d_{ij}$，如果两点直接没有边相连，则相应的元素就是无穷$(\infty )$.

2 步骤

<1> 第0步：定义初始距离矩阵$D_0$、节点序列矩阵$S_0$，如下表。对角线上用”—“表示不需要从自身到自身。

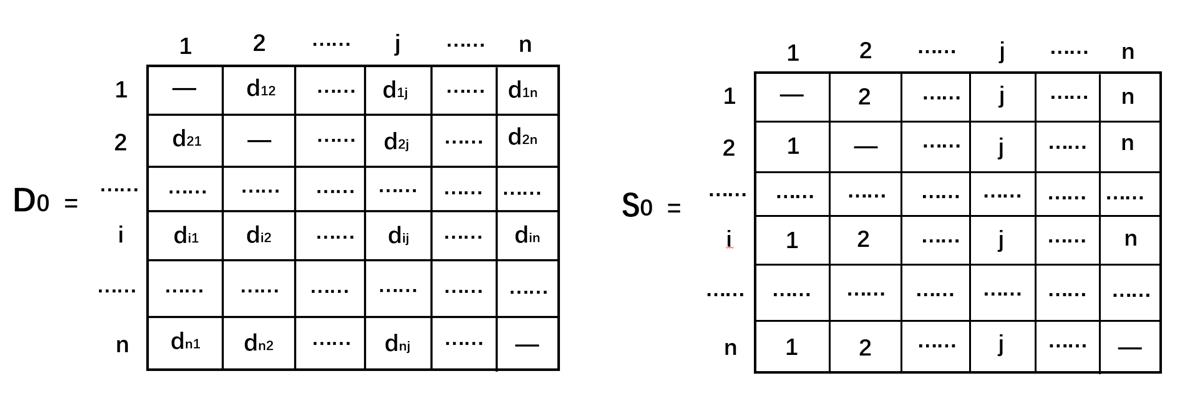
\\qquad 这里的节点序列矩阵相当于路线表，如下表，$S_{ij}=j$表示，从节点$i$到节点$j$只需经过节点$j$即可。

令$k=1$.

<2> 一般的第k步：令第$k$行为枢轴行，第$k$列为枢轴列。对于矩阵$D_{k-1}$（上一步完成后的矩阵）中对的每一个元素做三重操作。

如果满足条件：
$$d_{ik}+d_{kj}<d_{ij}(i\ne k,j\ne k,i\ne j)$$
则进行下面的操作：

<\\a> 用$d_{ik}+d_{kj}$代替矩阵$D_{k-1}$中的元素$d_{ij}$，从而得到矩阵$D_k$.
<\\b> 用$k$代替矩阵$S_{k-1}$中的元素$s_{ij}$，从而得到矩阵$S_k$.
<\\c> 令$k=k+1$，如果$k=n+1$，停止，否则重复<2>.

3 栗子

\\qquad 直接看方法步骤会感觉太抽象，这里用一个例子进行步骤的演示.
\\qquad 对下图中的网络，求任意两个节点之间的最短路径，图中弧上给出了相应节点间的距离。弧(3,5)是有向的，其他边都是双边。

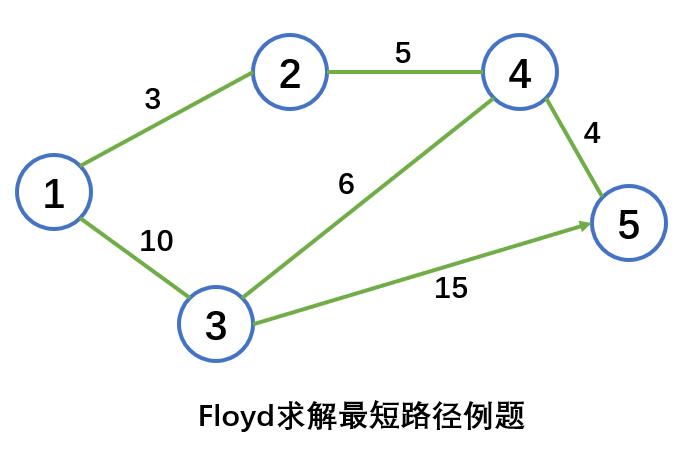
迭代0：矩阵$D_0$和$S_0$代表初始的网络。可以看到矩阵$D_0$除了$d_{53}=\infty$外(因为弧(3,5)是单向弧)，$D_0$是对称的。

迭代1：令$k=1$. $D_0$矩阵中的黄色阴影表示的第1行和第1列为枢轴行和枢轴列。根据三重操作发现可以改进的元素是$d_{23}$和$d_{32}$，即

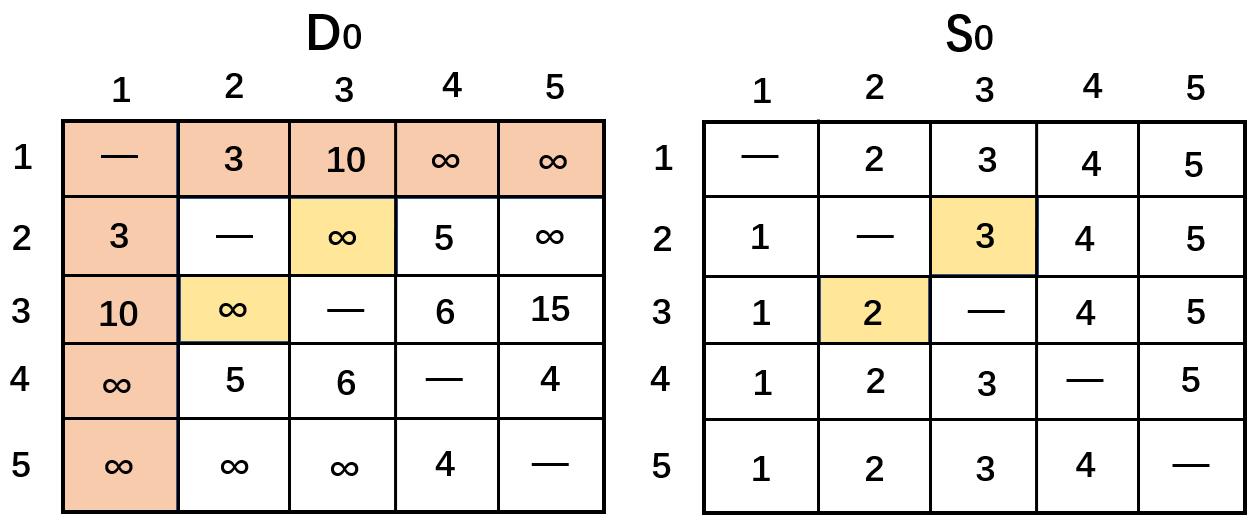
(1) $d_{21}+d_{13}=3+10<\infty$，则在$d_{23}$中用$13$代替$\infty$，并令$s_{23}=1$.
(2) $d_{31}+d_{12}=10+3<\infty$，则在$d_{32}$中用$13$代替$\infty$，并令$s_{32}=1$.

此时得到$D_1$和$S_1$，得到下表

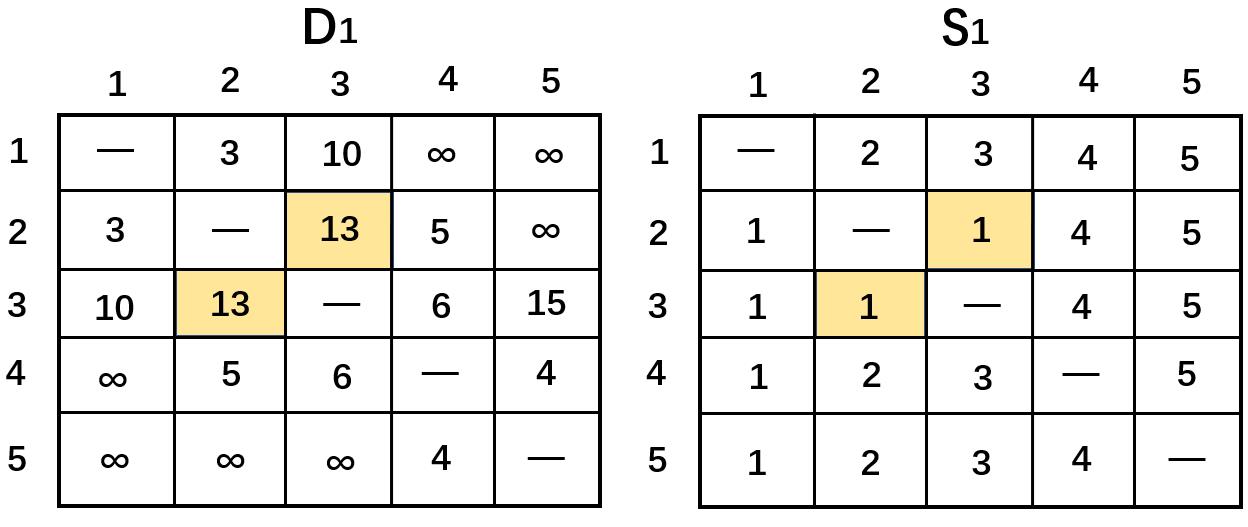
迭代2：令$k=2$. $D_0$矩阵中的黄色阴影表示的第2行和第2列为枢轴行和枢轴列。根据三重操作发现可以改进的元素是$d_{14}$和$d_{41}$，即

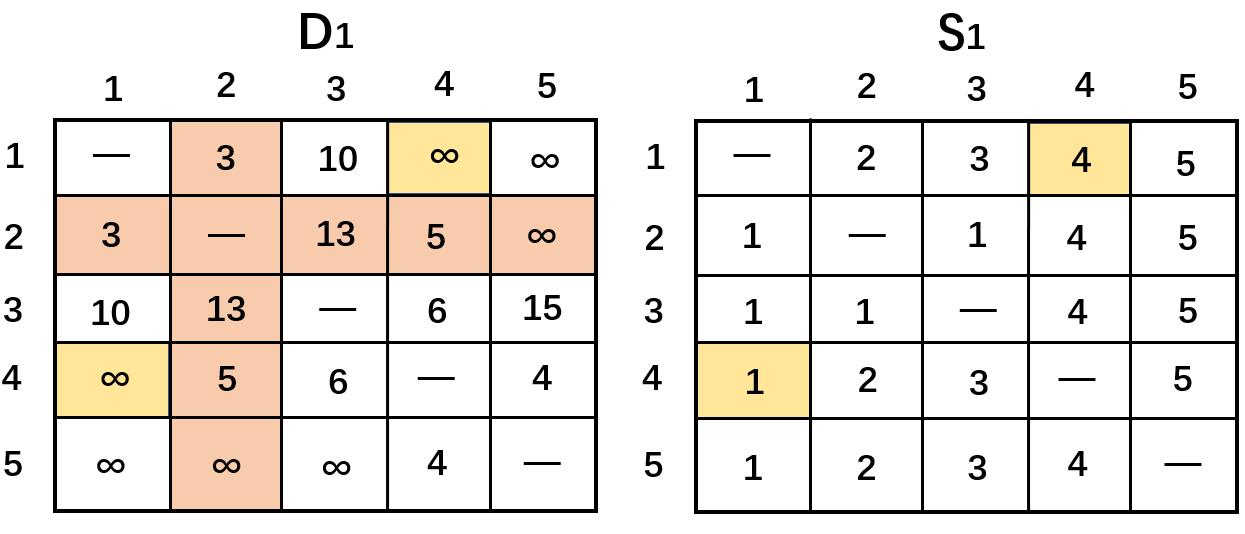
(1) $d_{21}+$

最短路径之Floyd算法

【数据结构】最短路径之迪杰斯特拉(Dijkstra)算法与弗洛伊德(Floyd)算法

算法弗洛伊德算法 最短路径算法

最短路径算法——弗洛伊德算法（Floyd）

[Python] 弗洛伊德(Floyd)算法求图的直径并记录路径

弗洛伊德（Floyd）算法求图的最短路径