一个简单有趣的小问题,枫叶嵌套问题的完美解决
Posted slandarer
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一个简单有趣的小问题,枫叶嵌套问题的完美解决相关的知识,希望对你有一定的参考价值。
前两天看到一个很有意思的小问题,描述如下:

思路也非常简单,我们首先检测枫叶中心,并用枫叶旋转来代替反方向的框旋转,获取旋转角
t
t
t 在
[
0
,
p
i
/
2
]
[0,pi/2]
[0,pi/2] 区间内,竖直高度变化和横向宽度变化,我们可以将这两个变化看作是连续的,因而我们只需要检测两个函数是否有交点即可,即是否:
∃
t
0
,
f
x
(
t
0
)
−
f
y
(
t
0
)
=
0
{\\exists}t_0,f_x(t_0)-f_y(t_0)=0
∃t0,fx(t0)−fy(t0)=0
由于我们很难获得这两个函数,实际上对于
f
x
(
t
)
−
f
y
(
t
)
f_x(t)-f_y(t)
fx(t)−fy(t),我们能得到的只有数组形式,因而我们只需要检测有没有相邻两个数相乘后数值<=0即可。
代码也不难实现,如下为含注释的完整代码:
function mapleInSquare
maplePic=imread('test3.png'); %读取图片
maplePic=rgb2gray(maplePic); %灰度化
boolPic=double(maplePic)<200; %确定枫叶区域
[RowSet,ColSet]=find(boolPic);%枫叶区域像素点坐标
%去中心化
RowCenter=(min(RowSet)+max(RowSet))/2;
ColCenter=(min(ColSet)+max(ColSet))/2;
RowSet=RowSet-RowCenter;
ColSet=ColSet-ColCenter;
pieceNum=200; %角度细化数目
thetaSet=linspace(0,pi/2,pieceNum);%将角度细化
%初始化
rowDiff=zeros(1,pieceNum);
colDiff=zeros(1,pieceNum);
for i=1:pieceNum
theta=thetaSet(i);
%像素点旋转
tempRowSet=cos(theta).*RowSet-sin(theta).*ColSet;
tempColSet=cos(theta).*ColSet+sin(theta).*RowSet;
%记录长度
rowDiff(i)=max(tempRowSet)-min(tempRowSet);
colDiff(i)=max(tempColSet)-min(tempColSet);
end
%图像显示:有交点说明有符合题意角度
figure(1)
hold on
plot(1:pieceNum,rowDiff,'LineWidth',1)
plot(1:pieceNum,colDiff,'LineWidth',1)
%做差后左右比较,检测f1(x)-f2(x)是否有零点,零点位置
diffData=rowDiff-colDiff;
multData=diffData(1:end-1).*diffData(2:end);
crossPos=find(multData<=0);
%如果存在交点
if ~isempty(crossPos)
%角度及边长矩阵
theta_edge_mat=zeros(length(crossPos),2);
for i=1:length(crossPos)
crossTheta=(thetaSet(crossPos(i))+thetaSet(crossPos(i)+1))/2;%旋转角度
theta_edge_mat(i,1)=crossTheta;
%像素点旋转
tempRowSet=cos(crossTheta).*RowSet-sin(crossTheta).*ColSet;
tempColSet=cos(crossTheta).*ColSet+sin(crossTheta).*RowSet;
%获取范围信息
rowRange=[min(tempRowSet),max(tempRowSet)];
colRange=[min(tempColSet),max(tempColSet)];
theta_edge_mat(i,2)=(rowRange(2)-rowRange(1)+colRange(2)-colRange(1))/2;
%获取旋转后的点集
pntSet=[rowRange(1),colRange(1);
rowRange(1),colRange(2);
rowRange(2),colRange(1);
rowRange(2),colRange(2)];
%旋转回去
newPntSet(:,1)=cos(-crossTheta).*pntSet(:,1)-sin(-crossTheta).*pntSet(:,2)+RowCenter;
newPntSet(:,2)=cos(-crossTheta).*pntSet(:,2)+sin(-crossTheta).*pntSet(:,1)+ColCenter;
%绘图
figure(i+1)
imshow(maplePic)
hold on
plot(newPntSet([1 2],2),newPntSet([1 2],1),'r','LineWidth',1)
plot(newPntSet([2 4],2),newPntSet([2 4],1),'r','LineWidth',1)
plot(newPntSet([1 3],2),newPntSet([1 3],1),'r','LineWidth',1)
plot(newPntSet([4 3],2),newPntSet([4 3],1),'r','LineWidth',1)
end
end
%结果输出
disp(theta_edge_mat)
end
由于我没有下载题目数据哈,于是自己找了几张图试了试,效果还不错:
示例一:

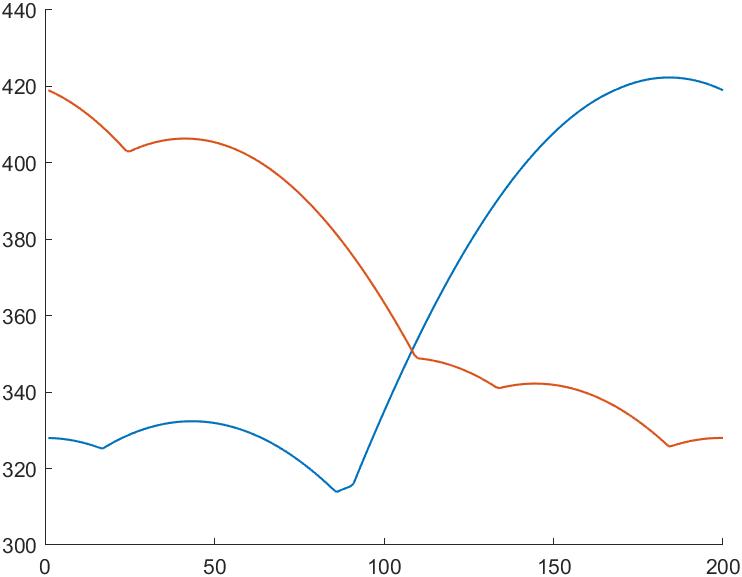

旋转角及边长
0.8485 350.8903
示例二:

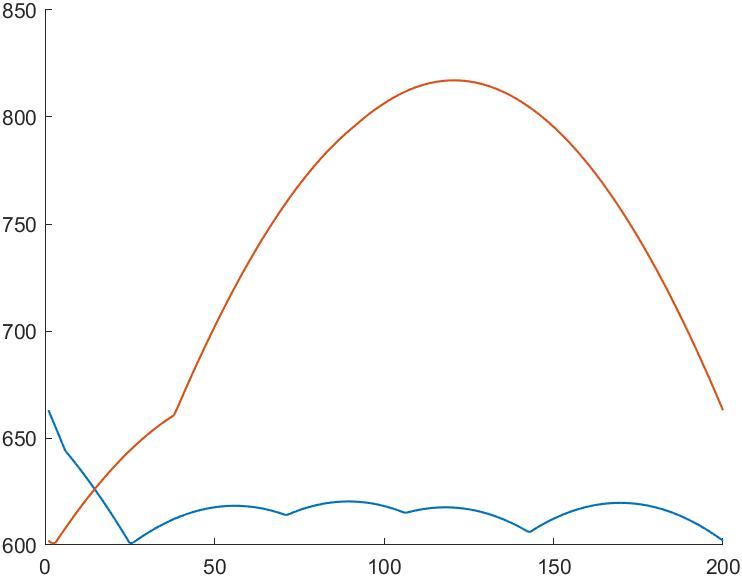

旋转角及边长
0.1066 626.1161
示例三(多个正方形符合情况):
实际上是将实例一叶柄截短了点,让他更方了:

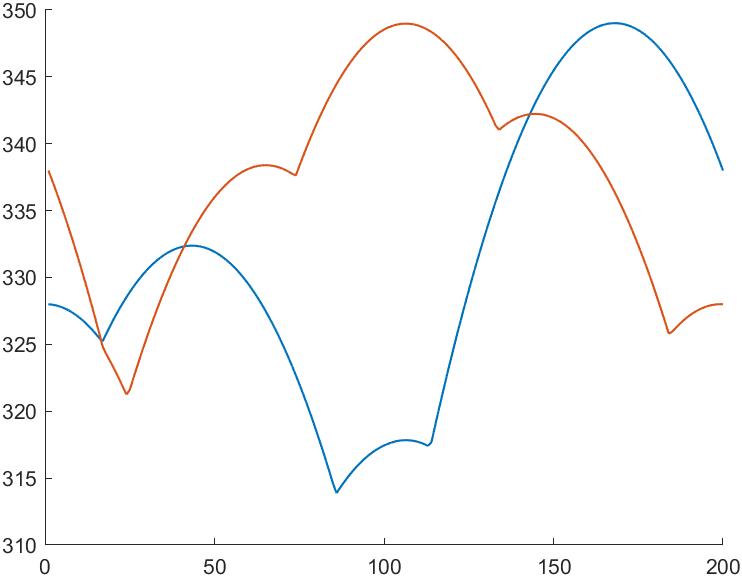

旋转角及边长
0.1223 325.3239
0.3197 332.4445
1.1248 342.3447
以上是关于一个简单有趣的小问题,枫叶嵌套问题的完美解决的主要内容,如果未能解决你的问题,请参考以下文章