容斥原理_集合相交问题

Posted 2021-09-13 一只特立独行的猫

问题引入：

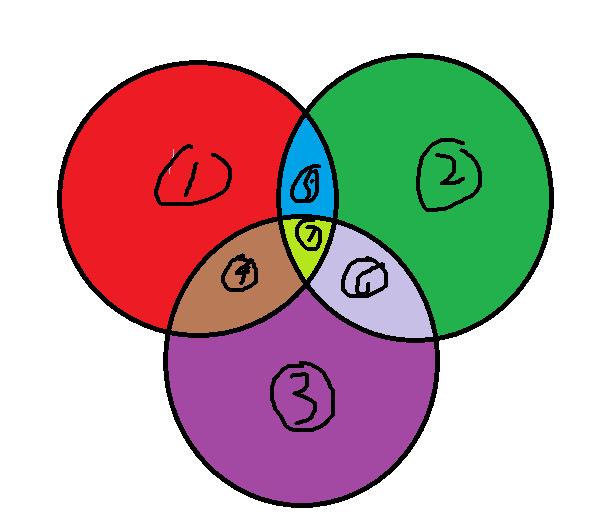
在求如上三个圆围成的面积时，通常是用

S(1∪2∪3) = S(1) + S(2) + S(3) - S(1∩2) - S(1∩3) - S(2∩3) + S(1∩2∩3)

的方法进行处理。就其原理就是先统计总的，再逐步进行减法。

推广

$S(1U2U...Un)=S(1)+S(2)+...+S(n)$
$-S(1\cap 2)-S(1\cap 3)-...-S(1\cap n)-S(2\cap 3)-...-S(n-1\cap n)$
$+S(1\cap 2\cap 3)+S(1\cap 2\cap 4)+...+S(n-2\cap n-1\cap n)$
$...$
观察上式，可以发现，就是总面积等于奇数个图形的∩的和和偶数个图形的∩的差。
可以归纳出如下式子：
f(x):由x个图形交集的面积
$S=f(1)-f(2)+...+(-1{)}^{k-1}f(k)$

例题：

代码：

其中，对n个数分别取1,2,3…个数通过累加二进制位来实现。

#include<iostream>

using namespace std;

typedef long long LL;

int p[20];

int main(){
    int n,m;
    LL sum=0;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        cin>>p[i];
    }
    for(int i=1;i<(1<<m);i++){
        LL cnt=0,t=1;//cnt判断奇偶性
        for(int j=0;j<m;j++){
            if((i>>j)&1){
                t*=p[j];
                cnt++;
            }
        }
        if(cnt&1){
            sum+=n/t;
        }else{
            sum-=n/t;
        }
    }
    cout<<sum<<endl;
    return 0;
}

原题链接