剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

Posted 2021-09-13 炫云云

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 $p、q$，最近公共祖先表示为一个结点 $x$，满足 $x$ 是 $p、q$ 的祖先且 $x$ 的深度尽可能大，即与$p、q$距离最近（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

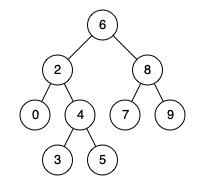
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6

解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2

解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

• 所有节点的值都是唯一的。
• p、q 为不同节点且均存在于给定的二叉搜索树中。

两次遍历

思路与算法

注意到题目中给出的是一棵「二叉搜索树」，因此我们可以快速地找出树中的某个节点以及从根节点到该节点的路径，例如我们需要找到节点 $p$：

我们从根节点开始遍历；

• 如果当前节点就是 p，那么成功地找到了节点；
• 如果当前节点的值大于 p 的值，说明 p 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；
• 如果当前节点的值小于 p 的值，说明 p 应该在当前节点的右子树，因此将当前节点移动到它的右子节点。

对于节点 q 同理。在寻找节点的过程中，我们可以顺便记录经过的节点，这样就得到了从根节点到被寻找节点的路径。

当我们分别得到了从根节点到 $p$​ 和 $q$​ 的路径之后，我们就可以很方便地找到它们的最近公共祖先了。显然，$p$​ 和 $q$​ 的最近公共祖先就是从根节点到它们路径上的「分岔点」，也就是最后一个相同的节点。因此，如果我们设从根节点到 $p$ 的路径为数组 $\text{path\_p}[]$​ ，从根节点到 $q$ 的路径为数组 $\text{path\_q}[]$​ ，那么只要找出最大的编号 $i$​​​​，其满足
$$\text{path\_p}[i]=\text{path\_q}[i]$$
那么对应的节点就是「分岔点」，即 $p$ 和 $q$ 的最近公共祖先就是 「分岔点」.

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        def getPath(root,target ):
            path = list()
            node = root
            while node !=target:
                path.append(node)
                if target.val<node.val:
                    node = node.left
                else:
                    node = node.right
            path.append(node) # target点
            return path
        path_p = getPath(root,p)
        path_q = getPath(root,q)
        for u ,v in zip(path_p,path_q):
            if u ==v:
                ancestor =u
            else:
                break
        return ancestor

一次遍历

根据二叉搜索树的特性，我们可以发现，这里其中有一定的规律：

• 如果 $p$ 和 $q$ 节点值均小于根节点值时，那么此时应该在根的左子树中找答案（如示例 2）；
• 如果 $p$ 和 $q$ 节点值均大于根节点值时，那么应该在根的右子树中找答案。

上面两种情况，$p$ 和 $q$ 节点值要么都小于根节点值，要么都大于根节点值。其他情况该如何处理？

这里先罗列下可能的三种情况：

• $p$ 和 $q$ 分布在根节点的左右子树中；（如示例 1）
• $p$ 是 $q$ 的父节点，且 $p$ 为根节点；
• $q$ 是 $p$ 的父节点，且 $q$​ 为根节点。

我们先说下这三者的结论，三者最终返回的都是根节点。

第一种情况可能比较好理解，这里 $p$ 和 $q$ 分布在根的左右子树，两者往上追溯祖先节点即是根节点。

第二种情况，这里先看下题目中的一个信息，如下：

• 一个节点也可以是它自己的祖先。
• 因为 p 是 q 的父节点，那么 p 可作为 q 的祖先，而 p 也可作为自身祖先。那么 p 就是 p 和 q 的最近公共祖先。此时 p 为根节点，那么返回的结果即是根节点。

第三种情况，与第二种情况同理。

这里，我们以示例 2 为例，以图示来理解下上面所述的分析：

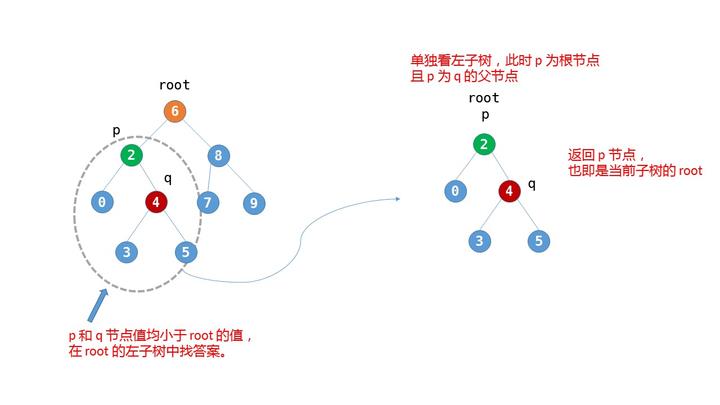
代码：

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        ancestor = root
        while True:
            if p.val<ancestor.val and q.val <ancestor.val:
                ancestor = ancestor.left:
            elif p.val > ancestor.val and q.val > ancestor.val:
                ancestor = ancestor.right
            else:
                break
        return ancestor

递归（dfs）

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        def DFS(root):
            nonlocal res, flag
            if not root or flag:
                return
            if q.val <root.val and p.val<root.val:
                DFS(root.left)
            elif q.val >root.val and p.val>root.val:
                DFS(root.right)
            else:
                res = root
                flag = True
        flag = False
        res = TreeNode()
        DFS(root)
        return res

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)