[多项式前缀和差分]智乃酱的静态数组维护问题多项式

Posted 2021-09-13 鱼竿钓鱼干

[多项式前缀和差分]智乃酱的静态数组维护问题多项式

题目

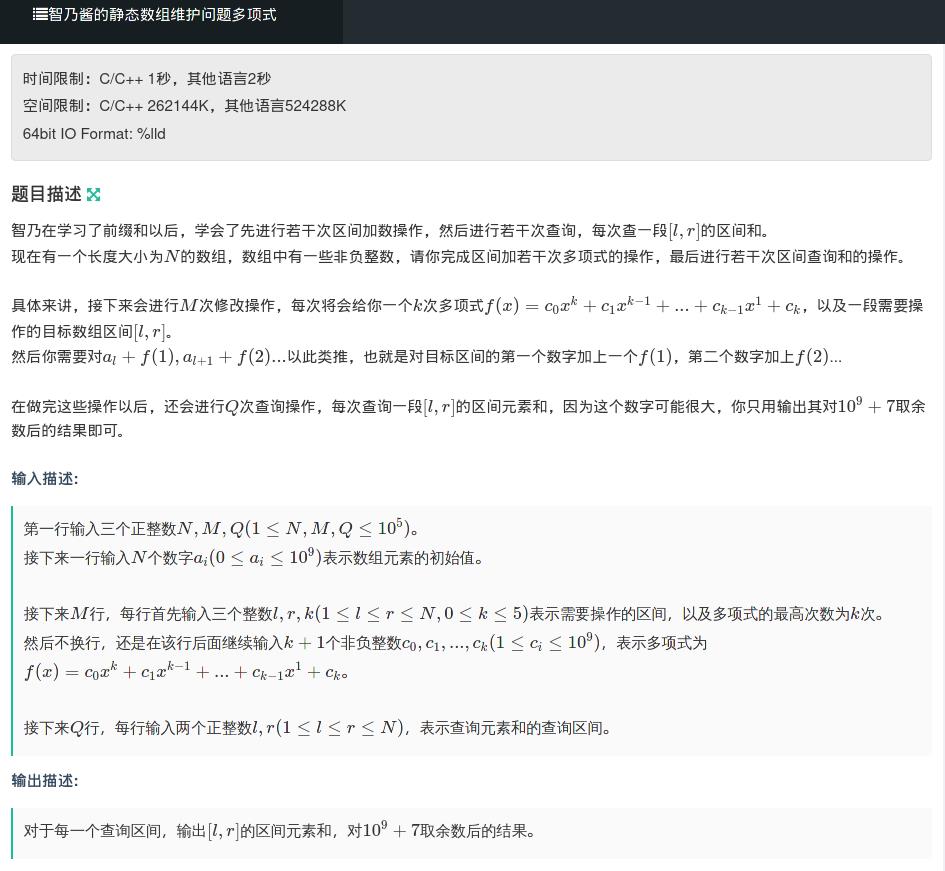
思路

参考资料
基本定理是：最高次为n次的多项式最多做n+1阶差分
最板的题目是，区间加一个常数，我们一般对a数组做一次差分然后在a[l]和a[r+1]做处理，然后前缀和还原。
对于多项式的差分前缀和。
我们首先对a数组做6次差分（k最多5次）。然后把多项式拆成单独的$x^i$的形式，做6次差分。
需要注意的事情是，每做一次差分，对应的位置都会偏移，因此每一阶差分不都是处理$D[l]$和$D[r+1]$。
对k阶差分后a数组加上k阶差分后的f多项式进行前缀和还原，效果等于在l,r处加上f多项式。同时我们可以构造多项式$-f(i+r-l+1)$来作为逆运算实现区间修改

这题数据小所以可以直接暴力
如果数据量大的花，要考虑卷积优化。

代码

参考前缀和练习

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pii pair<int,int>
#define pll pair<ll,ll>
#define pli pair<ll,int>
#define Min(a,b,c)  min(a,min(b,c))
#define Max(a,b,c)  max(a,max(b,c))

typedef long long ll;
typedef unsigned long long ull;

const double pi = 3.141592653589793;
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;

const int N = 100010;
const ll mod = 1000000007;

ll a[N], p[10], f1[10], f2[10];

void S(ll a[], int n, int t)
{
    while (t--)
    {
        for (int i = 1; i <= n; i++)
            a[i] = (a[i - 1] + a[i]) % mod;
    }
}

void D(ll a[], int n, int t)
{
    while (t--)
    {
        for (int i = n; i >= 1; i--)
            a[i] = (a[i] - a[i - 1]) % mod;
    }
}

ll f(ll x, ll p[], int k)//计算函数
{
    ll base = 1, ans = 0;
    for (int i = 0; i <= k; i++)
    {
        ans = (ans + p[i] * base % mod) % mod;
        base = base * x % mod;
    }
    return ans;
}

int main()
{
    int n, m, q;
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    D(a, n, 6);//根据定理，n次多项式最多做n+1次差分
    while (m--)
    {
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        for (int i = k; i >= 0; i--) scanf("%lld", &p[i]);
        for (int i = 1; i <= 6; i++) 
        {
            f1[i] = f(i, p, k);
            f2[i] = (mod - f(i + r - l + 1, p, k)) % mod;//构造逆运算
        } 
        D(f1, 6, 6);
        D(f2, 6, 6);
        for (int i = 1; i <= 6; i++)
        {
            a[l + i - 1] = (a[l + i - 1] + f1[i]) % mod;
            a[r + i] = (a[r + i] + f2[i]) % mod;
        }
    }
    S(a, n, 7);//求和
    while (q--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\\n", ((a[r] - a[l - 1]) % mod + mod) % mod);
    }
    return 0;
}