前缀和思想
Posted 吃花椒的妙酱
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了前缀和思想相关的知识,希望对你有一定的参考价值。
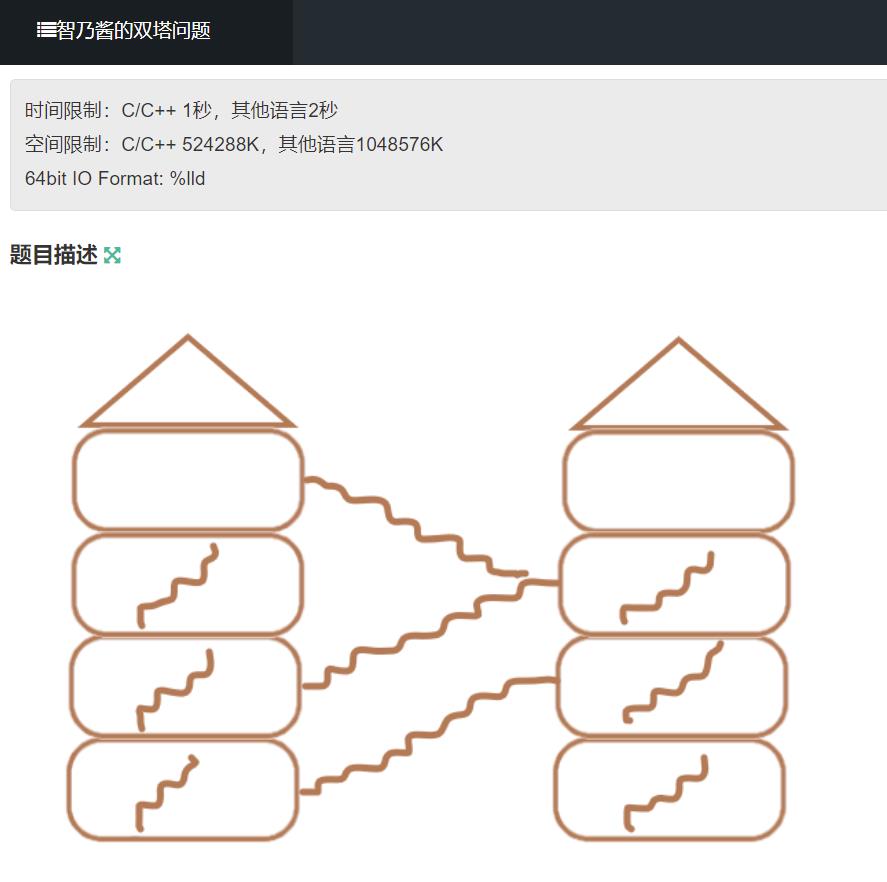

思路:dp,矩阵前缀和
容易想到转移方程
dp[i][0] = dp[i-1][0] + dp[i-1][1](若右到左有梯子)
dp[i][1] = dp[i-1][1] + dp[i-1][0](若左到右有梯子)
继续写下,以上dp式可以写成矩阵
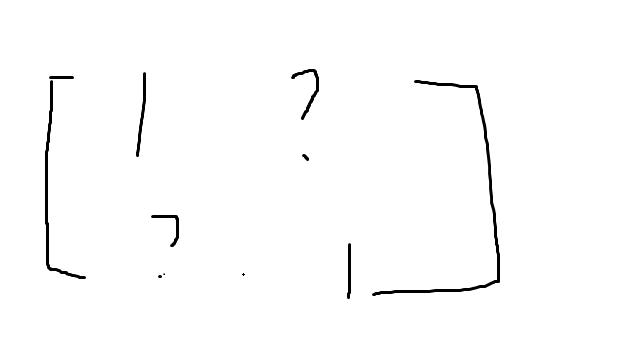
问号处就是梯子的情况
利用前缀积处理区间询问即可,有询问区间[l,r],普通前缀乘我们要做的就是r/l,因为矩阵左乘的性质,矩阵前缀积的处理则要转化为l的逆矩阵乘矩阵r,注意一下逆矩阵负数取模
现在我们改下题面,改成带修梯子方向的在线询问,怎么做?
一个思路是线段树维护区间矩阵积……
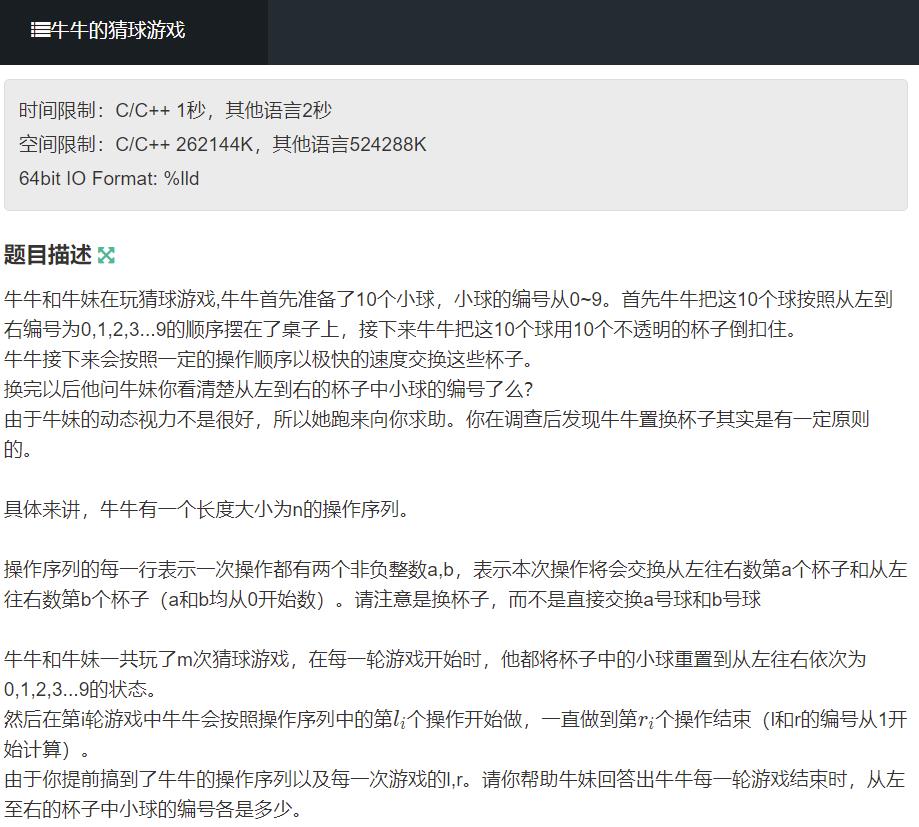

思路,容易想到球的交换有前缀和性质,就是不好写
假设我们现在有球1,2,3,交换得3,2,1
我们给3,2,1重新编号为1,2,3,反推得交换前的球编号为2,1,3
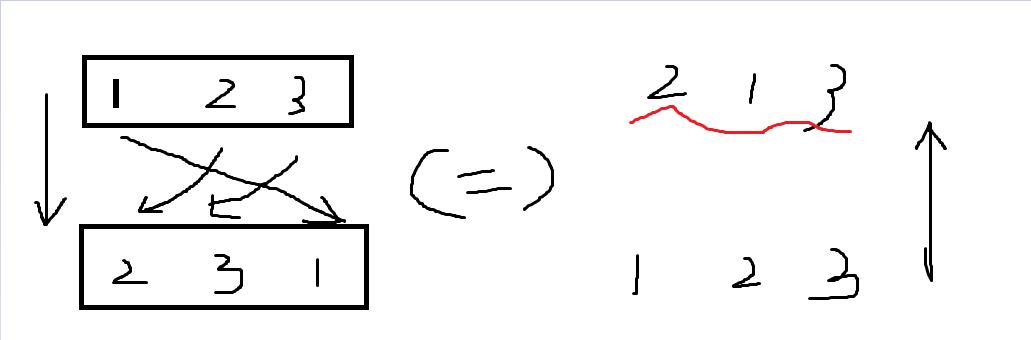
这样就抵消掉询问区间[l,r],l-1以前交换的效果了,重新编号后,将r时的小球状态还原成重新编号的球即可
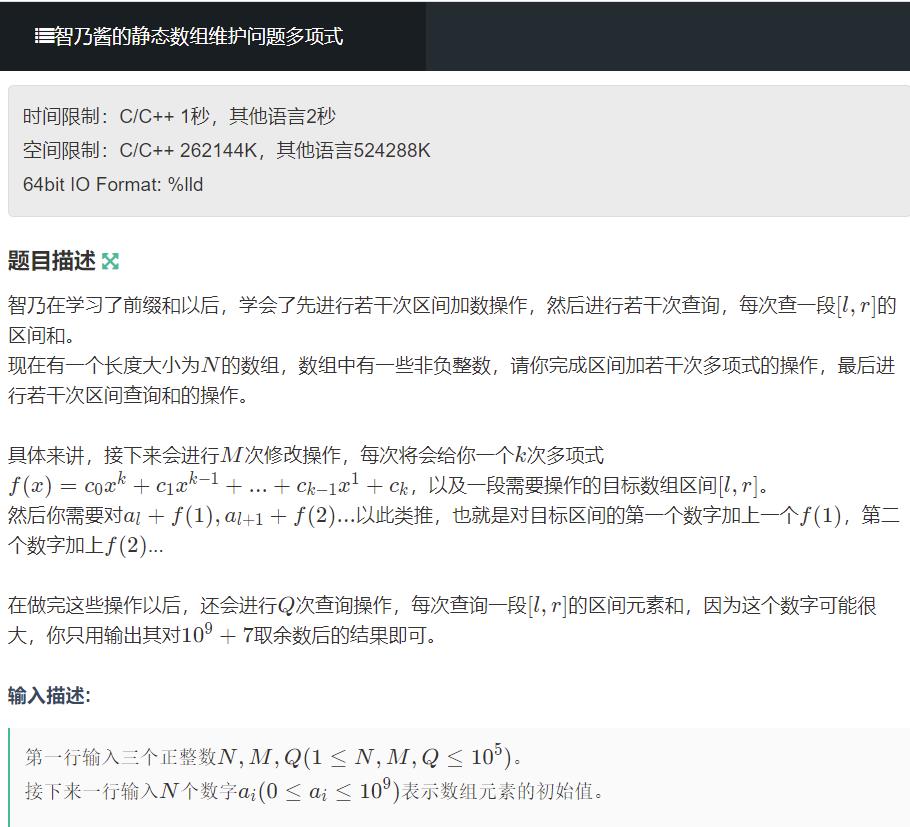

思路:群论
有个定理,最高次项为n次的n阶多项式做n+1阶差分后余项为常数,前后缀和区间加多项式
差分的最本质就可以从区间加减多项式体现出来了
对[l,r]加f(x)操作,需要对位置r+1进行减f(x+r-l+1)的操作,相当于一次差分的++--操作
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#include <list>
#include <queue>
#include <vector>
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <deque>
using namespace std;
typedef long long ll;
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define scd(v) scanf("%d",&v)
#define scdd(a,b) scanf("%d %d",&a,&b)
#define endl "\\n"
#define IOS ios::sync_with_stdio(false)
#define pb push_back
#define all(v) v.begin(),v.end()
#define int long long
#define odd(x) x&1
#define mst(v,a) memset(v,a,sizeof(v))
#define lson p<<1 ,l,mid
#define rson p<<1|1,mid+1,r
#define ls p<<1
#define rs p<<1|1
#define fi first
#define se second
#define pii pair<int,int>
#define inf 0x7f7f7f7f
const int N=1e5+500;
const int mod=1e9+7;
int n,m,l,r,k,q;
int a[N];
int b1[N],b2[N],ki[N];
void D(int a[] ,int len ,int cnt)//差分数组
{
while( cnt-- )
{
_rep(i,len,1)
{
a[i] = a[i] - a[i-1];
a[i] = (a[i]+mod)%mod;
}
}
}
void P(int a[] ,int len ,int cnt)//差分数组
{
while( cnt-- )
{
_for(i,1,len)
{
a[i] = a[i] + a[i-1];
a[i] = (a[i])%mod;
}
}
}
int f(int x, int a[] ,int k)
{
int ans=0;
int base=1;
_for(i,0,k)
{
ans += base * ki[i], ans %=mod;
base *= x ,base%=mod;
}
return ans;
}
int g(int x, int a[] ,int k ,int l, int r)
{
return (mod - f(x+r-l+1,a,k))%mod;
}
signed main()
{
//!!//
// freopen("data.txt","r",stdin);
//!!
IOS;
cin>>n>>m>>q;
_for(i,1,n) cin>>a[i];
D(a,n,6);
while( m-- )
{
cin>>l>>r>>k;
_rep(i,k,0)
{
cin>>ki[i];
}
_for(i,1,10)//差分前十项就够了
{
b1[i] = f(i,ki,k);
b2[i] = g(i,ki,k,l,r);
}
//k最大5,差分六次即可
D(b1,10,6);
D(b2,10,6);
_for(i,1,10)
{
a[l+i-1] += b1[i] , a[l+i-1]%=mod;
a[r+i] += b2[i] , a[r+i]%mod;
}
}
P(a,n,7);//还原差分且求前缀和
while( q-- )
{
int l,r;cin>>l>>r;
cout<<(a[r]-a[l-1]+mod)%mod<<endl;
}
}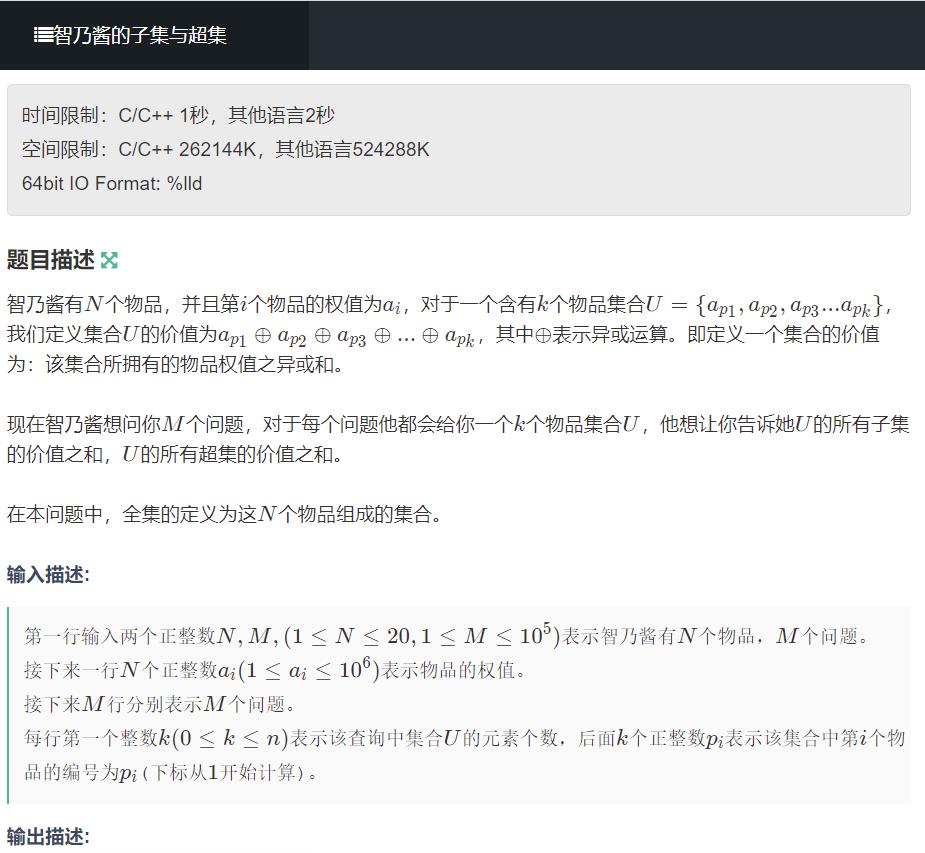

思路:sosdp
怎么前缀和处理所有子集和超集呢
如果只有二维的话,我们可以借鉴最大子矩阵的容斥,简单画个图带过了
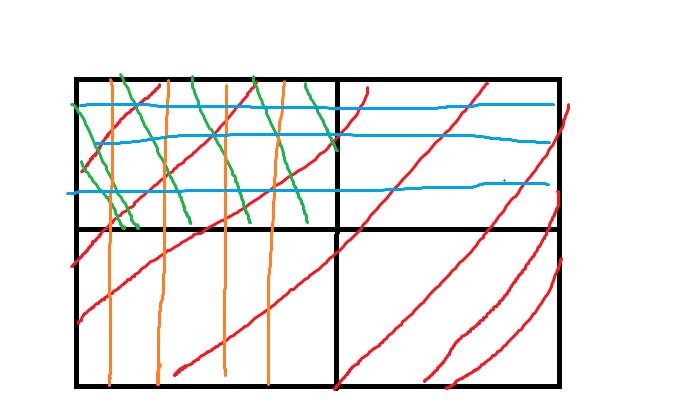
(聚丑的图QAQ)
ans = 红 - 橙 - 蓝 + 绿
再高维,那容斥要命了,引入sosdp子集前缀和
以上是关于前缀和思想的主要内容,如果未能解决你的问题,请参考以下文章