3.剑指Offer --- 高质量的代码

Posted 2021-09-12 enlyhua

第3章 高质量的代码 
3.1 面试官谈代码质量 
	精度原因不能判断两个小数是否相等。

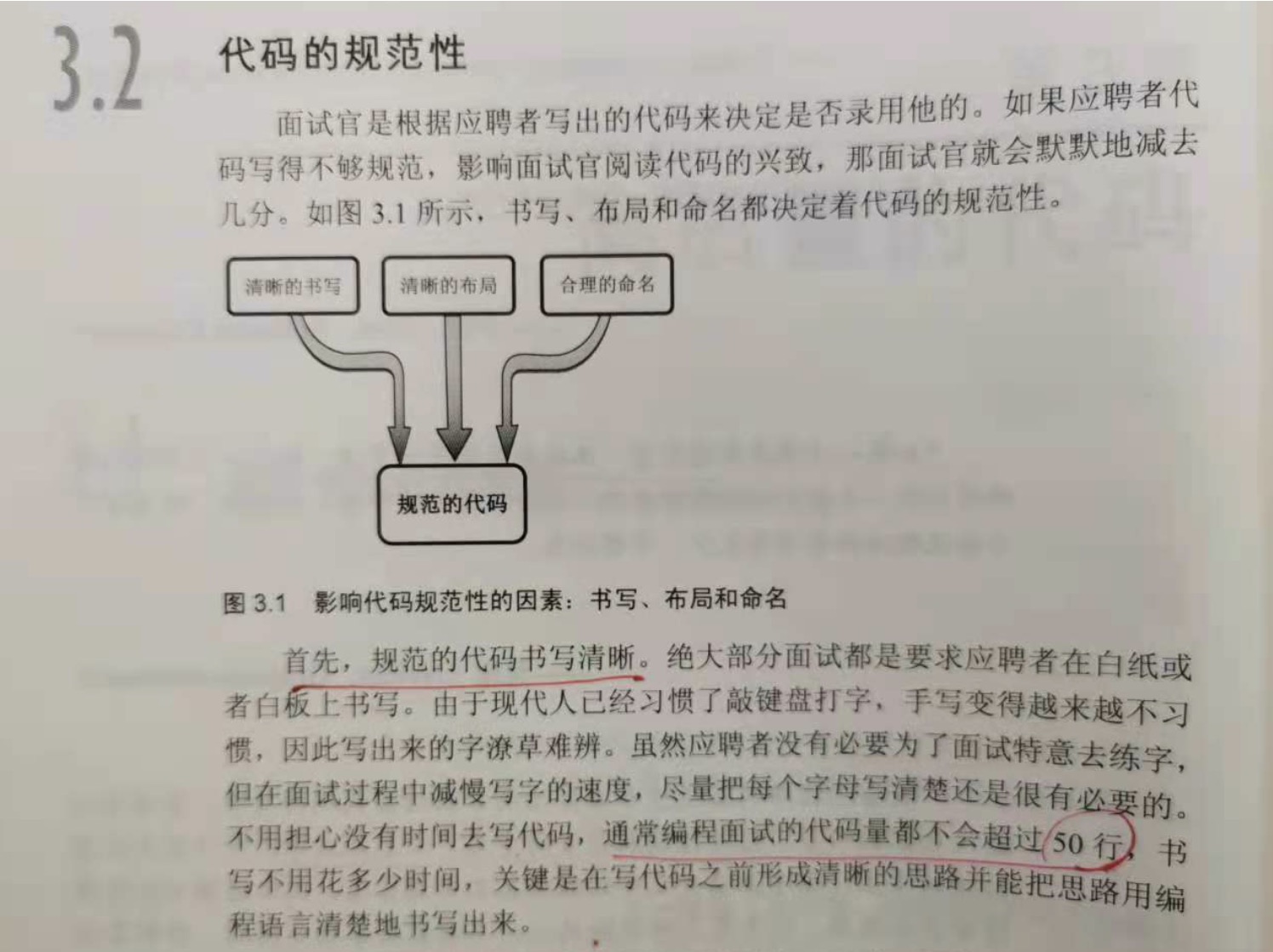
3.2 代码的规范性 
	1.首先，书写清晰
	2.其次，布局清晰
	3.最后，命名合理

3.3 代码的完整性 
	1.从3个方面确保代码的完整性
		a) 功能测试
		b) 边界测试
		c) 负面测试

	2.3种错误处理方法
		a) 返回值
		b) 全局变量
		c) 异常

面试题11：数值的整数次方
	题目：实现函数 doulbe Power(double base, int exponent)，求base的exponent次方。不得使用库函数，同时不需要考虑大数问题。

	自以为是的解法：
double Power(doulbe base, int exponent)
{
	double result = 1.0;

	for (i = 1; i <= exponent; i++) {
		result *= base;
	}

	return result;
}
	
	全面但不够高效的解法：
		我们知道当指数为负数的时候，可以先对指数求绝对值，然后算出次方的结果后再取倒数。如果底数(base)是0且指数是负数的时候，怎么办？

bool g_InvalidInput = false;

double Power(double base, int exponent)
{
	g_InvalidInput = false;

	//底数为0，且指数为负的情况
	if (equal(base, 0.0) && expoent < 0) {
		g_InvalidInput = true;
		return 0.0;
	}

	//求指数的绝对值
	unsigned int absExponent = (unsigned int)(exponent);
	if (exponent < 0) {
		absExponent = (unsigned int) (-exponent);
	}

	double result = PowerWithUnsignedExpoent(base, absExponent);

	//如果指数为负数，求倒数
	if (exponent < 0) {
		result = 1.0/result;
	}

	return result;
}
	
double PowerWithUnsignedExpoent(double base, unsigned int expoent)
{
	double result = 1.0;

	for (int i = 1; i <= exponent; i++) {
		result *= base;
	}

	return result;
}

//判断两个小数是否相等，只能判断它们只差的绝对值是不是在一个很小的范围内
bool equal(doulbe numl, doulbe num2)
{
	if ( (num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001) ) {
		result true;
	} else {
		result false;
	}
}
	
	全面又高效的解法:
		如果输入的指数为32，我们就需要循环31次。可以换一种思路：我们的目标是求出一个数字的32次方，如果我们已经知道16次方，那么只要在16次方的
	基础上再平方一次即可。	
		a^n = {
			a^(n/2) * a^(n/2);
			a^(n-1/2) * a^(n-1/2) * a; 
		};

double PowerWithUnsignedExpoent(double base, unsigned int exponent)
{
	if (exponent == 0) {
		return 1;
	} 

	if (exponent == 1) {
		return base;
	}

	//右移代替除法
	double result = PowerWithUnsignedExpoent(base, exponent >> 1);
	result *= result;

	//用 与运算判断奇偶，如果是奇数，再乘以base
	if (exponent & 0x1 == 1) {
		result *= base;
	}

	return result;
}

面试题12：打印1到最大的n位数
	题目：输入数字n，按顺序打印从1最大的n位十进制数。比如输入3，打印输出1，2，3 一直到最大的3位数即999.

	跳进面试官陷进：
void Print1ToMaxOfNDigits_1(int n)
{
	int number = 1;
	int i = 0;

	while (i++ < n) {
		number *= 10;
	}

	for (i = 1; i < number; i++) {
		printf("%d \\t", i);
	}
}
	缺点：没有规定n的范围。当输入n很大的时候，我们求最大的n位数是不是用int 或者 long long 都会溢出。也就是没有考虑大数问题。

	在字符串上模拟数字加法的解法：
void Print1ToMaxOfNDigits(int n)
{
	if (n <= 0) {
		return;
	}

	char* number = new char[n+1];

	//初始化
	memset(number, '0', n);
	number[n] = '\\0';

	//Increment 实现在 number 上加1
	while (!Increment(number)) {
		PrintNumber(number);
	}

	delete []number;
}

//我们注意到只有对 '999..99' 加1的时候，才会在第一个字符(下标为0)的基础上产生进位，而其他所有情况都不会在第一个字符上产生进位。
//因此当我们发现在加1时产生第一个字符进位，就已经是最大的n位数，此时Increment 返回true。如何在每一次加1后迅速判断是不是到了最大的n
//位数是本题的一个小陷阱。
void Increment(char* number)
{
	bool isOverflow = false;
	int nTakeOver = 0;
	int nLength = strlen(number);

	for (int i = nLength - 1; i >= 0; i--) {
		int nSum = number[i] - '0' + nTakeOver;
		if (i == nLength - 1) {
			nSum ++;
		}

		if (nSum >= 10) {
			if (i == 0) {
				isOverflow = true;
			} else {
				nSum -= 10;
				nTakeOver = 1;
				number[i] = '0' + nSum;
			}
		} else {
			number[i] = '0' + nSum;
			break;
		}
	}

	return isOverflow;
}

void PrintNumber(char* number)
{
	bool isBeginning0 = true;
	int nLength = strlen(number);

	for (int i = 0; i < nLength; i++) {
		if (isBeginning0 && number[i] != '0') {
			isBeginning0 = false;
		}

		if (!isBeginning0) {
			printf("%c", number[i]);
		}
	}
}

	
	把问题转换成数字排列的解法，递归让代码更简洁:
void Print1ToMaxOfDigits(int n)
{
	if (n <= 0) 
		return;

	char* number = new char[n + 1];
	number[n] = '\\0';

	for (int i = 0; i < 10; i++) {
		number[0] = i = '0';
		Print1ToMaxOfDigitsRecursively(number, n, 0);
	}

	delete []number;
}

void Print1ToMaxOfDigitsRecursively(char* number, int length, int index)
{
	if (index == length - 1) {
		PrintNumver(number);
		return;
	}

	for (int i = 0; i < 10; i++) {
		number[index + 1] = i + '0';
		Print1ToMaxOfDigitsRecursively(number, length, index + 1);
	}
}

	
面试题13：在O(1)时间删除链表结点
	题目：给定单向链表的头指针和一个结点指针，定义一个函数在O(1)时间删除该结点。链表结点与函数的定义如下：
struct ListNode {
	int m_nValue;
	ListNode* m_pNext;
};
	
void DeleteNode(ListNode** pListHead, ListNode* pToBeDeleted);
	
	把i的结点j的内容复制到结点i，接下来再把结点i的m_pNext指向j的下一个结点之后删除结点j。这种方法不需要遍历链表上结点i前面的节点；
需要注意的是，如果要删除的结点位于链表的尾部，那么它没有下一个结点。这时候需要遍历。

void DeleteNode(ListNode** pListHead, ListNode* pToBeDeleted)
{
	if (!pListhead || !pToBeDeleted) 
		return;

	//要删除的结点不是尾结点
	if (pToBeDeleted->m_pNext != null) {
		ListNode* pNext = pToBeDeleted->m_pNext;
		pToBeDeleted->m_nValue = pNext->m_nValue;
		pToBeDeleted->m_pNext = pNext->m_pNext;

		delete pNext;
		pNext = null;

	//链表只有一个结点，删除头结点(也是尾结点)
	} else if (*pListHead == pToBeDeleted) {
		delete pToBeDeleted;
		pToBeDeleted = null;
		*pListHead = null;

	//链表中有多个结点，删除尾结点，需要遍历
	} else {
		ListNode* pNode = *pListHead;
		while (pNode->m_pNext != pToBeDeleted) {
			pNode = pNode->m_pNext;
		}

		pNode->m_pNex = null;
		delete pToBeDeleted = null;
		pToBeDeleted = null;
	}
}


面试题14：调整数组顺序使得奇数位于偶数前面
	题目：输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

	只完成基本功能的解法，仅适用于初级程序员：
		我们在扫描这个数组的时候，如果发现有偶数出现在奇数前面，我们可以交换它们的顺序，交换之后就符合要求了。

		因此，我们维护两个指针，第一个指针初始化时指向数组的第一个数字，它指向后移动；第二个指针初始化时指向数组的最后一个数字，它只向
	前移动。在两个指针相遇之前，第一个指针总是位于第二个指针的前面。如果第一个指针是偶数，并且第二个指针指向的数字是奇数，就交换之。

void ReorderOddEven(int *pData, unsigned int length)
{
	if (pData == null || length == 0) {
		return;
	}

	int *pBegin = pData;
	int *pEnd = pData + length - 1;

	while (pBegin < pEnd) {
		
		//向后移动pBegin,直到指向偶数
		while (pBegin < pEnd && (*pEnd & 0x1) != 0) {
			pBegin++;
		}

		//向前移动pEnd,直到指向奇数
		while (pBegin < pEnd && (*pEnd & 0x1) == 0) {
			pEnd--;
		}

		if (pBegin < pEnd) {
			int temp = *pBegin;
			*pBegin = *pEnd;
			*pEnd = temp;
		}
	}
}

	考虑可扩展性的解法，秒杀offer:

void Reorder(int* pData, unsigned int length, bool (*func) (int))
{
	if (pData == null || length == 0) 
		return;

	int* pBegin = pData;
	int* pEnd = pData + length - 1;

	while (pBegin < pEnd) {
		while (pBegin < pEnd && !func(*pBegin)) {
			pBegin++;
		}

		while (pBegin < pEnd && func(*pEnd)) {
			pEnd--;
		}

		if (pBegin < pEnd) {
			int temp = *pBegin;
			*pBegin = *pEnd;
			*pEnd = temp;
		}
	}
}

bool isEven(int n)
{
	return (n & 1) == 0;
}	

void ReorderOddEven(int* pData, unsigned int length)
{	
	Reorder(pData, length, isEven);
}


3.4 代码的鲁棒性 
	鲁棒性是指程序能够判断输入是否符合要求，并对不符合要求的输入予以合理的处理。容错性是鲁棒性的一个重要体现。提高代码鲁棒性的有效途径是
进行防御性编程。防御性编程是一种编程习惯，是指预见在什么地方可能会出现的问题，并为这些可能会出现的问题制定处理方式。
	
	在面试的时候，最简单也最实用的防御性编程就是在函数入口添加代码以验证用户输入是否符合要求。

面试题15：链表中倒数第k个结点
	题目：输入一个链表，输出该链表中倒数第k个结点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾结点是倒数第1个结点。例如一个链表有6
个结点，从头结点开始它们的值依次是1，2，3，4，5，6.这个链表的倒数第三个结点是值4的结点。
	
	链表结点定义如下：
struct ListNode {
	int m_nValue;
	ListNode* m_pNext;
};
	
	为了得到倒数第k个结点，很自然的想法是先走到链表尾部，然后从尾部回溯k步。可是我们从链表结点的定义可以看出来链表是单向的，单向链表的结点
只有从前往后的指针而没有从后往前的指针，因此行不通。
	
	既然不能从尾结点开始遍历这个链表，还是把思路回到头结点上来。假设整个链表有n个结点，那么倒数第k个结点就是从头开始的第n-k+1个结点。如果
我们能够得到链表中结点的个数n，那么我们只要从头往后走n-k+1步就可以了。如何得到结点个数n? 这个不难，只需要从头遍历链表，累加1。也就是说我们需要
遍历两次链表。
	
	为了实现只遍历一次链表就能找到倒数第k个结点，我们可以定义两个指针。第一个指针从链表的头指针开始遍历向前走k-1，第二个指针保持不动；从第k步
开始，第二个指针也开始从链表的头指针开始遍历。由于两个指针的距离保持k-1，当第一个(走在前面的)指针到达链表的尾部时，第二个指针(走在后面的)指针
正好是倒数第k个结点。
	
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k)
{
	ListNode* pAhead = pListHead;
	ListNode* pBehind = null;

	for (unsigned int i = 0; i < k - 1; i++) {
		pAhead = pAhead->m_pNext;
	}

	pBehind = pListHead;

	while (pAhead->m_pNext != null) {
		pAhead = pAhead->m_pNext;
		pBehind = pBehind->m_pNext;
	}

	return pBehind;
}

	上面程序需要考虑3个方面的鲁棒性：
		a) pListHead 为空指针；
		b) 链表的结点数小于k;
		c) 输入的k为0；

修改后的代码:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k)
{
	if (pListHead == null || k == 0) {
		return null;
	}

	ListNode* pAhead = pListHead;
	ListNode* pBehind = null;

	for (unsigned int i = 0; i < k - 1; i++) {
		if (pAhead->m_pNext != null) {
			pAhead = pAhead->m_pNext;
		} else {
			return null;
		}
	}

	pBehind = pListHead;

	while (pAhead->m_pNext != null) {
		pAhead = pAhead->m_pNext;
		pBehind = pBehind->m_pNext;
	}

	return pBehind;
}

	相关题目：
		1.求链表的中间结点。如果链表中结点总数为奇数，返回中间结点。如果结点总数为偶数，返回中间结点的任意一个。为了解决这个问题，我们也可以
	定义两个指针，同时从链表的头结点出发，一个指针走一步，一个指针走两步。当走的快的指针到达链表末尾的时候，走的慢的指针正好在链表中间。

		2.判断一个单向链表是否有环。定义两个指针，一个走1步，一个走2步。如果走的快的指针追上了走的慢的，那么就是有环。如果走的快的指针走到了
	链表的末尾都没追上第一个指针，那就是没有环。

	举一反三：
		当我们用一个指针遍历链表不能解决问题的时候，可以用2个指针。让其中一个走的快点。

面试题16：反转链表
	题目：定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。链表节点定义如下：
struct ListNode {
	int m_nKey;
	ListNode* m_pNext;
};
	

ListNode* ReverseList(ListNode* pHead)
{
	ListNode* pReverseHead = null;
	ListNode* pNode = pHead;
	ListNode* pPrev = null;

	while (pNode != null) {
		ListNode* pNext = pNode->m_pNext;

		if (pNext == null) {
			pReversedHead = pNode;
		}

		pNode->m_pNext = pPrev;
		pPrev = pNode;
		pNode = pNext;
	}

	return pReversedHead;
}	


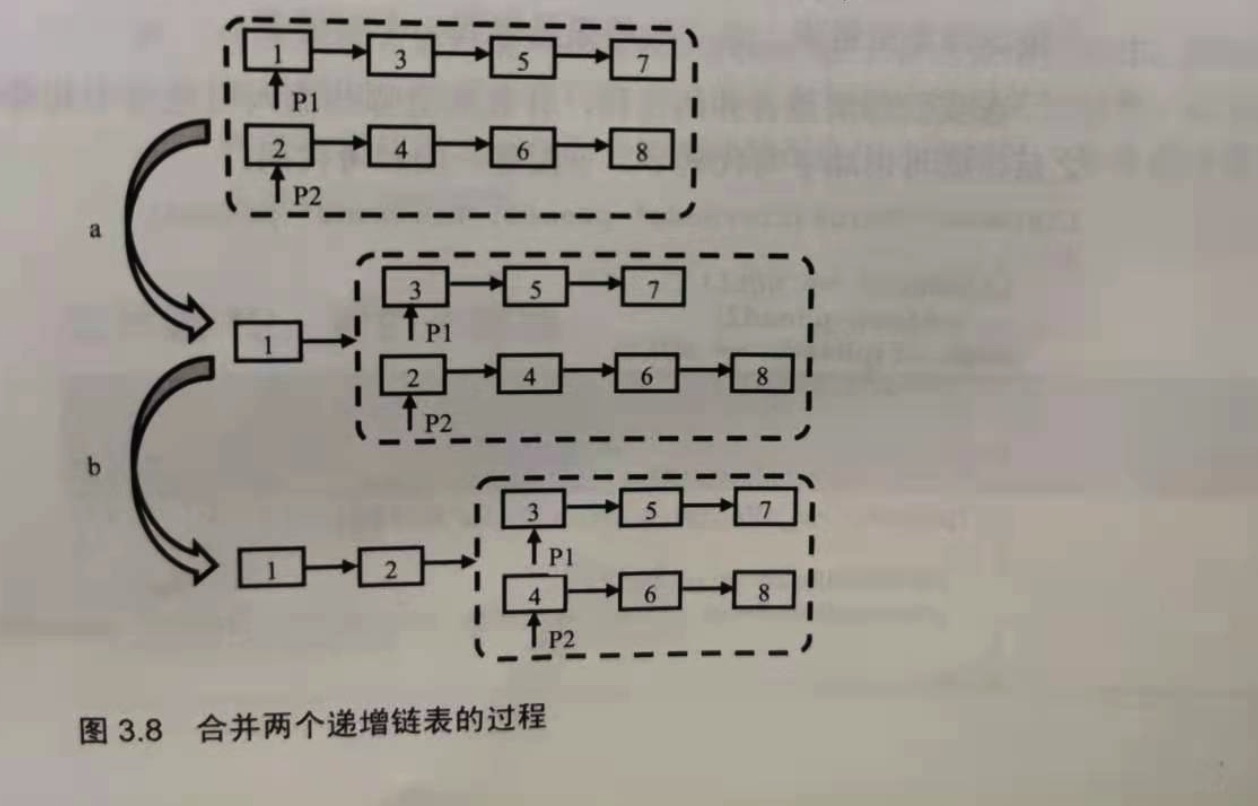
面试题17：合并两个排序的链表
	题目：输入两个递增排序的链表，合并这2个链表并使新链表中的结点仍然是递增排序的。
struct LideNode {
	int m_nValue;
	ListNode* m_pNext;
};
	
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
	if (pHead1 == null) {
		return pHead2;
	} else if (pHead2 == null) {
		return pHead1;
	}

	ListNode* pMergeHead = null;

	if (pHead1->m_nValue < pHead2->m_nValue) {
		pMergeHead = pHead1;
		pMergeHead->m_pNext = Merge(pHead1->m_pNext, pHead2);
	} else {
		pMergeHead = pHead2;
		pMergeHead = m_pNext = Merge(pHead1, pHead2->m_pNext2);
	}

	return pMergedHead;
}


面试题18：树的子结构
	题目：输入两颗二叉树A和B，判断B是不是A的子结构。二叉树的定义如下：
struct BinaryTreeNode {
	int m_nValue;
	BinaryTreeNode* m_pLeft;
	BinaryTreeNode* m_pRight;
};
	
	分析：要查找树A中是否包含存在和树B一样的子树，我们可以分成两步：1.在树A中找到和树B根结点一样的结点R；2.判断树A中以R为根结点的子树
  是不是包含和树B一样的结构。

bool HasSubTree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
	bool result = false;

	if (pRoot1 != null && pRoot2 != null) {
		if (pRoot1->m_nValue == pRoot2->m_nValue) {
			result = DoesTree1HaveTree2(pRoot1, pRoot2);
		}

		if (!result) {
			result = HasSubtree(pRoot1->m_pLeft, pRoot2);
		}

		if (!result) {
			result = HasSubtree(pRoot1->m_pRight, pRoot2);
		}
	}

	return result;
}
	
	上述代码中，我们递归调用 HasSubtree 遍历二叉树A。如果发现某一结点的值和树B的头结点的值相同，则调用 DoesTree1HaveTree2，做第二步判断。
	
	第二步判断树A中以R为根结点的子树是不是树B具有相同的结构。同样，我们也可以用递归来考虑:
		如果结点R的值和树B的根结点不相同，则以R为根结点的子树和树B肯定不具有相同的结点；如果他们的值是相同的，则递归判断它们各自的左右结点的值
	是不是相同。递归终止的条件是我们达到了树A或者树B的叶节点。

bool DoesTree1HaveTree2(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
	if (pRoot2 == null) {
		return true;
	}

	if (pRoot1 == null) {
		return false;
	}

	if (pRoot1->m_nValue != pRoot2->m_nValue) {
		return false;
	}

	return DoesTree1HaveTree2(pRoot1->m_pLeft, pRoot2->m_pLeft) && DoesTree1HaveTree2(pRoot1->m_pRight, pRoot2->m_pRight);
}

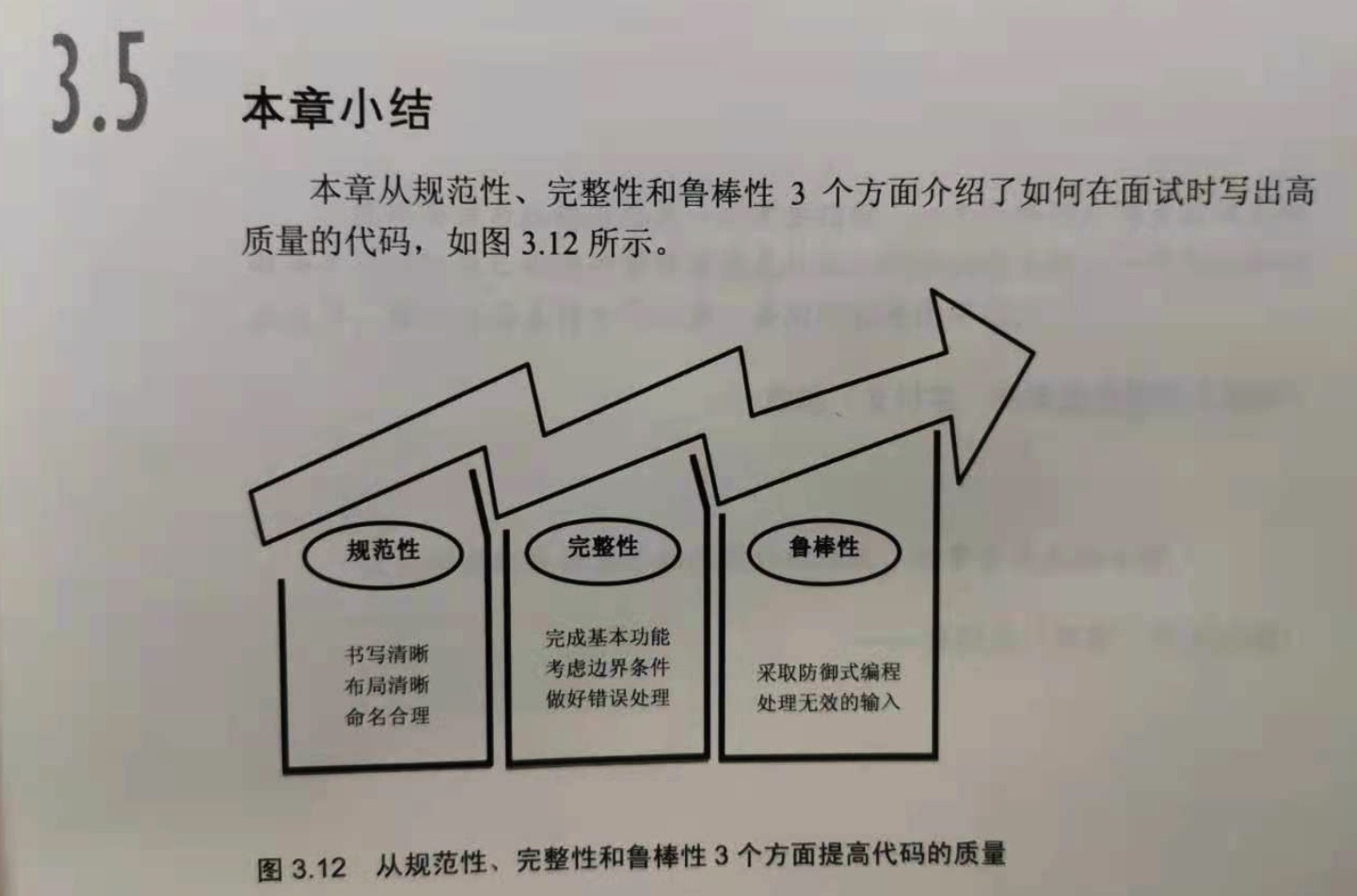
	总结：
		1.规范性
			a) 书写清晰
			b) 布局清晰
			c) 命名合理
		2.完整性
			a) 完成基本功能
			b) 考虑边界条件
			c) 做好错误处理
		3.鲁棒性
			a) 采用防御性编程
			b) 处理无效输入