第二章 | 分类问题 | F1-score | ROC曲线 | 精准率召回率 | tensorflow2.6+sklearn | 学习笔记

Posted 2021-09-12 冰_墩_墩

tags:

1. 学习目标

本章以mnist数据集为例，研究

二元分类器
多元分类器
精准率,召回率
F1_score
ROC曲线

2. 数据集介绍

很普通的入门级数据集——mnist手写数字识别
看看其中的一张图片

# 展示图片
def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    plt.axis("off")
some_digit = X[36000]
plot_digit(X[36000].reshape(28,28))

# 更好看的图片展示
def plot_digits(instances,images_per_row=10,**options):
    size=28
    # 每一行有一个
    image_pre_row=min(len(instances),images_per_row)
    images=[instances.reshape(size,size) for instances in instances]
#     有几行
    n_rows=(len(instances)-1) // image_pre_row+1
    row_images=[]
    n_empty=n_rows*image_pre_row-len(instances)
    images.append(np.zeros((size,size*n_empty)))
    for row in range(n_rows):
        # 每一次添加一行
        rimages=images[row*image_pre_row:(row+1)*image_pre_row]
        # 对添加的每一行的额图片左右连接
        row_images.append(np.concatenate(rimages,axis=1))
    # 对添加的每一列图片 上下连接
    image=np.concatenate(row_images,axis=0)
    plt.imshow(image,cmap=mpl.cm.binary,**options)
    plt.axis("off")

plot_digits(x_train_[:25],images_per_row=5)
plt.show()

3. 二元分类案例

我们用一个二元分类的例子，来说明分类器的评价指标应该怎么样决定

3.1 加载数据

mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train_ = x_train.reshape(60000,784)
x_test_ = x_test.reshape(10000,784)

判断一个数字是不是5，如果是5 就是True，不是5 就是False
我们来基于mnist，制作二元分类数据，将标签是5的改为True，不是5的改为False
如下所示：

y_train_5 = (y_train == 5)

效果：

3.2 随机梯度下降(SGD)模型

建立一个随机梯度下降的模型，将图片训练集和自己建立的目标集放入模型中训练，然后考虑模型的评价方法

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(x_train_,y_train_5)
res = sgd_clf.predict([x_train_[0]])
print(res)

3.3 评估分类器

评估分类器比评估回归器要困难的多
使用交叉验证评估随机梯度下降模型

    res = cross_val_score(sgd_clf,x_train,y_train_5,cv=3,scoring='accuracy')
    print(res)

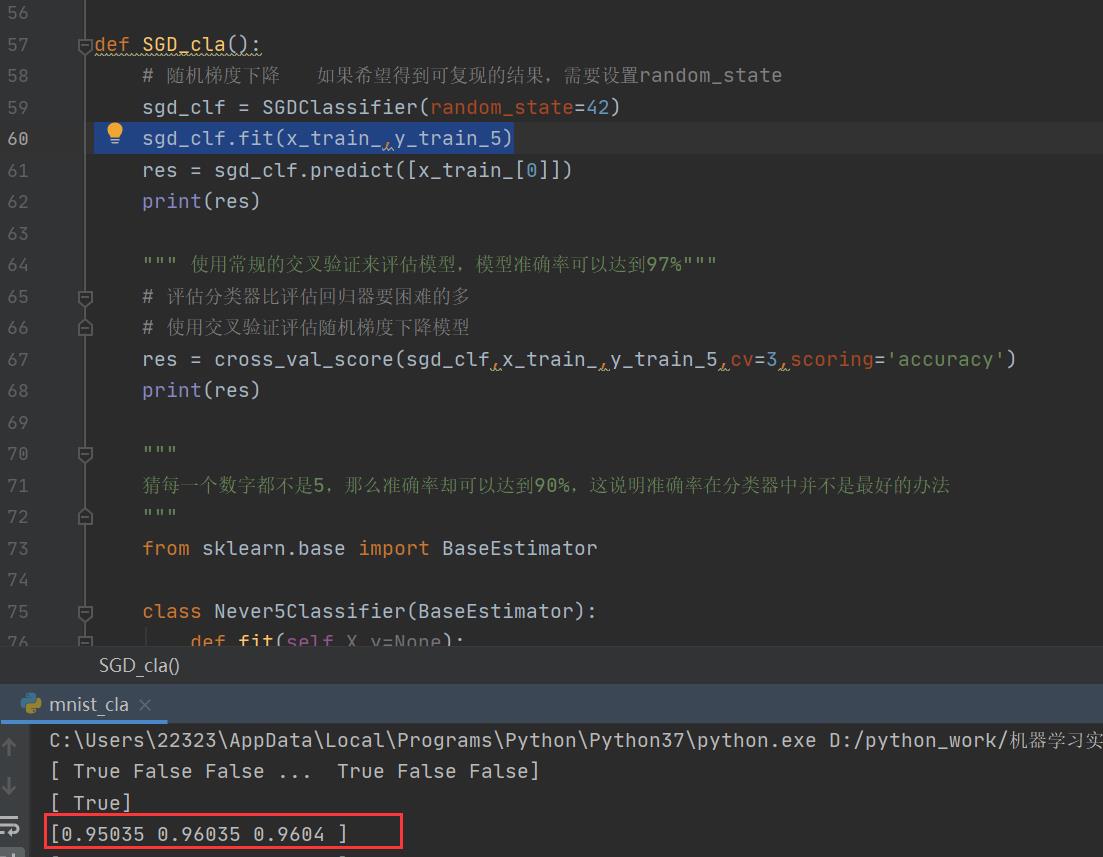
可以发现：
使用常规的交叉验证来评估模型，模型准确率可以达到97%。

一切看起来都很顺利吧，现在有这样一个问题，如果我们建立一个新的分类器，我们这个分类器猜测每一个数字都不是5，那这10个数字，不是5的可能性是90%，我们可以说模型效果很好吗？如下：

from sklearn.base import BaseEstimator

    class Never5Classifier(BaseEstimator):
        def fit(self,X,y=None):
            return self
        def predict(self,X):
            # print(len(X))
            # print(np.zeros((len(X), 1),dtype=np.int))
            # 返回[[False]]   不管是什么结果，都会返回false
            return np.zeros((len(X),1),dtype=bool)

    never_5_clf = Never5Classifier()
    res = cross_val_score(sgd_clf,x_train_,y_train_5,cv=3,scoring='accuracy')
    print(res)

跟猜测一样，分类器猜测每一个数字都不是5，使用交叉验证得到的结果，准确率在90%左右，这并不能说明模型是一个好的模型

下面就来到评估分类器的一个好方法 —— 混淆矩阵

3.4 混淆矩阵

cross_val_predict 和 cross_val_score的区别，一个是返回分数，一个数返回预测结果。我们继续回到之前97%准确率的随机梯度下降的二元分类器，使用新的评估方法进行评估

	# 交叉验证返回最好预测
	from sklearn.model_selection import cross_val_predict
    y_train_pred = cross_val_predict(sgd_clf,x_train_,y_train_5,cv=3)
 	  # 返回的是预测结果
    print(y_train_pred)

获取混淆矩阵

# 混淆矩阵
from sklearn.metrics import confusion_matrix

# 第一个参数是标签，第二个参数是预测值
res = confusion_matrix(y_train_5,y_train_pred)
print(res)

结果：

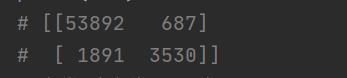
上面的结果表明：第一行所有’非5’(负类)的图片中,有53892被正确分类(真负类)，687错误分类成了5(假负类)；第二行表示所有’5’（正类）的图片中，有1891错误分类成了非5(假正类)，有3530被正确分类成5(真正类)

二元分类器的混淆矩阵如下分布：
负类真负类假正类
正类假负类真正类
完美的二分类器，只有左上和右下有非零值

3.5 精准率和召回率

接下来就可计算精准率和召回率

# 精度和召回率
from sklearn.metrics import precision_score, recall_score
# f1 score
from sklearn.metrics import f1_score

print(precision_score(y_train_5,y_train_pred))  # 3530 / (3530 + 687)
print(recall_score(y_train_5,y_train_pred))     # 3530 / (3530 + 1891)

 # f1-score  当召回率和精度都很高的时候，分类器才会得到较高的 f1-score
 print(f1_score(y_train_5,y_train_pred))

我们可以看到，这个5-检测器，并没有表面那么高的准确率，大多时候，它说一张图片为5时，只有83%的概率是准确的，并且也只有75%的5被检测出来了
我们可以将精度和召回率组合成单一的指标，称为F1分数。要计算F1分数

只需要调用f1_score()即可，代码如上

F1分数对那些具有相近的精度和召回率的分类器更为有利。这不一定一直符合预期，因为在某些情况下，我们更关心精度，而另一些情况下，我们可能真正关系的是召回率。

精准率和召回率权衡

例如：假设训练一个分类器来检测儿童可以放心观看的视频，那么我们可能更青睐那种拦截了好多好视频(低召回率),但是保留下来的视频都是安全(高精度)的分类器；
反过来说，如果你训练一个分类器通过图像监控来检测小偷:你大概可以接受精度只有30%，只要召回率能达到99%。(当然，安保人员会接收到一些错误的警报，但是几乎所有的窃贼都在劫难逃)
遗憾的是，鱼和熊掌不可兼得：我们不能同时增加精度并减少召回率，反之亦然，这称为精度/召回率权衡

在分类中，对于每个实例，都会计算出一个分值，同时也有一个阈值，大于为正例，小于为负例。通过调节这个阈值，可以调整精度和召回率。

提高阈值可以提高精度，降低召回率；降低阈值会提高召回率，降低精度
这里使用cross_val_predict返回每个数字的决策分数

# 注意 method='decision_function'
    y_scores = cross_val_predict(sgd_clf,x_train_,y_train_pred,cv=3,method='decision_function')

使用precision_recall_curve()来计算所有可能的精度召回率阈值

from sklearn.metrics import precision_recall_curve
precisions,recalls,thresholds = precision_recall_curve(y_train_5,y_scores)
print("阈值：",thresholds)
print("精度：",precisions)
print("召回率：",recalls)

画出 precisions,recalls,thresholds 之间的变化关系：

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.xlabel("Threshold", fontsize=16)
    plt.title("精度和召回率VS决策阈值", fontsize=16)
    plt.legend(loc="upper left", fontsize=16)
    plt.ylim([0, 1])

plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()

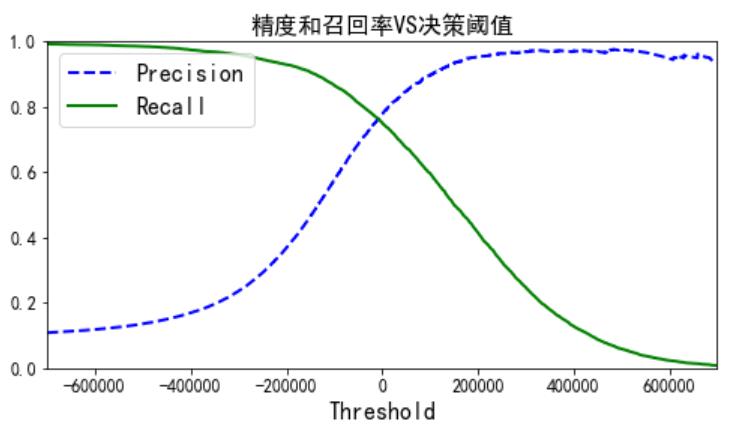
假设我们要建立一个90%精度的模型

threshold_90_precision = thresholds[np.argmax(precisions > 0.9)]
print("精度为0.9的阈值是：",threshold_90_precision)   # 1062

# 根据0.9精度的阈值进行新的预测，将低于阈值的，强制变为假，高于阈值的变为真
y_train_pred_90 = (y_scores >= threshold_90_precision)

# 这里第一个参数是标签，第二个参数是预测结果
print("新的预测精度为：",precision_score(y_train_5,y_train_pred_90))  # 这里就会很轻松的得到一个90%精度的模型，但是召回率很很低
print("新的召回率是：",recall_score(y_train_5, y_train_pred_90))

我们这样很容易就得到一个90%精度的分类器，但是召回率会相对变低。

我们可以在代码预测部分，通过这种调整阈值的方法，来提高精度或者召回率

3.6 ROC曲线 ROC_AUC分数

还有一种经常与二元分类器一起使用的工具，叫做受试者工作特征曲线(简称ROC)。它与精度/召回率曲线非常相似，但绘制的不是精度和召回率，而是真正类率(召回率的另一种称呼)和假正类率(FPR)。FPR是被错误分为正类的负类实例比率。它等于1-真负类率(TNR)，后者正是被正确分类为负类的负类实例比率，也称为奇异度。因此ROC曲线绘制的是灵敏度和(1-奇异度)的关系

# ROC曲线
from sklearn.metrics import roc_curve

# 使用
fpr,tnr,thresholds = roc_curve(y_train_5,y_scores)

 plot_roc_curve(fpr,tnr)
 plt.show()

# 计算ROC_AUC分数
from sklearn.metrics import roc_auc_score

 # 一个完美的分类器，AUC 和 ROC都等于1，纯随机分类器 AUC和ROC 等于0.5
 print(roc_auc_score(y_train_5,y_scores))

3.7 随机森林

训练一个随机森林分类器，并计算ROC和ROC AUC分数，与SGD做对比

# 具体RF的原理
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=10, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)


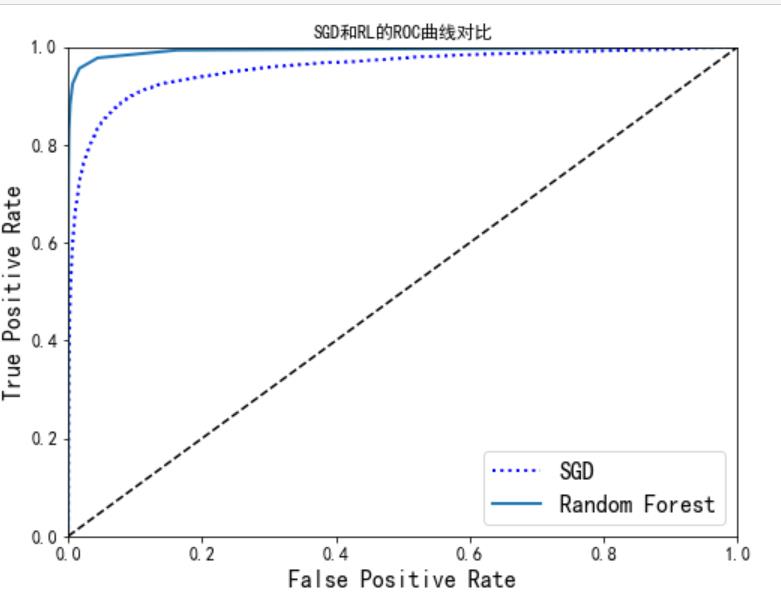
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.title("SGD和RL的ROC曲线对比")
plt.legend(loc="lower right", fontsize=16)
plt.show()

roc_auc_score(y_train_5, y_scores_forest)
# 0.9931243366003829

# 测量精度和召回率
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)
# 0.9852973447443494

recall_score(y_train_5, y_train_pred_forest)
# 0.8282604685482383

可以看出，随机森林分类器是明显优于随机梯度下降的

4. 多元分类案例

二元分类器在两个类别中区分，而多类别分类器(也称为多项分类器),可以区分两个以上的类别。
随机森林算法和朴素贝叶斯分类器可以直接处理多个类别。
也有一些严格的二元分类器，比如支持向量分类器或线性分类器。
但有多种策略，可以让我们用几个二元二类器实现多类别分类的目的
例如：

我们可以训练0-9的10个二元分类器组合，那个分类器给的高，就分为哪一类，这称为一对多(OvA)策略 one vs all
另一种方法，是为每一对数字训练一个二元分类器:一个用来区分0-1，一个区分0-2，一个区分1-2，依次类推。这称为一对一(OvO)策略，解决N分类，需要(N)*(N-1)/2分类器，比如MNIST问题，需要45个分类器。OvO的主要优点在于每个分类器只需要用到部分训练集对其必须区分的两个类别进行训练。 one vs one

有些算法(例如支持向量机算法)，在数据规模增大时，表现糟糕，因此对于这类算法，OvO是一个优秀的选择，由于在较小的训练集上分别训练多个分类器比在大型数据集上训练少数分类器要快得多。但对于大多数二元分类器，OvA策略还是更好的选择。

4.1 支持向量机二元分类器

sklearn 检测到尝试使用二元分类器进行多分类任务时，会根据情况自动运行ovo或者是ova

from sklearn.svm import SVC
#二元分类器默认使用 OneVsOne 策略进行预测 多分类问题
svm_clf = SVC()
# sklearn内部实际训练了45个二元分类器   采用OneVsOne-clf策略
svm_clf.fit(x_train_lit,y_train_lit)
res = svm_clf.predict([x_train_[0]])
print(res)

# 查看多元分类器对第一个数值的预测分数
digit_scores = svm_clf.decision_function([x_train_[0]])
# 取出分数中的最大值索引
print(np.argmax(digit_scores))  # 5
# 查看分类类别
print(svm_clf.classes_[5])  # 5

强制二元分类器使用 OneVsRest（也称One V All）策略进行预测

    from sklearn.multiclass import OneVsRestClassifier
    ovr_clf = OneVsRestClassifier(SVC())
    ovr_clf.fit(x_train_lit,y_train_lit)
    res = ovr_clf.predict([x_train_[0]])
    print(res)

4.2 SGD 多元分类器

直接使用多分类器时 sklean不需要再次运行策略，因为多分类器可以直接将实例分为多个类

    sgd_clf = SGDClassifier(random_state=42)
    sgd_clf.predict([x_train_[0]])
    sgd_clf.decision_function([x_train_[0]])
    
	# 使用交叉验证评估模型
    cross_val_score(sgd_clf,x_train_lit,y_train_lit,cv=3,scoring='accuracy')

	# 提高准确率 标准化处理
    from sklearn.preprocessing import StandardScaler
    scaler = StandardScaler()
    x_train_scaled = scaler.fit_transform(x_train_lit)
    scores = cross_val_score(sgd_clf, x_train_scaled, y_train_lit, cv=3, scoring='accuracy')
    print(scores)

误差分析查看多分类的混淆矩阵

    y_train_pred = cross_val_predict(sgd_clf,x_train_scaled,y_train_lit,cv=3)
    conf_mx = confusion_matrix(y_train_lit,y_train_pred)

使用 matplotlib中的 matshow()来可视化混淆矩阵

    plt.matshow(conf_mx,cmap=plt.cm.gray)
    plt.show()

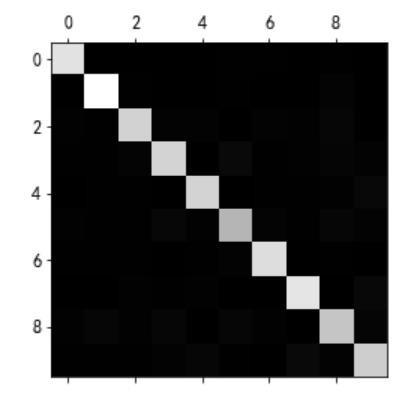
5稍微暗一点，可能意味着数据集中5的图片少，也可能是分类器在5上的执行效果不行。实际上，这二者都属实。
让我们把焦点都放在错误上。
首先，我们需要将混淆矩阵中的每个值都除以相应类别中的图片数，这样比较的是错误率，而不是错误的绝对值==(后者对图片数量较多的类别不公平)==

     # 按行相加，并保持数组原维度的特性, 每个实例有多少张图片
    rows_sum = conf_mx.sum(axis=1,keepdims=True)  
    print(rows_sum)
    # 错误数除以总图片数
    nrow_conf_mx = conf_mx / rows_sum
    print(nrow_conf_mx)

0是黑，255是白，越白的位置说明错误率越高
行表示实际类别，列表示预测的类别，可以看到 8 9 列比较亮，容易其他数字容易被分错为8 9， 8 9 行业比较亮，说明 8 9 容易被错误分为其他数字。此外3 容易被错分为 5，5也容易被错分为4。
分析混淆矩阵，通常可以帮助我们深入了解如何改进分类器。通过上面的图，我们可以花费更多时间来改进8 9的分类，以及修正 3 5 的混淆上。
分析单个错误也可以为分类器提供洞察：它在做什么？为什么失败？但这通常更加困难和耗时。例如，我们来看看数字3和数字5的例子：

cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]

plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()

我们可以看到，虽然有一些数字容易混淆，但大多数，还是比较好分类的，但算法还是会分错。因为SGD模型是一个线性模型，它所做的就是为每一个像素分配一个各个类别的权重，当它看到新的图像时，将加权后的像素强度汇总，从而得到一个分数进行分类。而数字3和5只在一部分像素位上有区别，所以分类器很容易将其搞混。

数字3和5之间的主要区别在于连接顶线和下方弧线中间的小线条的位置。如果我们写的数字3将连续点略往左移，分类器就可能将其分类为5，反之亦然。换言之，这个分类器对图像位移和旋转非常敏感，因此，减少3 5混淆的方法之一是对数字进行预处理，确保他们位于中心位置，并且没有旋转。这也有助于减少其他错误。

5. 多标签分类

到目前位置，每个实例都只有一个输出，但某些情况下，我们需要分类器为每个实例产出多个类别，比如，为照片中的每个人脸附上一个标签。
假设分类器经过训练，已经可以识别三张脸 A B C，那么当看到A和C的合照时，应该输出[1,0,1]，这种输出多个二元标签的分类系统成为多标签分类系统
下面以k近邻算法为例(不是所有的分类器都支持多标签)

    # KNN支持多标签的分类   不是所有的分类器都支持多标签的分类
    y_train_large = (y_train_lit >=7)  # 是否大于7
    y_train_odd = (y_train_lit%2 ==1)  # 是否为奇数
    # np.c_用法见第一章  ctrl+c查找
    y_multilabel = np.c_[y_train_large,y_train_odd]

    knn_clf = KNeighborsClassifier()
    knn_clf.fit(x_train_lit,y_multilabel)

    res = knn_clf.predict([x_train_[0]])
    print(res)  # [[False  True]]  不是大于7的  是奇数

结果正确，x_train_[0]的真实标签是5，显然它小于7，同时是奇数
#[[False True]] 预测正确

评估多标签分类器的方法很多，如何选择正确的度量指标取决于我们的项目。比如方法之一是测量每个标签的F1分数(或者是之前讨论过的任何其他二元分类器指标),然后简单的平均。

# 耗时比较长，可以选择前1000个图片进行测试，节省时间
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3, n_jobs=-1)
f1_score(y_multilabel, y_train_knn_pred, average="macro")

这里假设了所有的标签都是同等重要，但实际的数据可能并不均衡，可以修改average=“weighted”,来给每个标签设置一个等于其自身支持的权重

6. 多输出分类

现在，我们将讨论最后一种分类任务–多输出多分类任务(简称为多输出分类)。简单而言，它是多标签分类的泛化，其标签也可以是多种类别的(比如有两个以上的值)

任务说明:构建一个去除图片中噪声的系统。给它输入一个带噪声的图片，它将(希望)输出一张干净的数字图片，跟其他MNIST图片一样，以像素强度的一个数组作为呈现方式。
需要注意的是：这个分类器的输出时多个标签(一个像素点一个标签),每一个标签有多个值(0-255)。所以这是一个多输出分类器系统的例子。

# 将训练集和测试集的图片上 添加噪声
noise = np.random.randint(0,100,(len(x_train_lit),784))
x_train_nos = x_train_lit + noise
noise = np.random.randint(0, 100, (len(x_test_lit), 784))
x_test_nos = x_test_lit + noise

# 目标值改为干净的，没有噪声的图片
y_train_nos = x_train_lit
y_test_nos = x_test_lit

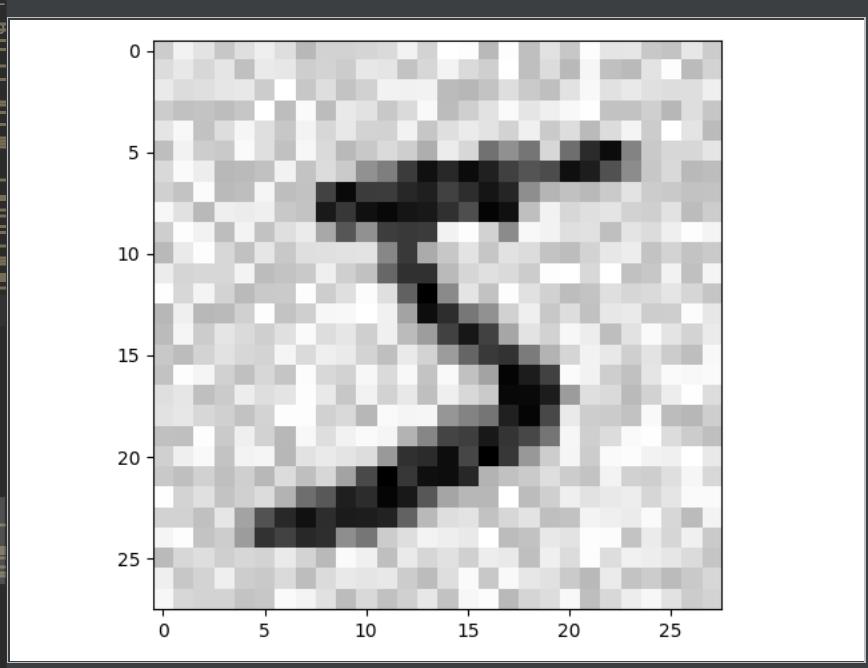
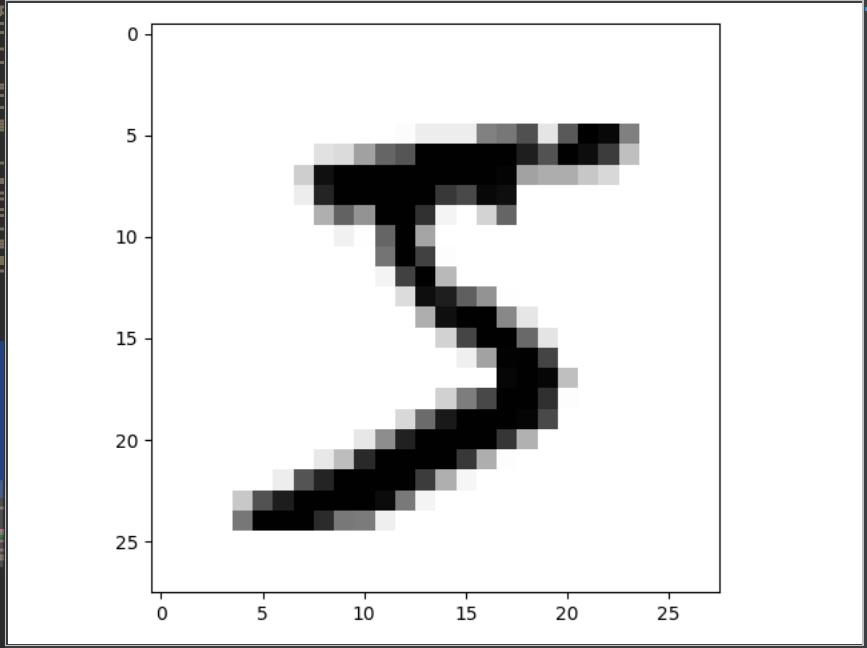
查看原始图片和噪声图片

    x_train_dig = x_train_nos[0].reshape(28,28)
    y_train_dig = y_train_nos[0].reshape(28,28)
    plt.imshow(x_train_dig,cmap = plt.cm.binary)
    plt.show()
    plt.imshow(y_train_dig,cmap = plt.cm.binary)
    plt.show()

噪声图片：

原始图片：

训练模型：

    knn_clf.fit(x_train_nos,y_train_nos)
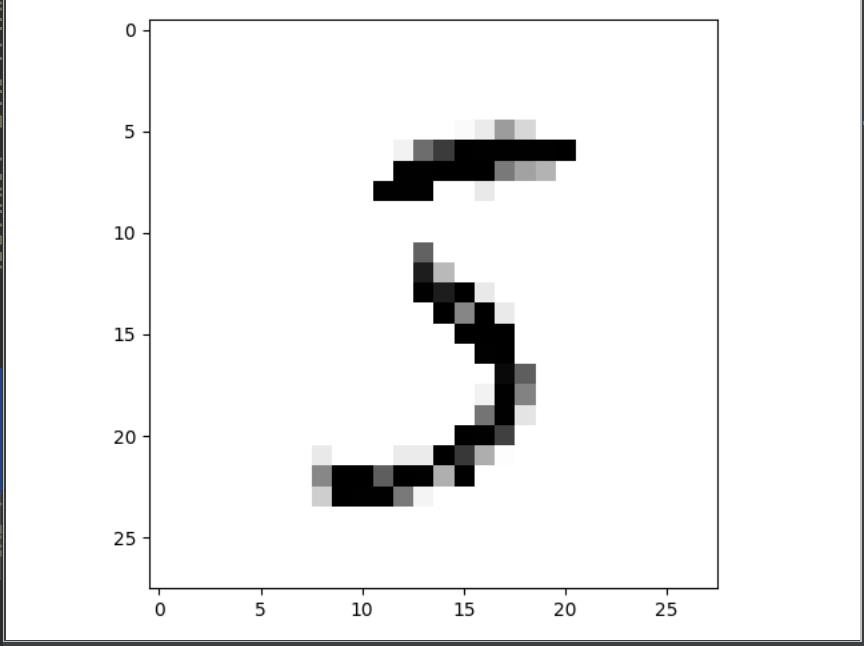
    #  predict测试效果
    clean_digit = knn_clf.predict([x_train_nos[0]])
    # 显示图片
    clean_digit = clean_digit.reshape(28,28)
    plt.imshow(clean_digit,cmap = plt.cm.binary)
    plt.show()

效果：