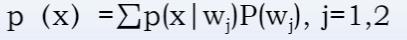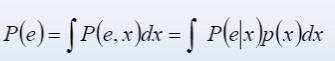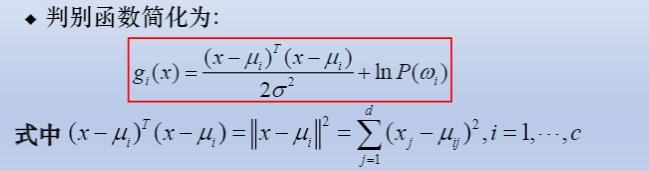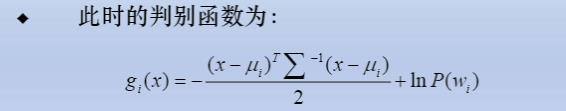MOOC:模式识别——贝叶斯决策理论
Posted 庄园特聘拆椅狂魔
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MOOC:模式识别——贝叶斯决策理论相关的知识,希望对你有一定的参考价值。
1.理解贝叶斯不得不说的基础四概念
先验概率——预先已知的历史概率或统计得出的概率,表示样本属于某种类型的概率
类条件概率——某类型数据集中样本x出现的概率
全概率——全部数据集中样本x出现的概率<=>样本x在各个类别总出现的概率的和
后验概率——样本x属于某个类别的概率
x,样本 wi表示第i个类型
(先验概率)
(类条件概率)
(全概率)
(后验概率)
贝叶斯决策:根据后验概率进行决策,将样本归类于后验概率大的类型,使总体错误率最小
贝叶斯公式:D表示某一样本,wi表示第i类型
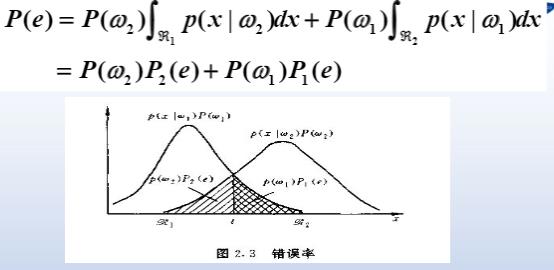
错误率:所有服从同样分布的独立样本上错误的概率的期望
分类错误率:被错分的样本数/样本总数
2.两种贝叶斯决策(最小错误率和最小风险)
贝叶斯决策的目标:使错误率最小,使分类尽可能的正确
1.基于最小错误率的贝叶斯决策
什么叫做最小错误率:即后验概率最大
贝叶斯分类器在最小化分类错误率上是最优的。
最小错误率的物理意义:

2.基于最小风险的贝叶斯决策
什么叫做最小风险:使每种决策下条件风险最小(由决策表给出的损失函数和属于该类的后验概率的乘积和组成),则对所有x做出决策时,其期望风险最小。
关键概念:决策、决策空间、决策函数(通常以表格给出,称决策表,根据决策和状态决定损失)

αi 表示决策,由 αi 和状态 (类型) wi 确定 入(αi,wi)
理解为在最小错误率的概念上,配置决策(权重)的概念,计算属于各个类型的后验概率与某决策下的权重的乘积的和——即该决策下的条件期望损失
决策下的权重(来自决策表)——表示的是该决策下对应各个状态的损失函数(提前会给出)
3.最小错误率和基于最小风险的关系:
最小错误率贝叶斯决策是最小风险贝叶斯决策的特殊情况。
4.其他: 错误率指平均错误率
无特殊说明情况下,贝叶斯决策通常指最小错误率贝叶斯决策
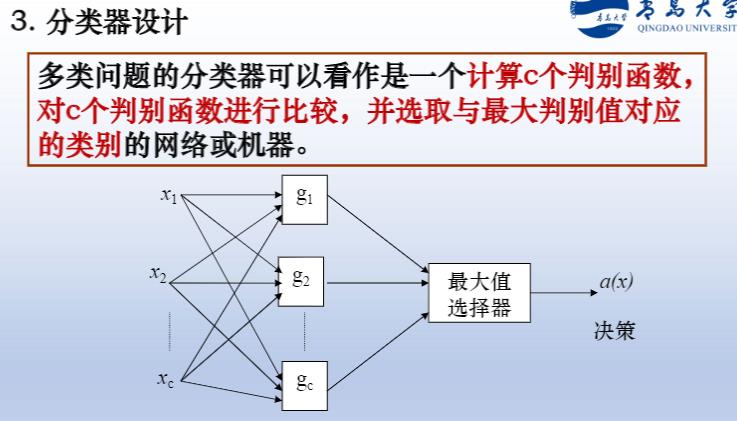
3.贝叶斯分类器
1.什么是贝叶斯分类器:采用贝叶斯分类原理的分类器(选择具有最大后验概率的类作为该样本的类)
2.设计贝叶斯分类器:
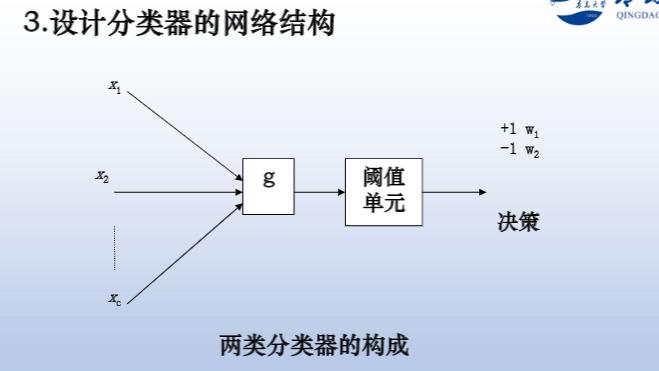
三个步骤:确定判别函数——>写出决策面方程——>设计分类器
两分类问题:

多分类问题:

4.正态分布时的统计决策
正态分布:多数随机变量服从近似服从正态分布,具有良好的数学性质,便于数据分析。
单变量正态分布:
多变量正态分布:
正态分布模型下的最小错误率贝叶斯决策:
第一种情况 第二种情况 第三种情况(最一般的情况) 协方差矩阵 协方差矩阵相等
且是对角阵
类间各特征间相互独立,具有相等的方差
协方差元素为0
协方差矩阵相等
各类均值向量是任意的
协方差矩阵不相等
最一般的情况
几何 各类样本落入以Ui为中心,同样大小的超球体内 相当于各类样本集中于以该类均值为中心同样大小和形状的超椭球内 二类问题判定面为超二次曲面 第一类判别方程:
第二类判别方程:
第三类判别函数:

以上是关于MOOC:模式识别——贝叶斯决策理论的主要内容,如果未能解决你的问题,请参考以下文章