Python数学建模系列:数值逼近
Posted 海轰Pro
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python数学建模系列:数值逼近相关的知识,希望对你有一定的参考价值。
文章目录
前言
Hello!小伙伴!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,有幸拿过一些国奖、省奖…已保研。目前正在学习C++/Linux/Python
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
初学Python 小白阶段
文章仅作为自己的学习笔记 用于知识体系建立以及复习
题不在多 学一题 懂一题
知其然 知其所以然!
往期文章
1. 一维插值
插值:求过已知有限个数据点的近似函数。
插值函数经过样本点,拟合函数一般基于最小二乘法尽量靠近所有样本并穿过。常见差值方法有拉格朗日插值法、分段插值法、样条插值法。

interp1d(x, y) 计算一维插值
1.1 线性插值与样条插值(B-spline)
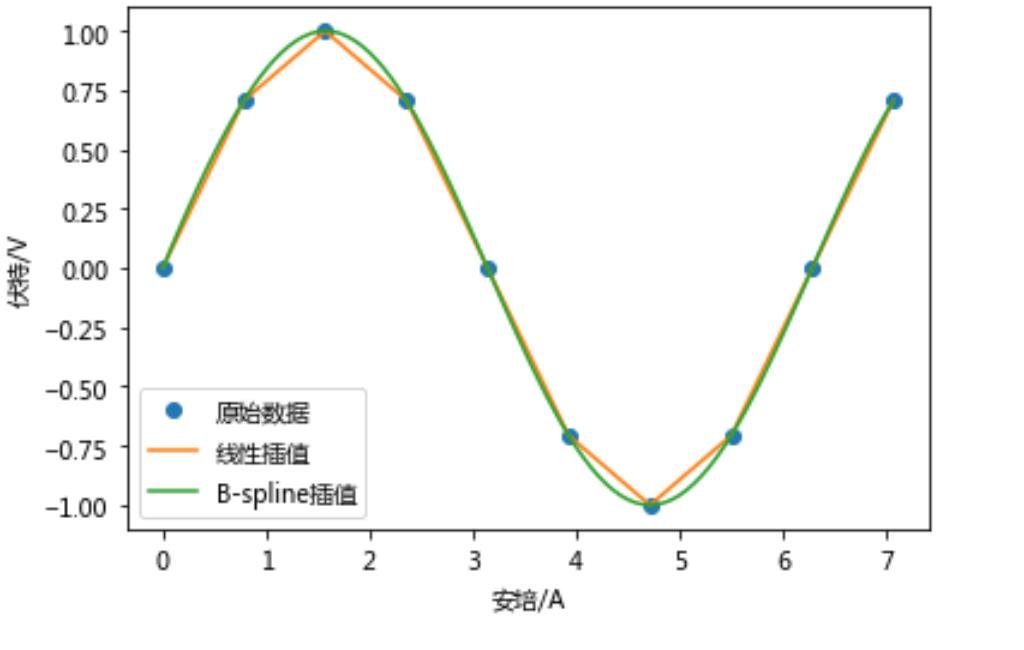
例1:某电学元件的电压数据记录在0~2.25πA范围与电流关系满足正弦函数,分别用线性插值和样条插值方法给出经过数据点的数值逼近函数曲线。
Demo代码
import matplotlib
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
# 引入中文字体
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 初始数据量 0 - 2.25pi 分为10份 均匀分
x = np.linspace(0, 2.25 * np.pi, 10)
y = np.sin(x)
# 得到差值函数 (使用线性插值)
f_linear = interpolate.interp1d(x, y)
# 新数据 0 - 2.25pi 分为100份 均匀分 (线性插值)
x_new = np.linspace(0, 2.25 * np.pi, 100)
y_new = f_linear(x_new)
# 使用B-spline插值
tck = interpolate.splrep(x, y)
y_bspline = interpolate.splev(x_new, tck)
# 可视化
plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f_linear(x_new), label=u"线性插值")
plt.plot(x_new, y_bspline, label=u"B-spline插值")
plt.legend()
plt.show()
输出:
涉及知识点:
- numpy.linspace
- scipy.interpolate.interp1d
- scipy.interpolate.splrep
1.2 高阶样条插值
随着插值节点增多,多项式次数也变高,插值曲线在一些区域出现跳跃,并且越来越偏离原始曲线,称为龙格现象。
例2:某电学元件的电压数据记录在010A范围与电流关系满足正弦函数,分别用05阶样条插值方法给出经过数据点的数值逼近函数曲线。
Demo代码
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 绘制数据点集
plt.figure(figsize=(12, 9))
plt.plot(x, y, 'ro')
# 根据kind创建interp1d对象f、计算插值结果
xnew = np.linspace(0, 10, 101)
# 邻接 0阶 线性 二阶
for kind in ['nearest', 'zero', 'linear', 'quadratic']:
f = interpolate.interp1d(x, y, kind=kind)
ynew = f(xnew)
plt.plot(xnew, ynew, label=str(kind))
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(loc="lower right")
plt.show()
输出:
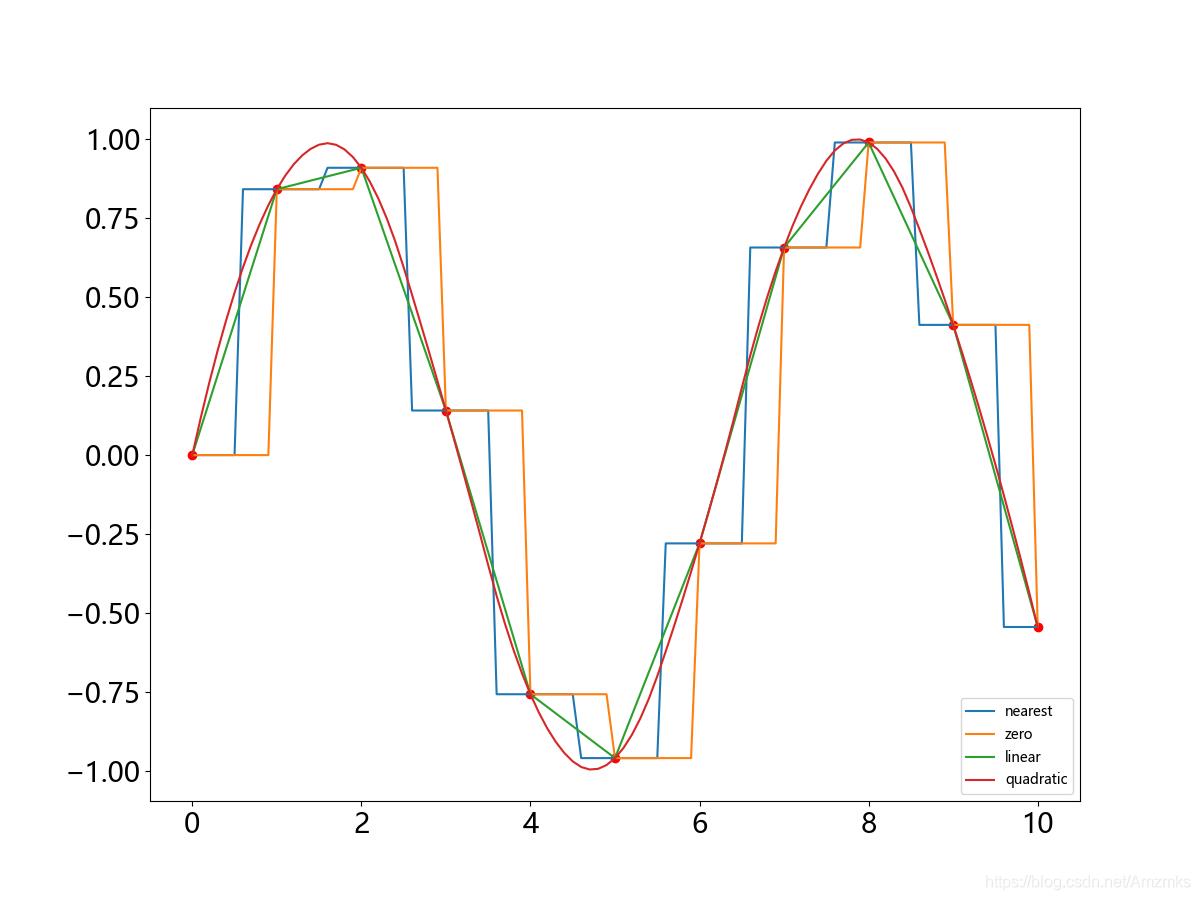
分别对每一种插值方式进行查看
1.当kind = nearest时
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 得插值函数
f = interpolate.interp1d(x, y, kind='nearest')
# 新数据
x_new = np.linspace(0,10,101)
y_new = f(x_new)
# 可视化
plt.plot(x, y, 'o', x_new, y_new, '-')
plt.show()
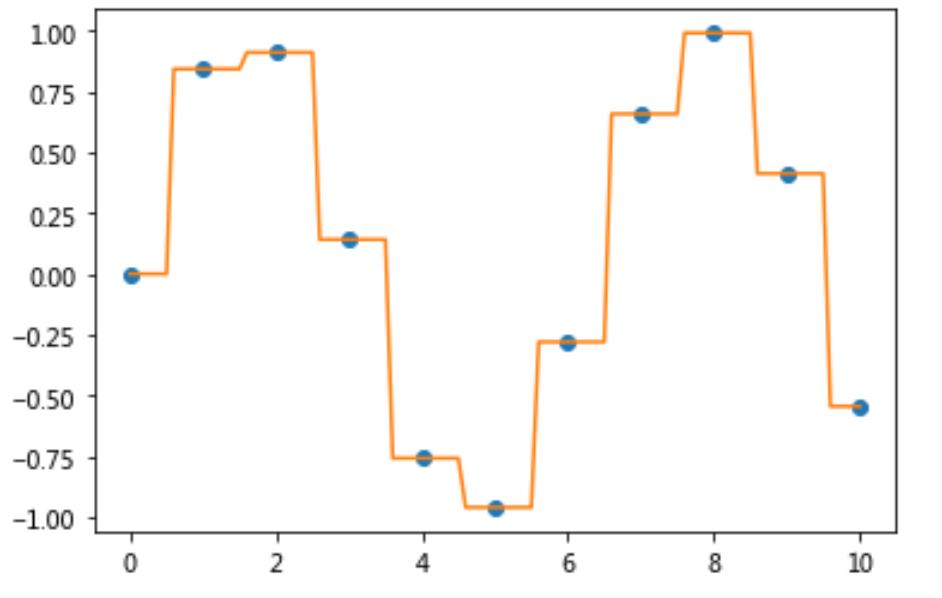
2.当kind = zero时
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 得插值函数
f = interpolate.interp1d(x, y, kind='zero')
# 新数据
x_new = np.linspace(0,10,101)
y_new = f(x_new)
# 可视化
plt.plot(x, y, 'o', x_new, y_new, '-')
plt.show()
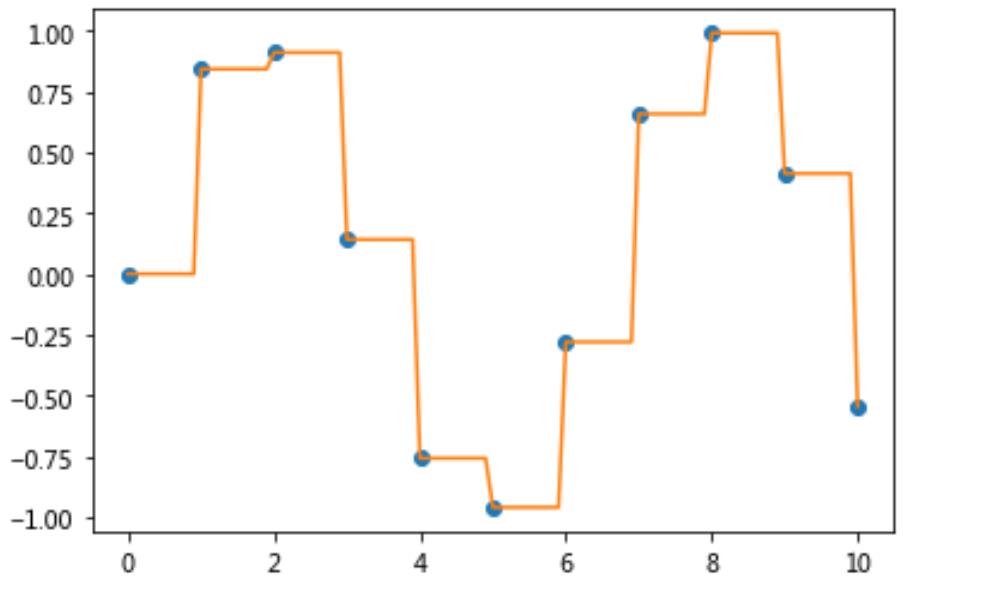
3.当kind = linear时
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 得插值函数
f = interpolate.interp1d(x, y, kind='linear')
# 新数据
x_new = np.linspace(0,10,101)
y_new = f(x_new)
# 可视化
plt.plot(x, y, 'o', x_new, y_new, '-')
plt.show()
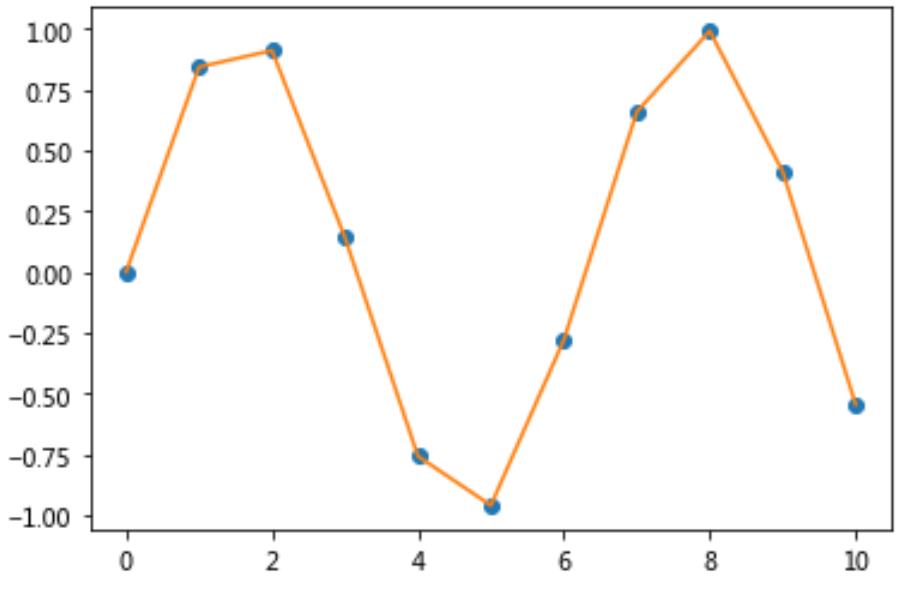
4.当kind = quadratic时
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 得插值函数
f = interpolate.interp1d(x, y, kind='quadratic')
# 新数据
x_new = np.linspace(0,10,101)
y_new = f(x_new)
# 可视化
plt.plot(x, y, 'o', x_new, y_new, '-')
plt.show()
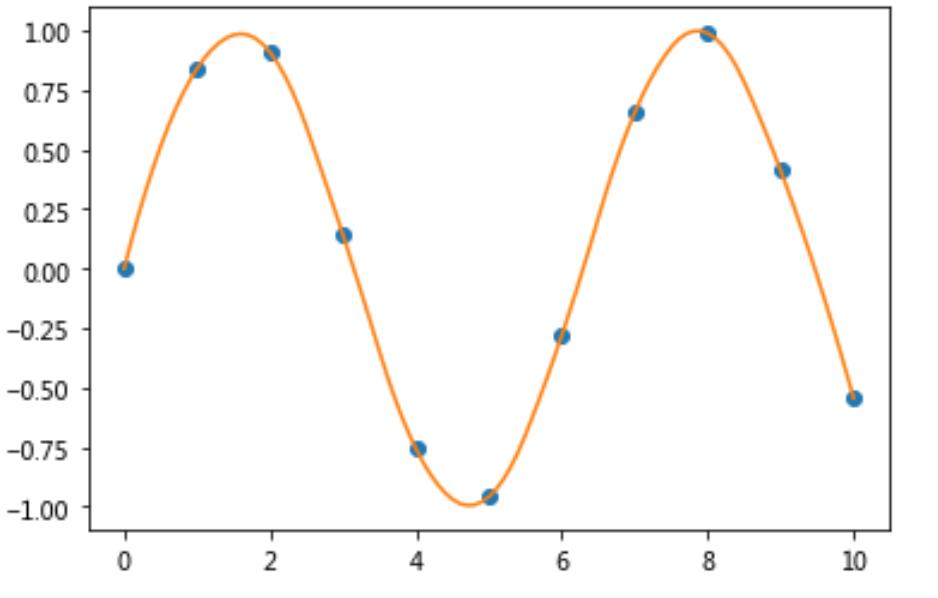
5.当kind = cubic时
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
from scipy import interpolate
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)
# 得插值函数
f = interpolate.interp1d(x, y, kind='cubic')
# 新数据
x_new = np.linspace(0,10,101)
y_new = f(x_new)
# 可视化
plt.plot(x, y, 'o', x_new, y_new, '-')
plt.show()
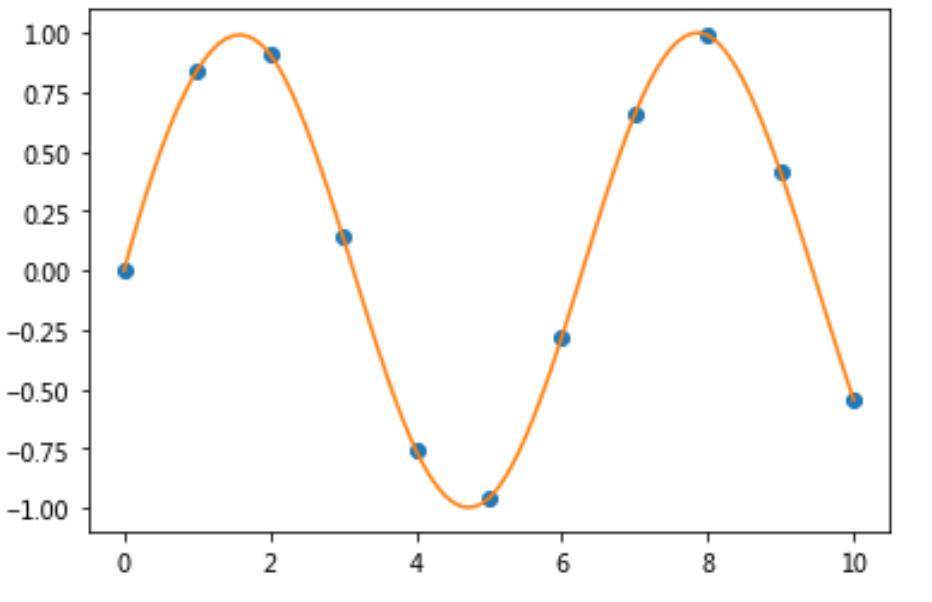
2. 二维插值
interp2d(x, y, z, kind=“’’) 计算二维插值
2.1 图像模糊处理——样条插值
例3:某图像表达式为 z = ( x + y ) e − 5 ∗ ( x 2 + y 2 ) z = (x+y)e^{-5*(x^2 + y^2)} z=(x+y)e−5∗(x2+y2),完成图像的二维插值使其变清晰。
Demo代码
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
def func(x, y):
return (x + y) * np.exp(-5.0 * (x ** 2 + y ** 2))
# X-Y轴分为15*15的网格
# x, y = np.mgrid[-1:1:15j, -1:1:15j]
x = np.linspace(-1, 1, 15)
y = np.linspace(-1, 1, 15)
x, y = np.meshgrid(x, y)
fvals = func(x, y)
# 二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
# 计算100*100网格上插值
xnew = np.linspace(-1, 1, 100)
ynew = np.linspace(-1, 1, 100)
fnew = newfunc(xnew, ynew)
xnew, ynew = np.meshgrid(xnew, ynew)
plt.subplot(121)
# extent x轴和y轴范围
im1 = plt.imshow(fvals, extent=[-1, 1, -1, 1], interpolation="nearest", origin="lower",cmap="Reds")
plt.colorbar(im1)
plt.subplot(122)
im2 = plt.imshow(fnew, extent=[-1, 1, -1, 1], interpolation="nearest", origin="lower",cmap="Reds")
plt.colorbar(im2)
plt.show()
输出:
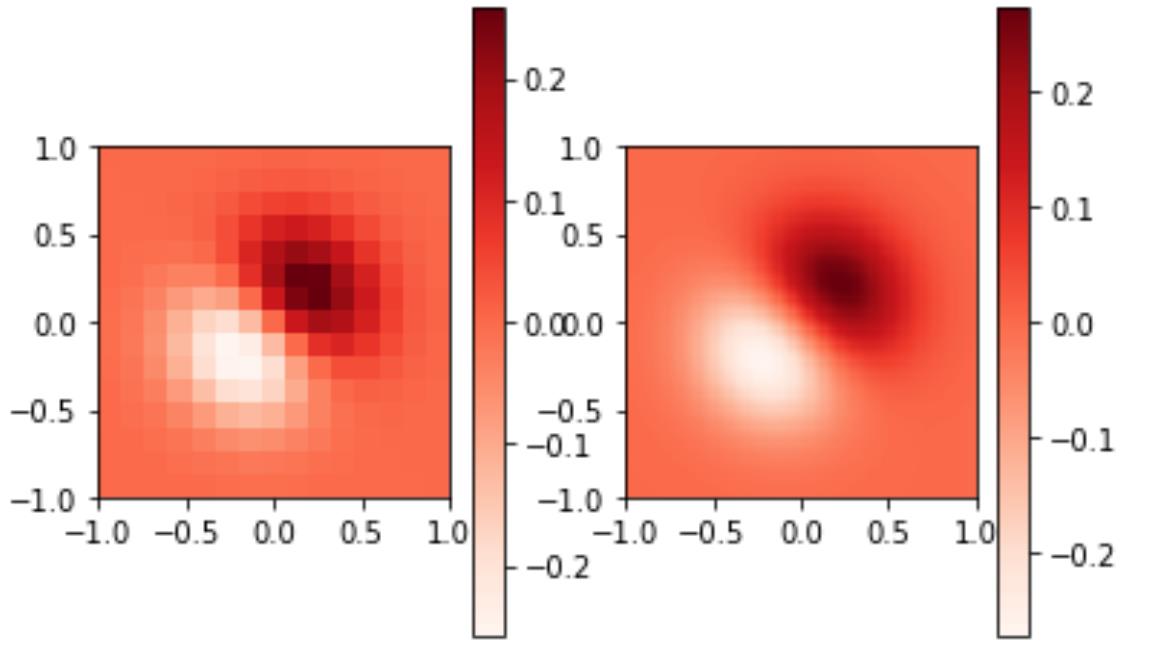
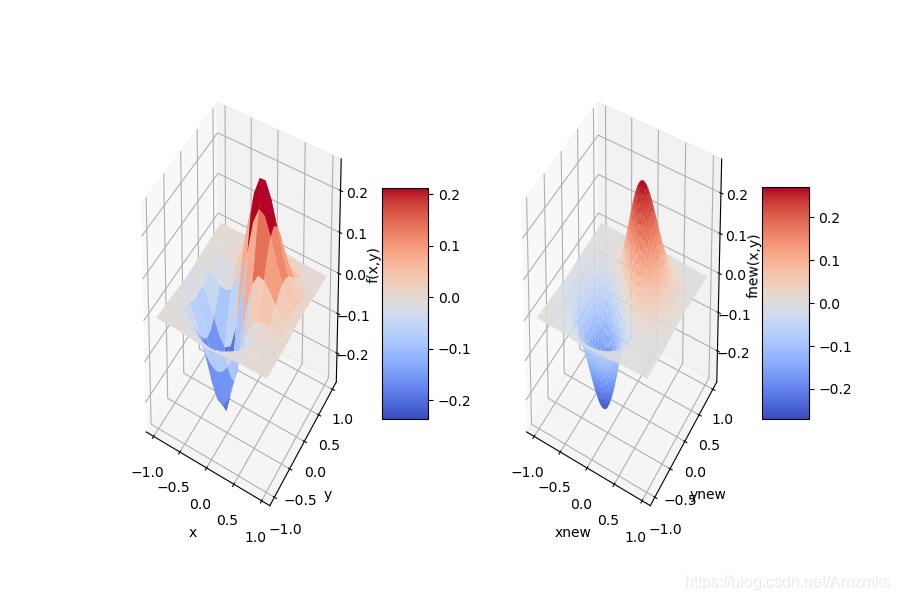
2.2 二维插值的三维图
例4:某图像表达式为
z
=
(
x
+
y
)
e
−
5
∗
(
x
2
+
y
2
)
z = (x+y)e^{-5*(x^2 + y^2)}
z=(x+y)e−5∗(x2+y2),完成三维图像的二维插值可视化。
其实就是在3二维插值基础上 实现了三维图像的绘制
Demo代码
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x, y):
return (x + y) * np.exp(-5.0 * (x ** 2 + y ** 2))
# X-Y轴分为20*20的网格
x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
x, y = np.meshgrid(x, y)
fvals = func(x, y)
# 绘制分图1
fig = plt.figure(figsize=(9, 6))
ax = plt.subplot(1, 2, 1, projection='3d')
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
plt.colorbar(surf, shrink=0.5, aspect=5) # 添加颜色条标注
# 二维插值
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
# 计算100*100网格上插值
xnew = np.linspace(-1, 1, 100)
ynew = np.linspace(-1, 1, 100)
fnew = newfunc(xnew, ynew)
xnew, ynew = np.meshgrid(xnew, ynew)
ax2 = plt.subplot(1, 2, 2, projection='3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm, linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x,y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)
# 标注
plt.show()
输出:
3. 最小二乘拟合
拟合指的是已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函 数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别(最小二乘意义)最小。
如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。表达式也可以是分段函数,这种情况下叫作样条拟合。
从几何意义上讲,拟合是给定了空间中的一些点,找到一个已知形式、未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。
选择参数c使得拟合模型与实际观测值在曲线拟合各点的残差(或离差)ek=yk-f(xk,c)的加权平方和达到最小,此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线,这种方法叫做最小二乘法。
涉及知识点
from scipy.optimize import leastsq
例5:对下列电学元件的电压电流记录结果进行最小二乘拟合,绘制相应曲线。
电流(A)8.19 2.72 6.39 8.71 4.7 2.66 3.78
电压(V)7.01 2.78 6.47 6.71 4.1 4.23 4.05

Demo代码
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
# 引入中文字体
font = {
"family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)
# 设置图字号
plt.figure(figsize=(9, 9))
# 初始数据值
X = np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
Y = np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
# 计算以p为参数的直线与原始数据之间误差
def f(p):
k, b = p
return (Y - (k * X + b))
# leastsq使得f的输出数组的平方和最小,参数初始值k、b设为[1,0]
r = leastsq(f, [1, 0])
# 得到计算出的最优k、b
k, b = r[0]
# 可视化
plt.scatter(X, Y, s=100, alpha=1.0, marker='o', label=u'数据点')
x = np.linspace(0, 10, 1000)
y = k * x + b
ax = plt.gca()
plt.plot(x, y, color='r', linewidth=5, linestyle=":", markersize=20, label=u'拟合曲线')
plt.legend(loc=0, numpoints=1)
leg = plt.gca().get_legend()
ltext = leg.get_texts()
plt.setp(ltext, fontsize以上是关于Python数学建模系列:数值逼近的主要内容,如果未能解决你的问题,请参考以下文章