Python数学建模系列：图论

Posted 2021-09-11 海轰Pro

文章目录

• 前言
• 往期文章
• 1 图论模型 - Dijkstra
• • 样例1
• 2 图论模型-Floyd
• • 样例2
• 3 机场航线设计
• • 0、Airlines.csv数据
  • 1、数据导入、观察变量
  • 2、数据清洗
  • 3、时间信息合并
  • 4、创建图
  • 5、计算航线
• 结语

前言

Hello！小伙伴！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～
 
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖…已保研。目前正在学习C++/Linux/Python
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！
 
初学Python 小白阶段
文章仅作为自己的学习笔记 用于知识体系建立以及复习
题不在多 学一题 懂一题
知其然 知其所以然！

往期文章

Python数学建模系列（一）：规划问题之线性规划

Python数学建模系列（二）：规划问题之整数规划

Python数学建模系列（三）：规划问题之非线性规划

Python数学建模系列（四）：数值逼近

Python数学建模系列（五）：微分方程

Python数学建模系列（六）：蒙特卡洛算法

Python数学建模系列（七）：差分

1 图论模型 - Dijkstra

Dijkstra算法能求一个顶点到另一顶点最短路径。

基础概念

• 无向图： 若图中的每条边都是没有方向的，则称该图为无向图。
• 有向图： 若图中的每条边都是有方向的，则称该图为有向图。
• 混合图： 若图中的部分边是有方向的，而部分边是无方向的，则称该图为混合图。

样例1

如下图所示，我们需要从①点走到⑨点，每条边的红色数 字代表这条边的长度，我们如何找到①到⑨的最短路径呢？

步骤：

1. 将①标记为P，其它标记为T，找出从①出发当前最短的边所到的点，将该点的T改为P
2. 将所有P点找到可以到达的T标记点上最短的边，将到达的点T改为P
3. 重复步骤，指导终点的T变为P

过程展示：圈加数字代表每个顶点，()内数字代表当前行走的距离

1.①(0)
2.①②(1)
3.①②⑤(3)
4.①②⑤(3)      ①④(3)
5.①②⑤⑦(5)     ①④(3)
6.①②⑤⑦⑥(6)     ①④(3)
7.①②⑤⑦⑥(6)     ①②⑤③(6)     ①④(3)
8.①②⑤⑦⑥(6)     ①②⑤③④(7)     ①④(3)
9.①②⑤⑦⑥⑧(8)     ①②⑤③④(7)     ①④(3)
10.①②⑤⑦⑥⑧(8)     ①②⑤⑦⑨(8)     ①②⑤③④(7)     ①④(3)

所以最短的路径是 ① ② ⑤ ⑦ ⑨， 长度为8

带权邻接矩阵： 带权邻接矩阵是表示顶点相邻关系的矩阵，例如上面那个图的带权邻接矩阵如下

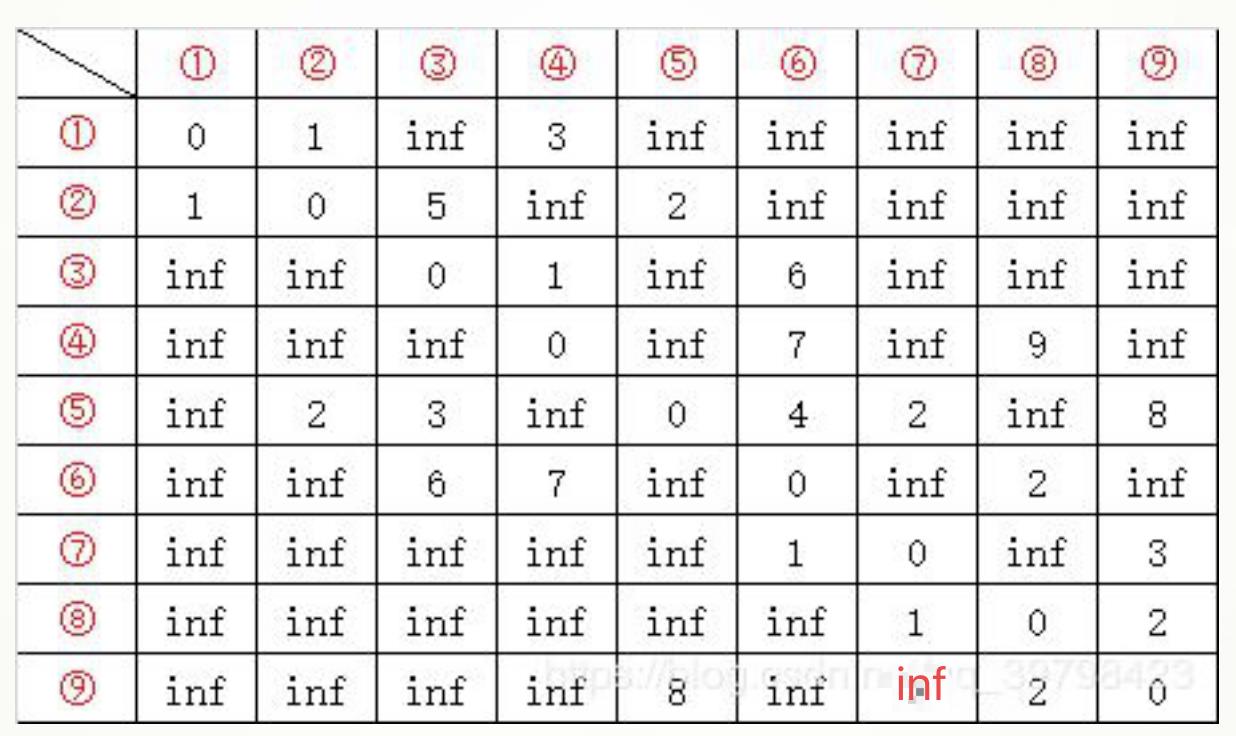
注意：原PPT中有错误， 点9 -> 点7 应该为inf （上图已经修改）

每个点和自己的距离为0（主对角线上元素都是零）

在图上相邻两个点的如果是连通的，距离就是矩阵的值，无向 的关于主对角线对称；有向的只有可以过去的路有数值

无法连通的距离就是无穷，记为inf

Demo代码

# 运行环境：Vs Code
# PPT中代码有点错误 已经修改～ 
# 以下代码经测试 可行
from collections import defaultdict 
from heapq import * 
inf = 99999 # 不连通值 
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
             [1, 0, 5, inf, 2, inf, inf, inf, inf],
             [inf, inf, 0, 1, inf, 6, inf, inf, inf],
             [inf, inf, inf, 0, inf, 7, inf, 9, inf],
             [inf, 2, 3, inf, 0, 4, 2, inf, 8],
             [inf, inf, 6, 7, inf, 0, inf, 2, inf],
             [inf, inf, inf, inf, inf, 1, 0, inf, 3],
             [inf, inf, inf, inf, inf, inf, 1, 0, 2], 
             [inf, inf, inf, inf, 8, inf, inf, 2, 0]]
m_n = len(mtx_graph)#带权连接矩阵的阶数 
edges = [] #保存连通的两个点之间的距离(点A、点B、距离) 
for i in range(m_n): 
    for j in range(m_n): 
        if i!=j and mtx_graph[i][j]!=inf: 
            edges.append((i,j,mtx_graph[i][j])) 

def dijkstra(edges, from_node, to_node): 
    go_path = [] 
    to_node = to_node-1 
    g = defaultdict(list) 
    for l,r,c in edges:
        # l:点A r:点B c:距离 
        # 字典： 点A -> (距离，点B)
        g[l].append((c,r)) 
    q, seen = [(0, from_node-1, ())], set()
    while q: 
        (cost, v1, path) = heappop(q)#堆弹出当前路径最小成本 
        if v1 not in seen: 
            seen.add(v1) 
            path = (v1, path) 
            if v1 == to_node: 
                break 
            for c, v2 in g.get(v1, ()): 
                if v2 not in seen: 
                    heappush(q, (cost+c, v2, path)) 
                
    if v1!=to_node:   #无法到达 
        return float('inf'), []
    if len(path)>0: 
        left=path[0] 
        go_path.append(left) 
        right=path[1] 
        while len(right)>0: 
            left=right[0] 
            go_path.append(left) 
            right=right[1] 
            
        go_path.reverse() #逆序变换 
        for i in range(len(go_path)): #标号加1 
            go_path[i]=go_path[i]+1 
    return cost, go_path 
leght, path = dijkstra(edges, 1, 9) 
print('最短距离为：'+str(leght)) 
print('前进路径为：'+str(path))

运行结果

最短距离为：8
前进路径为：[1, 2, 5, 7, 9]

2 图论模型-Floyd

Floyd算法通过动态规划解决任意两点间的最短路径（多源最短路径）的问题，可以正确处理负权的最短路径问题

关键原理：

$$d[i][j]=min(d[i][k]+d[k][j])(1<=k<=n)$$
枚举中间点k，找到最小的$d[i][k]+d[k][j]$，作为$d[i][j]$的最小值

关键结论：

假设i和j之间的最短路径上的结点集里(不包含i，j)，编号最大的一个是x.那么在外循环k = x时，$d[i][j]$ 肯定得到了最小值.

强归纳法 :

设i到x中间编号最大的是x1，x到j中间编号最大的是x2.由于x是i到j中间编号最大的，那么显然$x_1<x,x_2<x$

根据结论，$k=x_1$时候$d[i][x]$已经取得最小值，$k=x_2$时候$d[x][j]$已经取得最
小值

那么$k=x$时，$d[i][x]$和$d[x][j]$已经都取得最小值.

因此$k=x$时，执行$d[i][j]=min(d[i][j],d[i][k]+d[k][j])得d[i][j]$

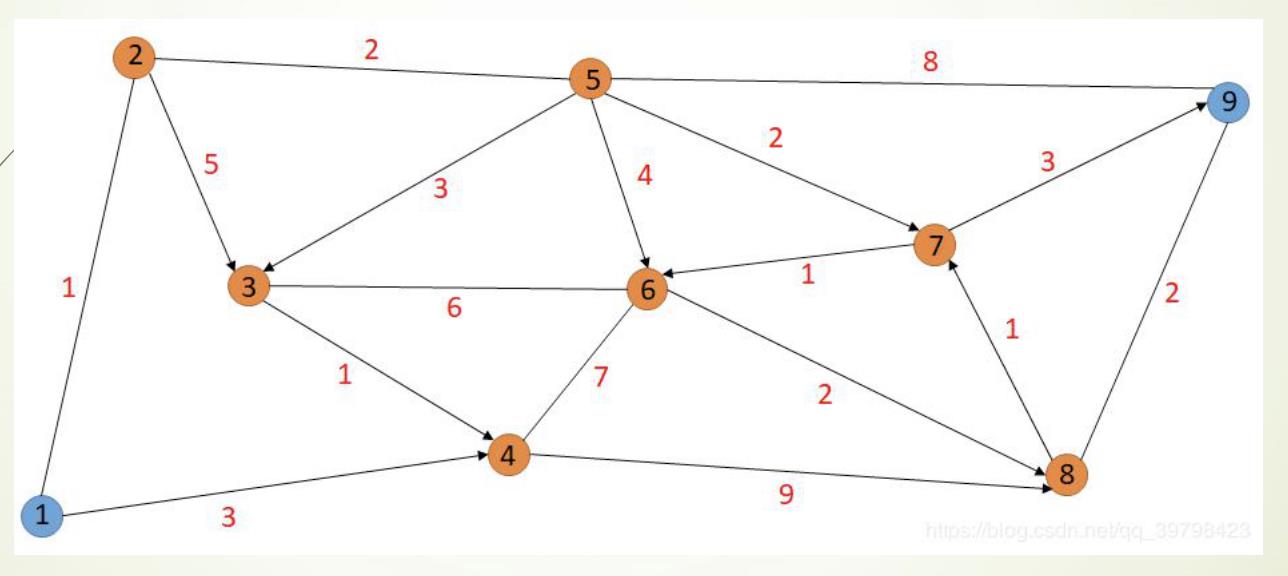
样例2

与样例1相似，只是这次我们求出从每一个点到其他点的最短距离和路径，每条边的红色数字代表这条边的长度。

Demo代码

from collections import defaultdict 
from heapq import * 
import numpy as np
inf = 99999 # 不连通值 
mtx_graph = [[0, 1, inf, 3, inf, inf, inf, inf, inf],
             [1, 0, 5, inf, 2, inf, inf, inf, inf],
             [inf, inf, 0, 1, inf, 6, inf, inf, inf],
             [inf, inf, inf, 0, inf, 7, inf, 9, inf],
             [inf, 2, 3, inf, 0, 4, 2, inf, 8],
             [inf, inf, 6, 7, inf, 0, inf, 2, inf],
             [inf, inf, inf, inf, inf, 1, 0, inf, 3],
             [inf, inf, inf, inf, inf, inf, 1, 0, 2], 
             [inf, inf, inf, inf, 8, inf, inf, 2, 0]]
def Floyd(graph): 
    N=len(graph) 
    A=np.array(graph)
    path=np.zeros((N,N)) 
    for i in range(0,N): 
        for j in range(0,N): 
            if A[i][j]!=inf: 
                path[i][j]=j 
    for k in range(0,N): 
        for i in range(0,N): 
            for j in range(0,N):
                # 原PPT这一句代码有错 写成了 A[i][j]+A[k][j]<A[i][j]
                # 正确应该是：A[i][k]+A[k][j]<A[i][j]
                if A[i][k]+A[k][j]<A[i][j]: 
                    A[i][j]=A[i][k]+A[k][j] 
                    path[i][j]=path[i][k]
    for i in range(0,N): 
        for j in range(0,N): 
            path[i][j]=path[i][j]+1 
    print('距离 = ') 
    print(A) 
    print('路径 = ') 
    print(path) 

Floyd(mtx_graph)

运行结果

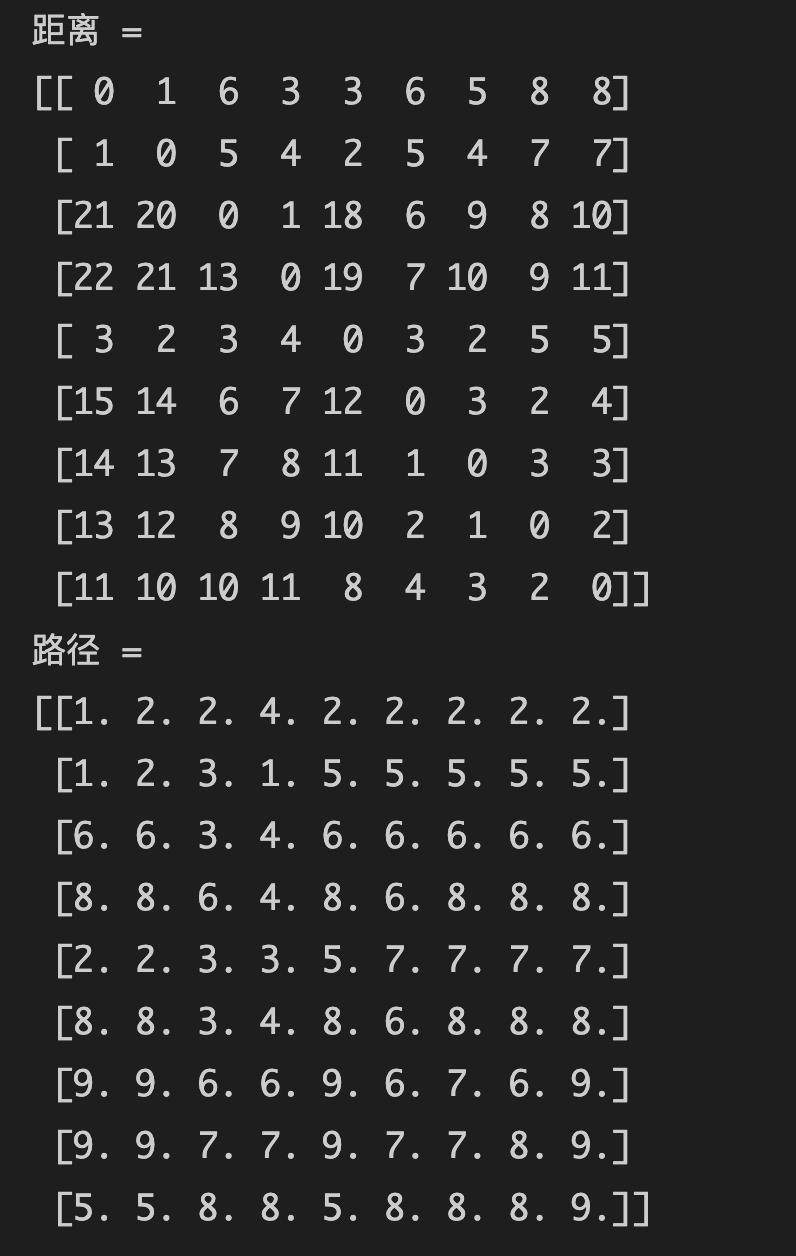
注意：原PPT 结果中 最后一行又错 应该是 5. 5. 8. 8. 5. 8. 8. 8. 9. PPT中是： 5. 5. 7. 7. 5. 7. 7. 8. 9. 因为在最初的 mtx_graph 设置就错了：点9到点7 应该是inf 而不是 3

结论：

• 从点1 到 点9 的距离为8（结果中“距离”矩阵中第一行第九列数值）
• 路径为【1 - 2 - 5 - 7 - 9】

怎么看路径呢？

• 从最后结果中查看”路径“矩阵
• 点1 到 点9 首先看第一行第九列 数值为2
• 这是中间位置2，再看第二行第九列，数值为5
• 再看第五行第九列，数值为7
• 再看第七行第九列，数值为9
• 得到最终路径【1 - 2 - 5 - 7 - 9】

3 机场航线设计

数据集来自航空业，有一些关于航线的基本信息。有某段旅程的起始点和目的地。还有一些列表示每段旅程的到达和起飞时间。这个数据集非常适合作为图进行分析。想象一下通过航线（边）连接的几个城市（节点）。

如果你是航空公司，你可以问如下几个问题：

• 从A到B的最短途径是什么？分别从距离和时间角度考虑。
• 有没有办法从C到D？
• 哪些机场的交通最繁忙？
• 哪个机场位于大多数其他机场“之间”？这样它就可以变成当地的一个中转站。

0、Airlines.csv数据

1、数据导入、观察变量

import numpy as np 
import pandas as pd 
data = pd.read_csv('../Profile/Airlines.csv') 
data.shape #数据大小 

# (100, 16) 100行16列

运行结果

查看各个变量的类型

data.dtypes # 各变量的类型

运行结果

2、数据清洗

#将sched_dep_time转换为'std'—预定的出发时间 
data['std'] = data.sched_dep_time.astype(str).str.replace('(\\d{2}$)', '') + ':' + data.sched_dep_time.astype(str).str.extract('(\\d{2}$)', expand=False) + ':00'
 
#将sched_arr_time转换为“sta”—预定到达时间
data['sta'] = data.sched_arr_time.astype(str).str.replace('(\\d{2}$)', '') + ':' + data.sched_arr_time.astype(str).str.extract('(\\d{2}$)', expand=False) + ':00'
 
#将dep_time转换为'atd' -实际出发时间 
data['atd'] = data.dep_time.fillna(0).astype(np.以上是关于Python数学建模系列：图论的主要内容，如果未能解决你的问题，请参考以下文章
 
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：匹配的概念
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：匹配的概念
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：树及其性质
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：树及其性质
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：生成树算法
 机器学习｜数学基础Mathematics for Machine Learning系列之图论：生成树算法