精选算法题——枚举符合要求的算术表达式(DFS回溯法)

Posted 2021-09-11 翟天保Steven

题目描述：

约定按照自然优先级，并且不使用括号，在数字'0'~'9'之间加入加号'+'或乘号'*’，构成合法的算术表达式。

对于任一给定的整数S，枚举出所有值为S的上述类型表达式。

示例：

图1 示例

解题思路：

本题适合用回溯法和深度优先遍历DFS解决。具体思路如下：

1. 首先，罗列出所有符合要求的数字，放置在Inum容器中，比如123、12、234等等，前提是要小于整数S；
2. 定义辅助函数——Calculation，使其读入一个string类型的算术表达式，比如1+3+5+6*7，能返回结果；
3. 定义辅助函数——findnum，用来寻找下个符合要求的数所在的位置，比如1+2+3，后面可以放置4，也可以放置45，也可以放置456,；
4. 求解函数DFS：DFS用flag来标记要用乘法还是加法，从Inum中挨个读取，因为0和9一定是单数，所以第一个读取的应该是0，拿到0后存放在str中，str用来标记当前已经有多少个数字在表达式中了，比如01234，那接下来就要找5开头的数字；字符串s用来存放表达式；开始深度优先遍历，id是当前位置，从id+1进入循环，用Calculation判断当前表达式结果是否大于S，好处是可以使遍历过程快速收敛，达到提速目的；若当前表达式符合要求，用findnum函数寻找Inum中符合要求的数字并存储其下标，基于该下标继续调用DFS，进入递归，一层层下去相当于深入到最里面的节点，即深度优先；当DFS执行到最后一个数9，用Calculation计算是否等于S，存储符合要求的表达式，返回上级节点；回归上级节点后，别忘了将str和s重置，比如1+2+3+4不合格了，那就继续执行1+2+3+45，s存放的应该是1+2+3+；当DFS执行完，结果就全出来了，因为每次运算到9后，后面还跟了一次加法和一次乘法，即9+和9*，这样就导致每次结果都存放了两次，因而输出result的时候需要间隔输出。

测试代码：

#include <iostream>
#include <string>
#include <vector>
#include <time.h>

using namespace std;

vector<int> num = { 0,1,2,3,4,5,6,7,8,9 };
vector<string> result;
int number;

// 计算string表示的算术表达式
int Calculation(string& exp, int start, int end)
{
	int am = 0, md = 0;
	// 标记最后出现的加减乘除号位置（不在括号内）
	for (int i = start; i < end; ++i)
	{
		if (exp[i] == '+')
			am = i;
		if (exp[i] == '*')
			md = i;
	}
	// 若有加减号，则将符号前面的内容和后面的内容相加或减
	if (am > start) {
		return Calculation(exp, start, am) + Calculation(exp, am + 1, end);
	}
	// 若有乘除号，则将符号前面的内容和后面的内容相乘或者除
	else if (md > start)
	{
		return Calculation(exp, start, md) * Calculation(exp, md + 1, end);			
	}
	// 若没有加减乘除，也没有内置括号，说明这部分内容是数字
	else
		return stoi(exp.substr(start, end - start));
}

// 寻找下个数在Inum中可能出现的位置
bool findnum(string str,vector<int> &Inum,int &id)
{
	// fin是最后一个字符
	char fin = str[str.size() - 1];
	// 确定下个数的位置
	for (int i = id; i < Inum.size(); ++i)
	{
		string num = to_string(Inum[i]);
		if (num[0] == fin+1)
		{
			id = i;
			return true;
		}
		// 最后一个数字如果是9，说明结束了，不用再计算了
		else if(fin=='9'){
			return false;
		}
	}
	return false;
}

// 回溯法求解
bool DFS(string &str, vector<int>&Inum, int id,string s,bool flag)
{
	str += to_string(Inum[id]);
	if (flag)
	{
		s += to_string(Inum[id]) + "+";
	}
	else {
		s += to_string(Inum[id]) + "*";
	}
	string tstr = str;
	string ts = s;
	// 深度优先遍历
	for (int i = id + 1; i < Inum.size(); ++i)
	{
		// 若某个节点已经大于number，则直接跳过，使计算过程收敛，达到提速目的
		if (Calculation(s, 0, int(s.size() - 1)) < number)
		{
			if (findnum(str, Inum, i))
			{
				DFS(str, Inum, i, s, true);
				DFS(str, Inum, i, s, false);
			}
			else
				break;
			// 回归当前节点
			str = tstr;
			s = ts;
		}
	}
	// 若有结果且有9，说明算术表达式合理且成立
	if (Calculation(s,0,int(s.size() - 1))==number&& str.find('9')!= string::npos)
	{
		result.push_back(s.substr(0,s.size()-1));
		return true;
	}
	return false;
}

int main()
{
	while (cin >> number)
	{
		// Inum存放所有可能出现的数字
		vector<int> Inum = { 0 };
		for (int i = 1; i < 10; ++i)
		{
			int temp = num[i];
			Inum.push_back(temp);
			int k = 10;
			for (int j = i + 1; j < 10; ++j)
			{
				temp = temp * 10 + num[j];
				if (temp > number)
				{
					break;
				}
				Inum.push_back(temp);
			}
		}
		string snum;
		string s;
		// 计算
		clock_t start, end;
		start = clock();
		DFS(snum, Inum, 0, s, true);
		DFS(snum, Inum, 0, s, false);
		end = clock();
		cout << "time:" << (end - start) / CLOCKS_PER_SEC << endl;
		// 输出结果
		if (result.size() != 0)
		{
			for (auto i = 0; i < result.size(); i=i+2)
			{
				cout << result[i] << endl;
			}
		}
		else {
			cout << "no result!" << endl;
		}
		result.clear();
	}
}

测试结果：

图2 结果

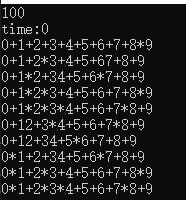
       如果代码有什么需要改进的或者有什么bug，欢迎评论留言，我会及时更正以免误导他人~

       如果文章帮助到你了，可以点个赞让我知道，我会很快乐~加油！