2021-08-25:给定数组father大小为N,表示一共有N个节点,father[i] = j 表示点i的父亲是点j, father表示的树一定是一棵树而不是森林,queries是二维数组,大小为
Posted 福大大架构师每日一题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2021-08-25:给定数组father大小为N,表示一共有N个节点,father[i] = j 表示点i的父亲是点j, father表示的树一定是一棵树而不是森林,queries是二维数组,大小为相关的知识,希望对你有一定的参考价值。
2021-08-25:给定数组father大小为N,表示一共有N个节点,father[i] = j 表示点i的父亲是点j, father表示的树一定是一棵树而不是森林,queries是二维数组,大小为M*2,每一个长度为2的数组都表示一条查询,[4,9], 表示想查询4和9之间的最低公共祖先…,[3,7], 表示想查询3和7之间的最低公共祖先…,tree和queries里面的所有值,都一定在0~N-1之间。返回一个数组ans,大小为M,ans[i]表示第i条查询的答案。
福大大 答案2021-08-25:
树链剖分。
代码用golang编写。代码如下:
package main
import "fmt"
func main() {
father := []int{2, 3, 3, 3, 2, 1}
queries := [][]int{
[]int{2, 0},
[]int{0, 4},
[]int{4, 5},
[]int{1, 0},
[]int{2, 2},
}
ret := query3(father, queries)
fmt.Println(ret)
}
// 在线查询最优解 -> 树链剖分
// 空间复杂度O(N), 支持在线查询,单次查询时间复杂度O(logN)
// 如果有M次查询,时间复杂度O(N + M * logN)
func query3(father []int, queries [][]int) []int {
tc := NewTreeChain(father)
M := len(queries)
ans := make([]int, M)
for i := 0; i < M; i++ {
// x y ?
// x x x
if queries[i][0] == queries[i][1] {
ans[i] = queries[i][0]
} else {
ans[i] = tc.lca(queries[i][0], queries[i][1])
}
}
return ans
}
type TreeChain struct {
n int
h int
tree [][]int
fa []int
dep []int
son []int
siz []int
top []int
}
func NewTreeChain(father []int) *TreeChain {
ans := &TreeChain{}
ans.initTree(father)
ans.dfs1(ans.h, 0)
ans.dfs2(ans.h, ans.h)
return ans
}
func (this *TreeChain) initTree(father []int) {
this.n = len(father) + 1
this.tree = make([][]int, this.n)
this.fa = make([]int, this.n)
this.dep = make([]int, this.n)
this.son = make([]int, this.n)
this.siz = make([]int, this.n)
this.top = make([]int, this.n)
this.n--
cnum := make([]int, this.n)
for i := 0; i < this.n; i++ {
if father[i] == i {
this.h = i + 1
} else {
cnum[father[i]]++
}
}
this.tree[0] = make([]int, 0)
for i := 0; i < this.n; i++ {
this.tree[i+1] = make([]int, cnum[i])
}
for i := 0; i < this.n; i++ {
if i+1 != this.h {
cnum[father[i]]--
this.tree[father[i]+1][cnum[father[i]]] = i + 1
}
}
}
func (this *TreeChain) dfs1(u int, f int) {
this.fa[u] = f
this.dep[u] = this.dep[f] + 1
this.siz[u] = 1
maxSize := -1
for _, v := range this.tree[u] {
this.dfs1(v, u)
this.siz[u] += this.siz[v]
if this.siz[v] > maxSize {
maxSize = this.siz[v]
this.son[u] = v
}
}
}
func (this *TreeChain) dfs2(u int, t int) {
this.top[u] = t
if this.son[u] != 0 {
this.dfs2(this.son[u], t)
for _, v := range this.tree[u] {
if v != this.son[u] {
this.dfs2(v, v)
}
}
}
}
func (this *TreeChain) lca(a int, b int) int {
a++
b++
for this.top[a] != this.top[b] {
if this.dep[this.top[a]] > this.dep[this.top[b]] {
a = this.fa[this.top[a]]
} else {
b = this.fa[this.top[b]]
}
}
return twoSelectOne(this.dep[a] < this.dep[b], a, b) - 1
}
func twoSelectOne(c bool, a int, b int) int {
if c {
return a
} else {
return b
}
}
执行结果如下:
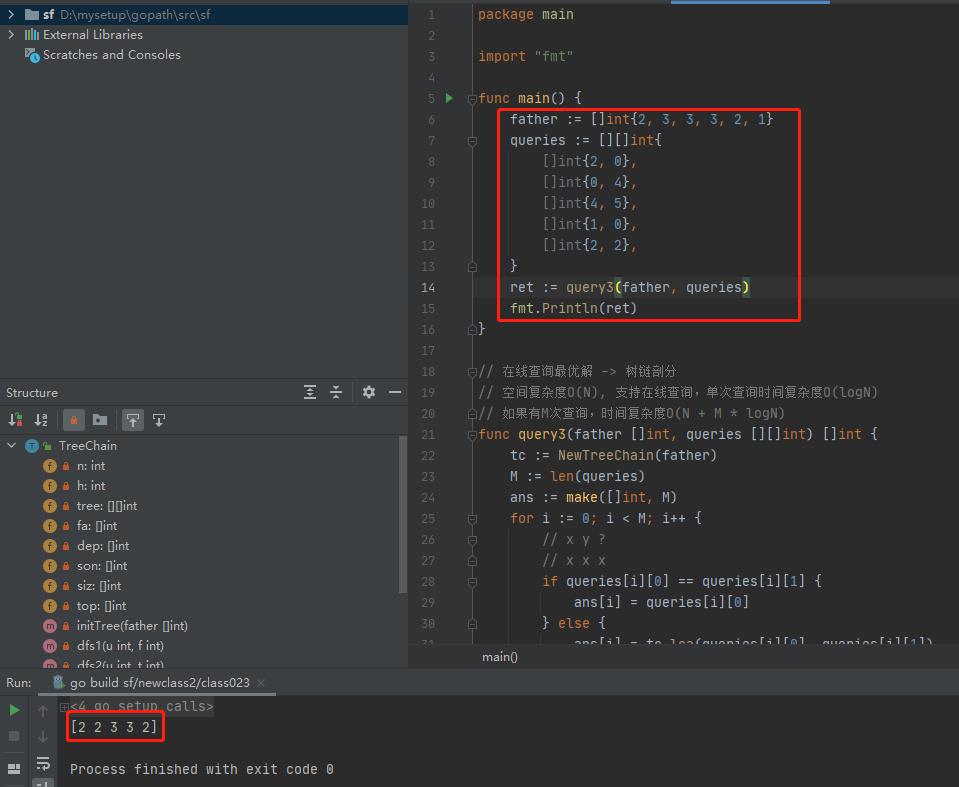
以上是关于2021-08-25:给定数组father大小为N,表示一共有N个节点,father[i] = j 表示点i的父亲是点j, father表示的树一定是一棵树而不是森林,queries是二维数组,大小为的主要内容,如果未能解决你的问题,请参考以下文章