MPC车辆轨迹跟踪----理论推导
Posted QWQ_DIODA
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MPC车辆轨迹跟踪----理论推导相关的知识,希望对你有一定的参考价值。
MPC控制简介
众所周知,控制算法中,PID的应用占据了90%,而另外10%就是这次的主角MPC控制算法。
MPC控制算法全称模型预测控制,它相对比PID有着多输入,多输出以及更加平稳的特点。并且最重要的是,MPC可以针对非线性的系统进行控制。
由于其平稳的和非线性问题有着较强处理能力的特点,其在自动驾驶领域异常流行。
MPC全称:模型预测控制
- 模型:即简单运动学模型,一般需要转化为线性的,离散的
状态空间方程作为基本模型 - 预测:根据模型预测未来数个时间段内(离散的)的状态
- 控制:根据预测内容进行二次优化与处理,得出合适控制量。
简单流程(个人简单理解,若有误请指出)
车辆运动学模型
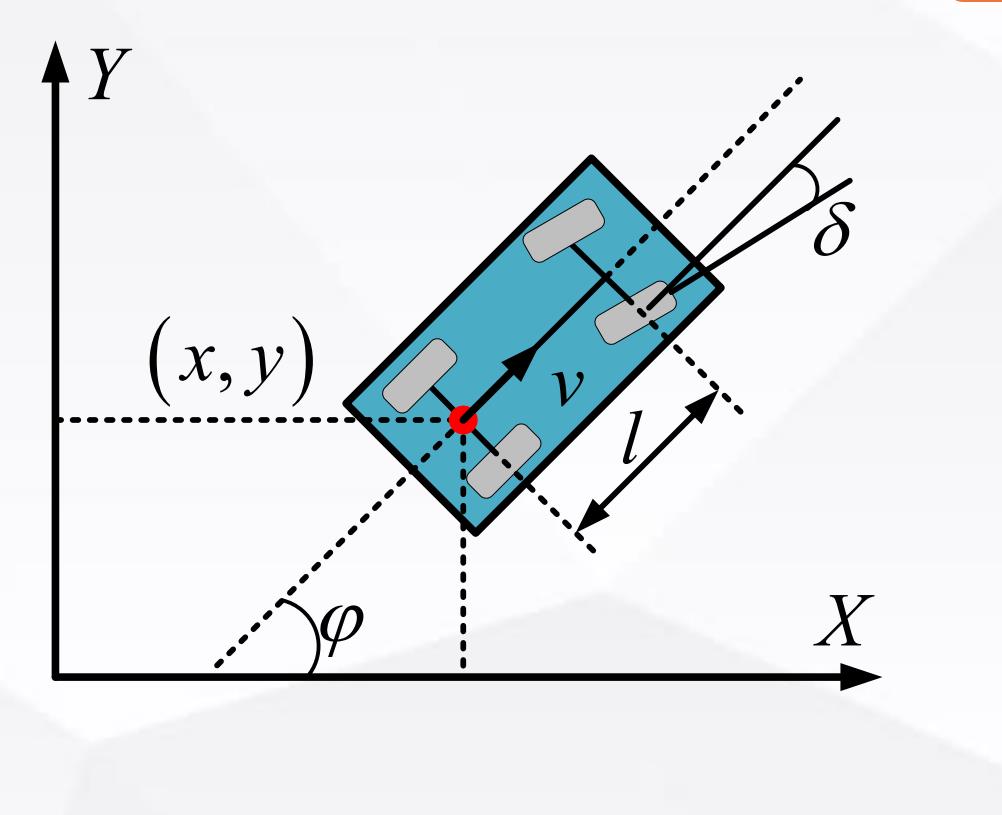
公式为
x ′ = v ∗ cos ( φ ) . y ′ = v ∗ sin ( φ ) . x ′ = v ∗ tan ( δ ) l . x'=v*\\cos(φ).\\\\ y'=v*\\sin(φ).\\\\ x'=\\cfrac{v*\\tan(\\delta)}{l}. x′=v∗cos(φ).y′=v∗sin(φ).x′=lv∗tan(δ).
由于MPC的模型需要、状态空间方程、线性的、离散的表达
因此第一步就是使其成为状态空间方程
完整的表示一个车的状态,我们需要用到他的坐标和角度也就是[x,y,φ]
车辆是一个二自由度模型。控制量分别是:后轮的速度v,前轮的转角δ.
于此,可以确定 以上是关于MPC车辆轨迹跟踪----理论推导的主要内容,如果未能解决你的问题,请参考以下文章
状
态
量
X
=
[
x
y
φ
]
状态量\\Large X =\\large \\begin{bmatrix} x \\\\ y \\\\ φ \\end{bmatrix}
状态量X=⎣⎢⎡xyφ⎦⎥⎤
控
制
量
U
=
[
v
δ
]
控制量\\Large U =\\large \\begin{bmatrix} v \\\\ δ \\end{bmatrix}
控制量U=[vδ]
状
态
空
间
方
程
X
˙
=
f
(
X
,
U
)
状态空间方程\\\\ \\Large \\text{\\.{X}}=\\large f(\\Large X,U)
状态空间方程X˙=f(X,U)
后对状态空间方程进行一阶泰勒展开(线性化)
首先设置参考点(通常为规划好的路径中的参考点)
参
考
点
Xr
˙
=
f
(
X
r
,
U
r
)
参考点\\Large \\text{\\.{Xr}}=\\large f(\\Large Xr,Ur)
参考点Xr˙=f(Xr,Ur)
泰
勒
展
开
:
X
˙
=
f
(
X
r
,
U
r
)
+
δ
f
(
X
,
U
)
δ
X
∗
(
X
−
X
r
)
+
δ
f
(
X
,
U
)
δ
U
∗
(
U
−
U
r
)
.
泰勒展开:\\\\ \\Large \\text{\\.{X}}=\\large f(\\Large Xr,Ur) \\large+ \\cfrac{\\large \\delta f(\\Large X,U)}{\\large \\delta \\Large X}*\\Large(X-Xr)\\large + \\cfrac{\\large \\delta f(\\Large X,U)}{\\large \\delta \\Large U}*\\Large(U-Ur).
泰勒展开:X˙=f(Xr,Ur)+δXδf(X,U)∗(X−Xr)+δUδf(X,U)∗(U−Ur).
由于仍存在无法求得的f(Xr,Ur),因此我们转换策略,改为状态误差量
泰
勒
展
开
:
X
˜
˙
=
X
˙
−
X
˙
r
=
δ
f
(
X
,
U
)
δ
X
∗
(
X
−
X
r
)
+
δ
f
(
X
,
U
)
δ
U
∗
(
U
−
U
r
)
.
泰勒展开:\\\\ \\Large \\text{\\.{\\text{\\~{X}}}}=\\Large \\text{\\.X}-\\text{\\.Xr}=\\large \\cfrac{\\large \\delta f(\\Large X,U)}{\\large \\delta \\Large X}*\\Large(X-Xr)\\large + \\cfrac{\\large \\delta f(\\Large X,U)}{\\large \\delta \\Large U}*\\Large(U-Ur).
泰勒展开:X˜˙=X˙−X˙r=δXδf(X,U)∗(X−Xr)+δUδf(X,U)∗(U−Ur).
X
˜
=
X
−
X
r
U
˜
=
U
−
U
r
\\Large \\text{\\~{X}} = X - Xr\\\\ \\Large \\text{\\~{U}} = U - Ur
X˜