剑指 Offer 11. 旋转数组的最小数字

Posted 2021-09-11 炫云云

剑指 Offer 11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1

示例 2：

输入：[2,2,2,0,1]
输出：0

二分查找

寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 $nums[x]$ ，称 $x$为 旋转点 。

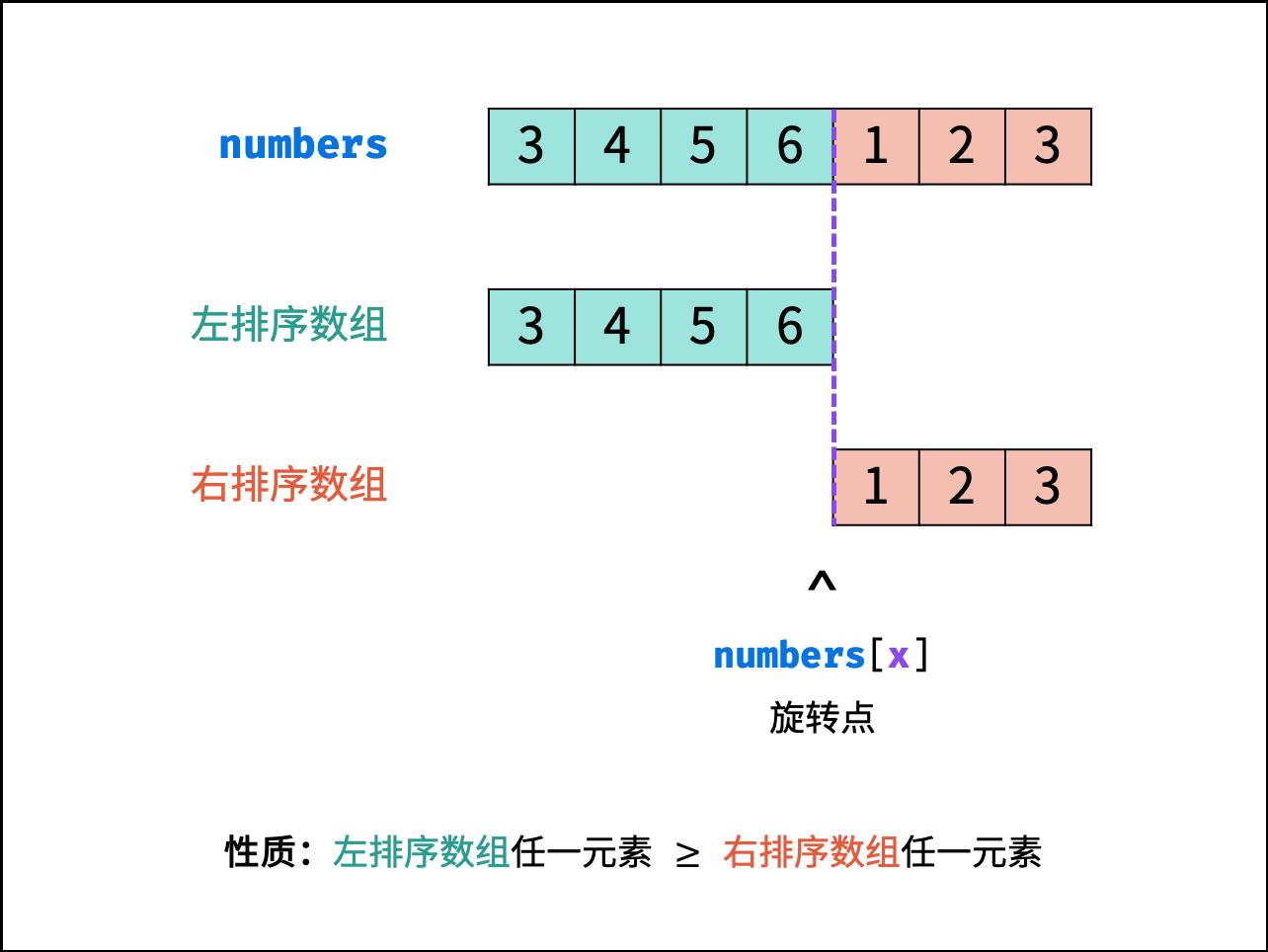
1. 初始化： 声明 $i,j$双指针分别指向 nums 数组左右两端；
   循环二分： 设 $m=(i+j)/2$为每次二分的中点（ “/” 代表向下取整除法，因此恒有 $i\le m<j$ ），可分为以下三种情况：

2. 当 $nums[m]>nums[j]$ 时： $m$一定在 左排序数组 中，即旋转点 $x$一定在 $[m+1,j]$​闭区间内，因此执行 $i=m+1$；

3. 当 $nums[m]<nums[j]$​： $m$​ 一定在 右排序数组 中，即旋转点 $x$ 一定在$[i,m]$闭区间内，因此执行 $j=m$；

4. 当 $nums[m]=nums[j]$时： 无法判断 $m$​ 在哪个排序数组中，即无法判断旋转点 $x$ 在 $[i,m]$还是 $[m+1,j]$区间中。

   代表着 m 可能等于 i 指针的值，或者 j 指针的值，我们这时候只能让 j 指针递减，来一个一个找最小值了。
   解决方案： 执行 $j=j-1$ 缩小判断范围。 返回值： 当 $i=j$ 时跳出二分循环，并返回 旋转点的值 $nums[i]$即可

class Solution(object):
    def minArray(self, numbers):
        """
        :type numbers: List[int]
        :rtype: int
        """
        i, j = 0, len(numbers) - 1
        while i < j:
            #每次二分的中点
            m = i+(j-i)//2
            #旋转点 x在 [m + 1, j]闭区间内
            if numbers[m] > numbers[j]:
                i = m+1
            #旋转点x在[i, m]闭区间内
            elif numbers[m] < numbers[j]:
                j = m
            else:
                #无法判断旋转点 x 在 [i, m]还是 [m + 1, j]区间中
                j -=1
        return numbers[i]

            
if __name__=='__main__':
    s=Solution()
    print(s.minArray([1,3,4,5,0,1,1,1,1,1,1,1,1,1]))#0

0

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)