19推荐系统11FM与深度学习模型的结合
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了19推荐系统11FM与深度学习模型的结合相关的知识,希望对你有一定的参考价值。
一个典型的CTR流程如下图所示:
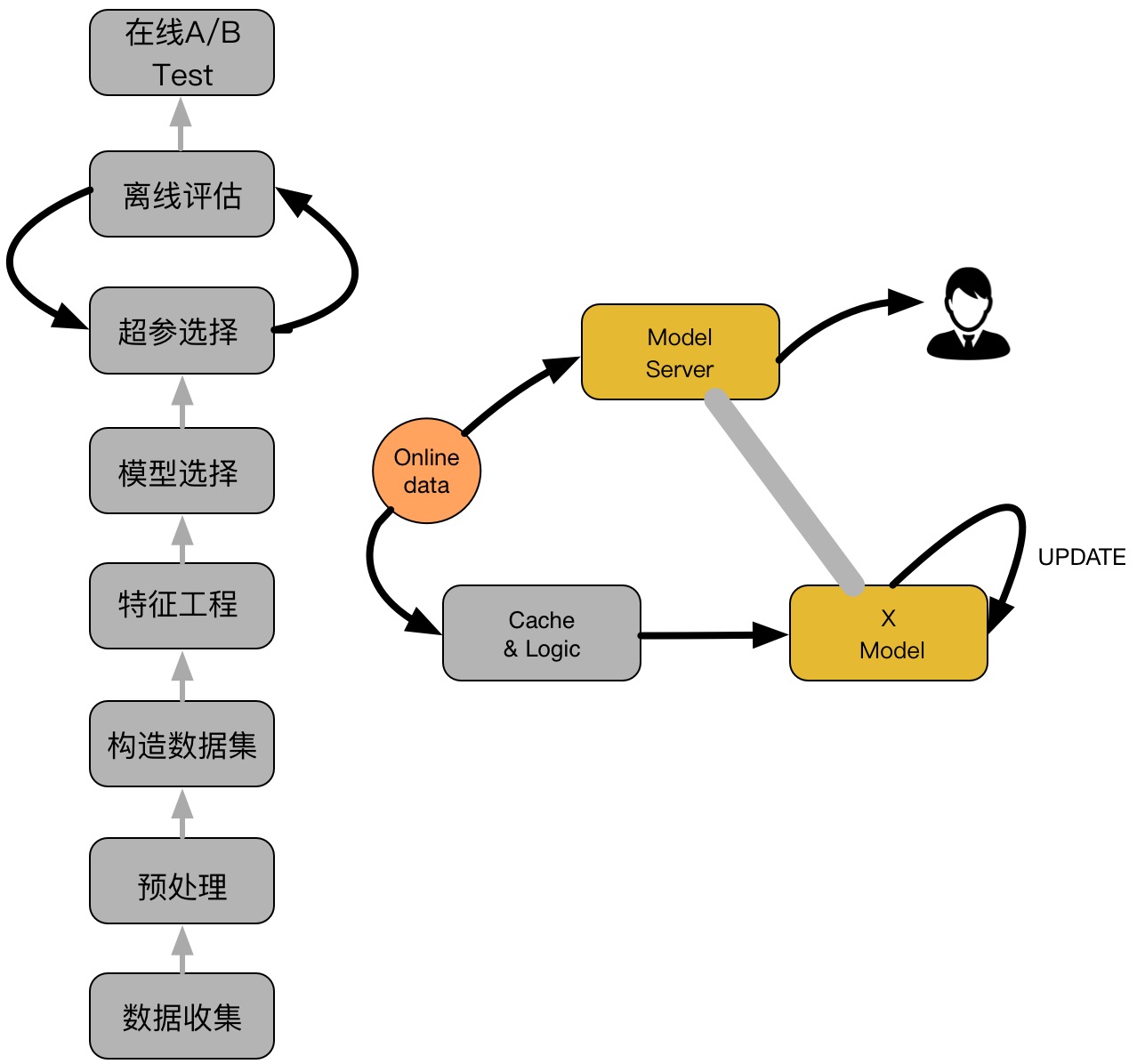
如上图,主要包括两大部分:离线部分、在线部分,其中离线部分目标主要是训练出可用模型,而在线部分则考虑模型上线后,性能可能随时间而出现下降,弱出现这种情况,可选择使用Online-Learning来在线更新模型:
离线部分:
-
数据收集:主要收集和业务相关的数据,通常会有专门的同事在app位置进行埋点,拿到业务数据;
-
预处理:对埋点拿到的业务数据进行去脏去重;
-
构造数据集:经过预处理的业务数据,构造数据集,在切分训练、测试、验证集时应该合理根据业务逻辑来进行切分;
-
特征工程:对原始数据进行基本的特征处理,包括去除相关性大的特征,离散变量one-hot,连续特征离散化等等;
-
模型选择:选择合理的机器学习模型来完成相应工作,原则是先从简入深,先找到baseline,然后逐步优化;
-
超参选择:利用gridsearch、randomsearch或者hyperopt来进行超参选择,选择在离线数据集中性能最好的超参组合;
-
在线A/B Test:选择优化过后的模型和原先模型(如baseline)进行A/B Test,若性能有提升则替换原先模型;
在线部分
- Cache & Logic:设定简单过滤规则,过滤异常数据;
- 模型更新:当Cache &Logic收集到合适大小数据时,对模型进pretrain+finetuning,若在测试集上比原始模型性能高,则更新model server的模型参数;
- Model Server:接受数据请求,返回预测结果;
1、前言
预测用户回应(user response),例如CTR、CVR(转化率)在网页搜索、个性化推荐、在在线广告起着至关重要的作用;广告预测CTR,都依赖于预测是否特定的用户认为这个广告是相关的,给出用户在特定的场景中点击的概率。
不同于图像和音频领域,网页空间的输入特征通常是离散和类别型的,并且依赖性也基本未知;原来要预测用户响应:线性模型(欠拟合)或手工设计高阶交互特征(计算量大);线性模型简单,有效,但是性能偏差,应为无法学习到特征之间的相互关系。非线性模型可以通过特征间的组合提高模型的能力。
通过DNN来自动学习有效的类别特征交互模式,为了使DNN有效工作,利用三个特征转换方法:FM(factorisation machines)、RBM(限制波尔兹曼机)、DAE(降噪自编码器)。
上一节详细介绍了FM模型族的演化过程。在进人深度学习时代后, FM的演化过程并没有停止,本节将介绍的FNN、DeepFM 及NFM模型,使用不同的方式应用或改进了FM模型,并融合进深度学习模型中,持续发挥着其在特征组合上的优势。
2、 FNN——用 FM的隐向量完成Embedding层初始化
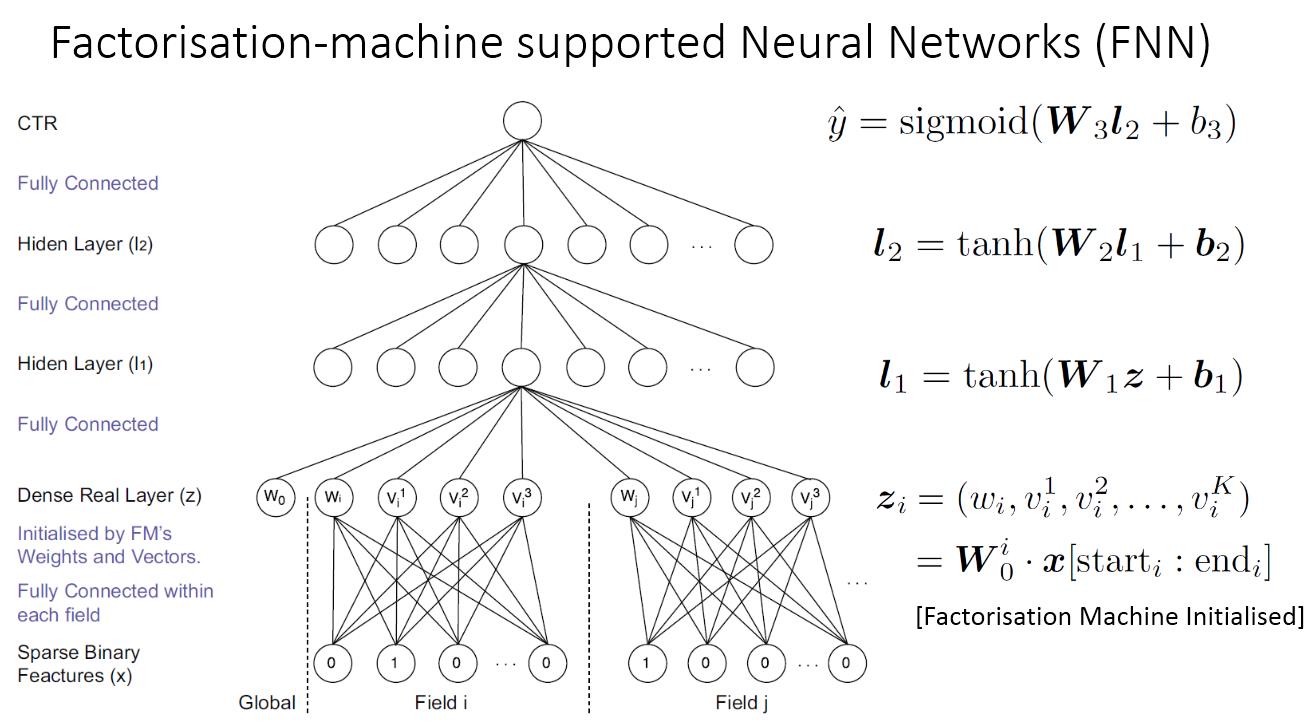
FNN 由伦敦大学学院的研究人员于2016年提出,其模型的结构(如图1所示)初步看是一个类似Deep Crossing 模型的经典深度神经网络,从稀疏输入向量到稠密向量的转换过程也是经典的Embedding 层的结构。那么,FNN 模型到底在哪里与FM模型进行了结合呢?
图
1
:
F
N
N
模
型
的
结
构
图
图1:FNN模型的结构图
图1:FNN模型的结构图
问题的关键还在于Embedding层的改进。在神经网络的参数初始化过程中,往往采用随机初始化这种不包含任何先验信息的初始化方法。由于Embedding层的输入极端稀疏化,导致Embedding层的收敛速度非常级慢。再加上Embedding层的参数数量往往占整个神经网络参数数量的大半以上,因此模型的收敛速度行往受限于Embedding层。
基础知识——为什么Embedding层的收敛速度往往很慢?
在深度学习网络中, Embedding层的作用是将稀疏输入向量转换成稠密向量,但Embedding层的存在往往会拖慢整个神经网络的收敛速度,原因有两个:
- Embedding层的参数数量巨大。这里可以做一个简单的计算。假设输入层的维度是100,000, Embedding 层输出维度是32,上层再加5层32维的全连接层,最后输出层维度是10, 那么输入层到Embedding 层的参数数量是32 x 100,000= 3,200,000,其余所有层的参数总数是(32x32)x4+32x10=4416。那么,Embedding层的权重总数占比是3,200,000 / (3,200,000 + 4416) = 99.86%。也就是说,Embedding层的权重占了整个网络权重的绝大部分。那么,训练过程可想而知,大部分的训练时间和计算开销都被Embedding层占据。
- 由于输人向量过于稀疏,在随机梯度下降的过程中,只有与非零特征相连的Embedding层权重会被更新(请参照随机梯度下降的参数更新公式理,解),这进一步降低了Embedding 层的收敛速度。
针对Embedding层收敛速度的难题,FNN模型的解决思路是用FM模型训练好的各特征隐向量初始化Embedding层的参数,相当于在初始化神经网络参数时,已经引入了有价值的先验信息。也就是说,神经网络训练的起点更接近目标最优点,自然加速了整个神经网络的收敛过程。
这里再回顾一下FM的数学形式,如(式1)所示。
y
F
M
(
x
)
:
=
sigmoid
(
w
0
+
∑
i
=
1
N
w
i
x
i
+
∑
i
=
1
N
∑
j
=
i
+
1
N
⟨
v
i
,
v
j
⟩
x
i
x
j
)
(1)
y_{\\mathrm{FM}}(x):=\\operatorname{sigmoid}\\left(w_{0}+\\sum_{i=1}^{N} w_{i} x_{i}+\\sum_{i=1}^{N} \\sum_{j=i+1}^{N}\\left\\langle v_{i}, v_{j}\\right\\rangle x_{i} x_{j}\\right) \\tag{1}
yFM(x):=sigmoid(w0+i=1∑Nwixi+i=1∑Nj=i+1∑N⟨vi,vj⟩xixj)(1)
其中的参数主要包括常数偏置
w
0
w_{0}
w0, 一阶参数部分
w
i
w_{i}
wi 和二阶隐向量部分
v
i
v_{i}
vi。
图1中,模型底层先用FM对经过one-hot binary编码的输入数据进行embedding,把稀疏的二进制特征向量映射到 dense real 层,之后再把dense real 层作为输入变量进行建模,这种做法成功避免了高维二进制输入数据的计算复杂度。
由于输入层是dense real 层, 每个field是one-hot类型, 所以:
z i = W 0 i ⋅ x [ start i : e n d i ] = ( w i , v i 1 , v i 2 , … , v i K ) (2) \\boldsymbol{z}_{i}=\\boldsymbol{W}_{0}^{i} \\cdot \\boldsymbol{x}\\left[\\operatorname{start}_{i}:\\right. end \\left._{i}\\right]=\\left(w_{i}, v_{i}^{1}, v_{i}^{2}, \\ldots, v_{i}^{K}\\right) \\tag{2} zi=W0i⋅x[starti:endi]=(wi,vi1,vi2,…,viK)(2)
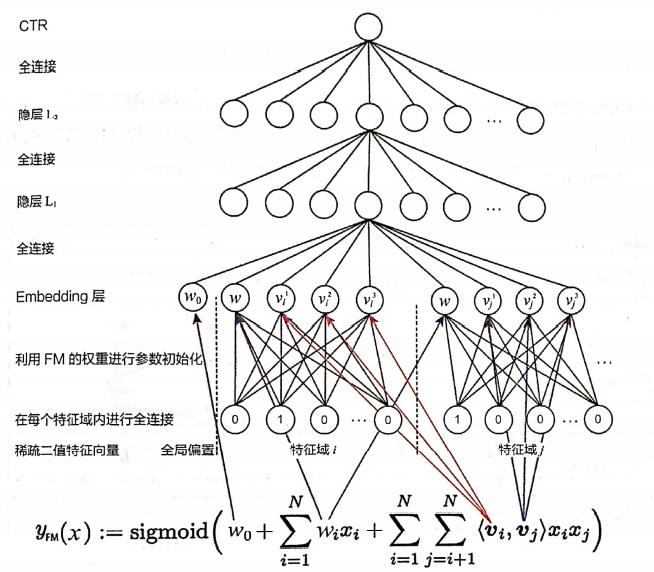
下面用图示的方法显示FM各参数和FNN中Embedding层各参数的对应关系(如图2所示)。
图
2
:
利
用
F
M
初
始
化
E
m
b
e
d
d
i
n
g
层
的
过
程
图2:利用FM初始化Embedding层的过程
图2:利用FM初始化Embedding层的过程
通过这种方法,上面的神经网络可以从FM的表示中更加有效的学习。可以学到更加多的潜在的数据间的模式,能够得到更好的效果。
FM层和其他的层进行初始化之后,再通过监督学习的方法进行finetune,使用交叉熵的损失函数:
L ( y , y ^ ) = − y log y ^ − ( 1 − y ) log ( 1 − y ^ ) (3) L(y, \\hat{y})=-y \\log \\hat{y}-(1-y) \\log (1-\\hat{y}) \\tag{3} L(y,y^)=−ylogy^−(1−y)log(1−y^)(3)
FM 层权重更新方式:
∂ L ( y , y ^ ) ∂ W 0 i = ∂ L ( y , y ^ ) ∂ z i ∂ z i ∂ W 0 i = ∂ L ( y , y ^ ) ∂ z i x [ start i : end i ] W 0 i ← W 0 i − η ⋅ ∂ L ( y , y ^ ) ∂ z i x [ start i : end i ] (4) \\begin{aligned} \\frac{\\partial L(y, \\hat{y})}{\\partial \\boldsymbol{W}_{0}^{i}} &=\\frac{\\partial L(y, \\hat{y})}{\\partial \\boldsymbol{z}_{i}} \\frac{\\partial \\boldsymbol{z}_{i}}{\\partial \\boldsymbol{W}_{0}^{i}}=\\frac{\\partial L(y, \\hat{y})}{\\partial \\boldsymbol{z}_{i}} \\boldsymbol{x}\\left[\\operatorname{start}_{i}: \\text { end }_{i}\\right] \\\\ \\boldsymbol{W}_{0}^{i} & \\leftarrow \\boldsymbol{W}_{0}^{i}-\\eta \\cdot \\frac{\\partial L(y, \\hat{y})}{\\partial \\boldsymbol{z}_{i}} \\boldsymbol{x}\\left[\\operatorname{start}_{i}: \\text { end }_{i}\\right] \\end{aligned}\\tag{4} ∂W0i∂L(y,y^)W0i=∂zi∂L(y,y^)∂W0i∂zi=∂zi∂L(y,y^)x[sta以上是关于19推荐系统11FM与深度学习模型的结合的主要内容,如果未能解决你的问题,请参考以下文章