现代信号处理01 -概率论与随机过程回顾
Posted Ciaran-byte
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了现代信号处理01 -概率论与随机过程回顾相关的知识,希望对你有一定的参考价值。
概率论与随机过程回顾
文章目录
1. 统计模型的相关概念
1.1 统计实验(不确定性)
我们认同不确定性的存在,是人类对自身无知的妥协 – 爱因斯坦
重复进行随机实验
1.2 样本点
是统计实验可能出现的所有结果
1.3 样本空间Ω
所有样本点的集合
1.4 概率
样本空间可以赋予的一些数值,是样本点在统计实验中出现的可能性的大小。
1.5.统计模型是先验的
所有这一切都是先验的,也就是在使用概率论工具之前,他们就是存在的
2. 概率和统计的差异
2.1 联系
共用了同一套符号,而对于处理思路,解决的问题等完全是风马牛不相及
2.2 差异
2.3.1 概率和统计问题的三要素
2.3.1.1 model-模型
统计模型:统计模型包括了1中的所有内容,模型包括的问题如
- 样本空间是什么
- 样本点的概率是什么
2.3.1.2 data-数据
数据是上帝造的,模型是人造的,二者有层级关系
从数据得出模型的过程就是统计
2.3.1.3 decision-决策
有了模型之后,可用模型来推断、预测、判别。
使用模型做出决策的过程,叫概率。
因此使用概率的时候,模型是已知的,因此是先验的
2.3.2 关系图
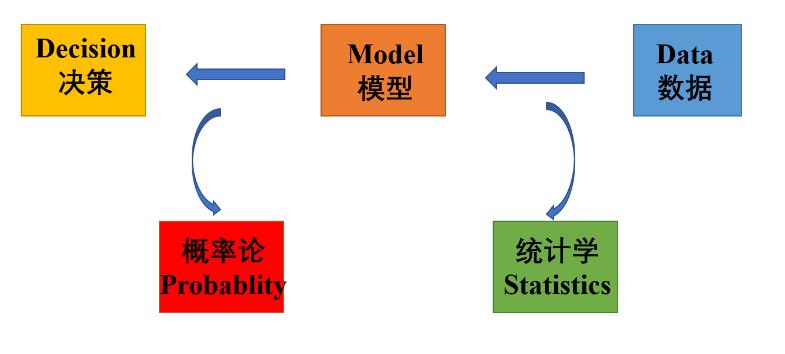
3. 样本空间的重要性
3.1 贝朗特悖论
样本空间选择的正确性对于概率统计来说是非常重要的,比如我们以bertrand paradox(贝特朗悖论)来进行说明
贝朗特悖论描述的是,给定了一个圆,里面有一个内接正三角形,在圆里面随机取一条弦,弦的长度比内接三角形变长长的概率是多少
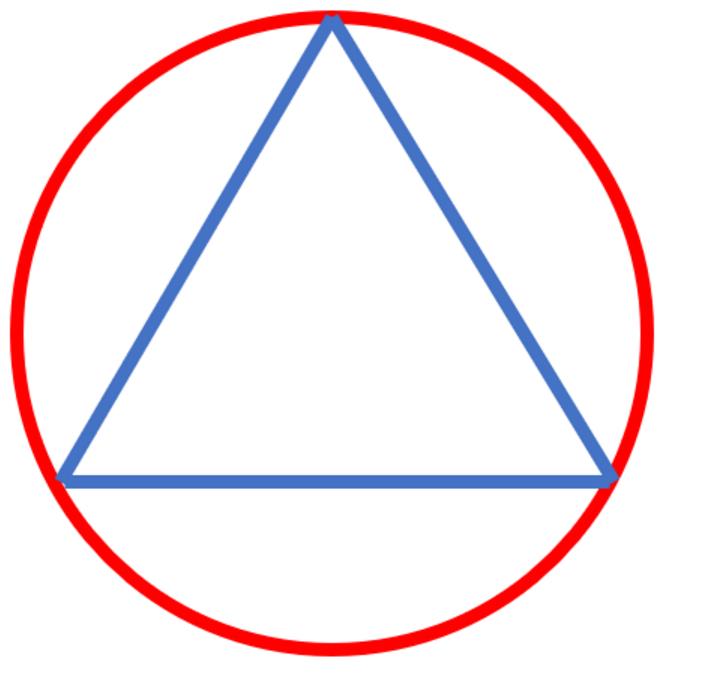
3.1.1 解法一
如果我们固定一个端点去找另外一个端点
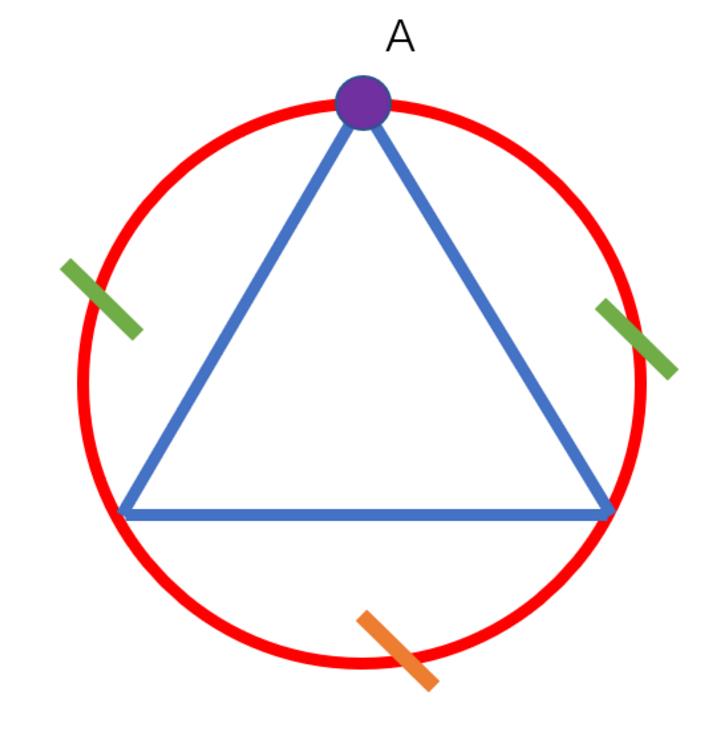
假设从A点出发去寻找另外一点端点,显然当另外一个端点在橙色标记圆弧段的时候成立,概率是
1 3 \\frac{1}{3} 31
3.1.2 解法二
我们也可以固定弦中点去选,假设点A是弦的中点,当弦A在三角形内切圆内的时候,显然经过中点A的弦会比正三角形边长长,这个概率等于内切圆和外接圆的面积比,也就是
1
4
\\frac{1}{4}
41
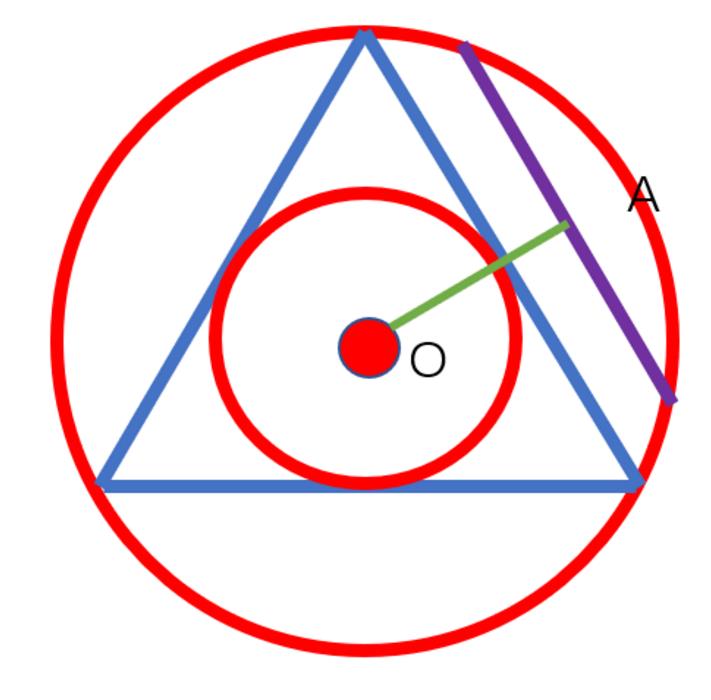
3.1.3 解法三
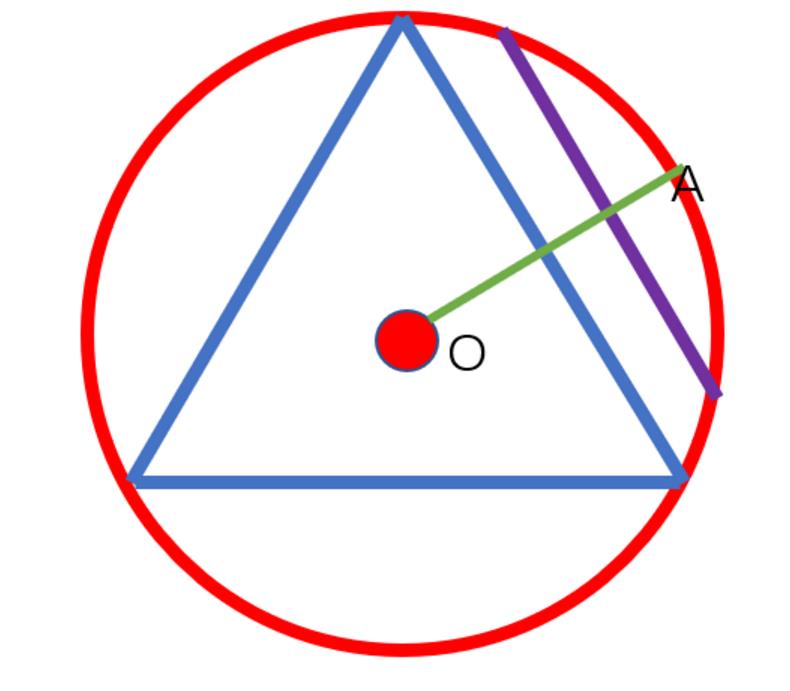
还是固定弦中点,这次比较的对象是半径,如果弦中点在半径的靠近圆心的一半,显然得到的弦长比三角形半径长。因此概率是
1 2 \\frac{1}{2} 21
3.2 结论
上面的所有结果都是对的,因为选点的基础是不一样的。也就是样本空间的选取不同。因此所有的决策都是基于模型在研究问题,模型不同得到的决策不同是很正常的事情,因为概率本来就是在模型的基础上去做的决策。
4.概率相关的概念
4.1 随机变量
随机变量一点随机性都没有,是从样本空间映射到实数轴的一个确定性的函数。
随机变量起到了样本空间量化的作用,把样本空间变成数。因为只有把问题变成了数,才能用数学工具进行处理。比如硬币正面朝上*硬币反面朝上是没有意义的
4.2 分布
P(Z=x)的含义是,概率只能定义在样本空间的样本点上。
P ( Z = x ) = P ( w ∈ Ω ∣ Z ( w ) = x ) P(Z=x)=P({w\\in\\Omega|Z(w)=x}) P(Z=x)=P(w∈Ω∣Z(w)=x)
只有样本点在统计实验中是不确定的,从样本点之后的所有问题都不是随机的。
概率是模型的一部分,是一个先验结果。
概率的另外一个名字就是分布。分布对应的是随机变量,概率对应的是样本点,他们表达的都是同一个模型。不同的随机变量,不同的分布就代表了不同的统计实验和不同的可能性的大小。
4.3 连续与离散
如果随机变量是离散的,意味着样本空间是可数的。可数就是与自然数的真子集一一对应。
w 1 , w 2 , w 3.... {w1,w2,w3....} w1,w2,w3....
如果随机变量是连续的,意味着样本空间就是实数轴
集合只有两种状态,要么可数,要么连续。
4.4 概率密度
4.4.1 概率的累加性
概率的特性中,最重要的就是可加性。
概率最重要的特性就是可加性。不确定性是可以加起来的。
比如对于离散的情况,事件A发生的概率就是其子集Xk发生概率的求和
P ( A ) = ∑ x k ∈ A P ( Z = X k ) P(A)=\\sum_{x_k\\in A}P(Z=X_k) P(A)=xk∈A∑P(Z=Xk)
而对于连续的情况,实际上就是累加符号变成了积分符号
P ( A ) = ∫ A f Z ( x ) d x P(A) = \\int_A f_Z(x)dx P(A)=∫AfZ(x)dx
其中这个f(x)函数可以与概率进行相关联,这个函数叫做概率密度。
4.4.2 概率与概率密度的区别
连续分布函数的概率密度与离散的样本点的概率并不是一回事。原因在于,如果是连续的随机变量,某一点概率的取值一定是0。
f z ( x ) = P ( Z = x ) = 0 f_{z}(x) \\cancel{=} P(Z=x)=0 fz(x)= P(Z=x)=0
4.4.3 概率与概率密度的联系
概率密度与概率的关联在于,连续函数某一点的概率,近似等于某一点上一段的概率。这一段的概率,根据概率的定义,就是一个微积分。这个微积分又可以近似为f(x)*△x。一般来说,问题进行近似化研究会不严禁,但是离散和连续问题之间天然存在这样一个鸿沟。
P ( Z = x ) ≈ P ( x < Z < x + Δ x ) = ∫ x x + Δ x f z ( s ) d s ≈ f z ( x ) ∗ Δ x P(Z=x) \\approx P(x<Z<x+\\Delta x) \\\\ = \\int_x^{x+\\Delta x} f_z(s)ds \\\\ \\approx f_z(x)*\\Delta x P(Z=x)≈P(x<Z<x+Δx)=∫xx+Δxfz(s)ds≈fz(x)∗Δx
密度和概率都是模型的一部分。
密度的原函数叫做分布函数
F Z ( x ) = ∫ f Z ( s ) d s F_Z(x) = \\int f_Z(s)ds FZ(x)=∫fZ(s)ds
5.几种典型的分布
5.1 离散的分布
5.1.1 伯努利模型(两点分布) Bernoalli
Z ∼ { x 1 x 2 P 1 − P } ( 0 ≤ P ≤ 1 ) Z \\sim\\begin{Bmatrix} x_1 & x_2 \\\\ P & 1-P \\end{Bmatrix} \\quad (0\\leq P \\leq 1) Z∼{x1Px21−P}(0≤P≤1)
5.1.2 射击模型(二项分布) Binormal
二项分布就是做了n次伯努利实验以后的分布
问题描述:一共打了n枪,每一枪的概率都是p,打中k枪的概率是多少
Z ∼ B ( n , p ) P ( Z = k ) = { n k } ∗ P k ∗ ( 1 − P ) n − k Z \\sim B(n,p) \\\\ P(Z=k)=\\begin{Bmatrix} n \\\\ k \\end{Bmatrix}*P^k*(1-P)^{n-k} Z∼B(n,p)P(Z=k)={nk}∗Pk∗(1−P)n−k
5.1.3 泊松分布 Poisson
5.1.3.1 泊松分布与二项分布的关系
P ( Z = k ) = λ k k ! e x p ( − λ ) k = 0 , 1 , 2... P(Z=k)= \\frac{\\lambda^k}{k!}exp(-\\lambda) \\quad\\quad k=0,1,2... P(Z=k)=k!λkexp(−λ)k=0,1,2...
泊松分布其实与二项分布是一脉相承的。
我们让二项分布的P趋近于0,也就是射中率接近0,为了补偿,让实验次数n趋近于无穷大。同时让np是个常数
P ( Z = k ) = { n k } ∗ P k ∗ ( 1 − P ) n − k P → 0 , n → ∞ , n ∗ P = λ P(Z=k)=\\begin{Bmatrix} n \\\\ k \\end{Bmatrix}*P^k*(1-P)^{n-k} \\quad\\quad P\\rightarrow 0,n\\rightarrow \\infty,n*P = \\lambda P(Z=k)={nk}∗Pk∗(1−P)n−kP→0,n→∞,n∗P=λ
5.1.3.2 公式推导
先把公式拆分为四个部分 以上是关于现代信号处理01 -概率论与随机过程回顾的主要内容,如果未能解决你的问题,请参考以下文章
{
n
k
}
∗
P
k
∗
(
1
−
P
)
n
−
k
=
n
!
k
!
∗
(
n
−
k
)