现代信号处理 03 - 线性估计
Posted Ciaran-byte
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了现代信号处理 03 - 线性估计相关的知识,希望对你有一定的参考价值。
线性估计
文章目录
1. 问题引入
在之前的章节中,我们引入了克拉美罗界CRLB,用来评估使用最小方差无偏估计MVUE能够达到什么程度。在这之后,我们希望能够找到一些简单好用的方法,能够对数据进行估计。其中历史最悠久,使用最广泛的,就是线性估计了。
我们提出这样一个问题,下面这条曲线,是一组随时间变化的数据形成的,我们如何估计这条曲线的表达式呢?

我们观测的对象,其实由两部分组成,一部分是由其内部机制引起的数据变化,另一部分是由于噪声引起的数据变化。我们希望能够得到这组数据背后的变化规律,因此我们要对他进行估计。通过直觉,我们感觉这是一条直线,因此我们建立如下模型,进行参数估计
按理来说,直线的模型是,其中A和B是需要估计的参数
Z ( t ) = A + B t Z(t) = A +Bt Z(t)=A+Bt
但是实际上,我们的数据是包含噪声的,因此,我们在直线的基础上叠加一个随机噪声
Z ( t ) = A + B t + N ( t ) Z(t) = A +Bt +N(t) Z(t)=A+Bt+N(t)
我们对Z进行采样。其中\\Delta t是采样间隔,得到以下的数据
Z 1 , . . . , Z n Z k = A + B ∗ k ∗ Δ t + N k , N k = N ( k Δ t ) Z_1,...,Z_n \\quad \\quad Z_k = A + B*k*\\Delta t +N_k ,\\quad N_k = N(k\\Delta t) Z1,...,ZnZk=A+B∗k∗Δt+Nk,Nk=N(kΔt)
这样我们就有了一个模型,这是一个典型的线性模型。我们可以有很多种求解方法。下面,我们将采用不同思路进行线性模型的估计
2. 问题求解
2.1 线性拟合的方法进行参数求解
2.1.1 目标函数的确立
首先我们用线性拟合的方式进行求解,先把已知条件抄下来
Z 1 , . . . , Z n Z k = A + B ∗ k ∗ Δ t + N k , N k = N ( k Δ t ) Z_1,...,Z_n \\quad \\quad Z_k = A + B*k*\\Delta t +N_k ,\\quad N_k = N(k\\Delta t) Z1,...,ZnZk=A+B∗k∗Δt+Nk,Nk=N(kΔt)
我们在每个点计算模型与采样之间的误差,然后把误差加在一起。这是一个与A和B都有关的函数
∑
k
=
1
n
(
Z
k
−
A
−
B
∗
k
∗
Δ
t
)
2
∼
g
(
A
,
B
)
\\sum _{k=1}^n(Z_k -A -B*k*\\Delta t)^2 \\sim g(A,B)
k=1∑n(Zk−A−B∗k∗Δt)2∼g(A,B)
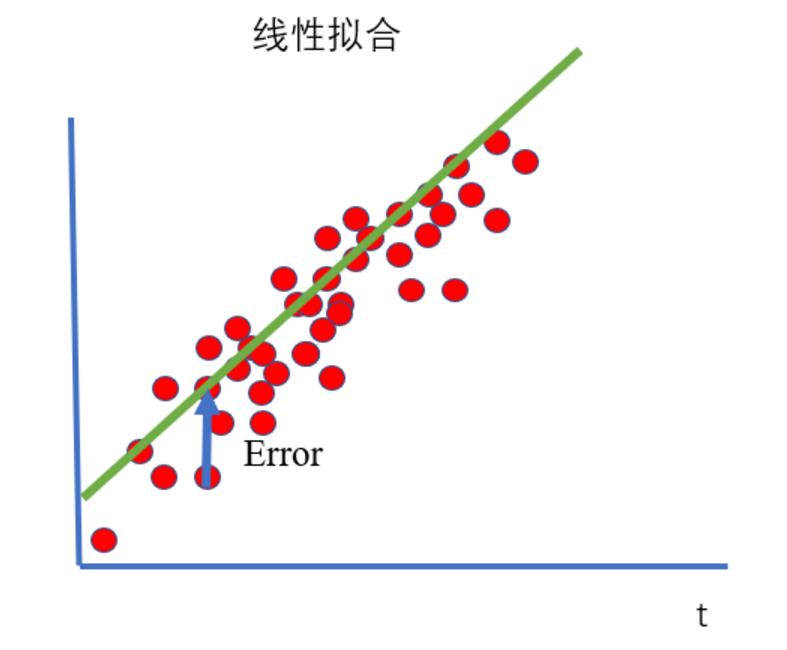
我们进行最优估计的原则就是,我们要让数据点与模型垂直距离的平方和最小
= > m i n [ g ( A , B ) ] => min [g(A,B)] =>min[g(A,B)]
直接从平方和开始计算非常麻烦,我们用更加流行的方法,我们这个模型变成向量的形式进行表示
- 采样数据Z的表示
Z = ( Z 1 , . . . Z n ) T Z = (Z_1,...Z_n)^T Z=(Z1,...Zn)T
- 估计量θ的表示
θ = ( A , B ) T \\theta = (A,B)^T θ=(A,B)T
- 矩阵H的表示
假设H是一个nx2矩阵
H ∈ R n x 2 H = ( 1 Δ t . . . . . . 1 n Δ t ) H \\in R^{nx2} \\\\ H=\\begin{pmatrix} 1 & \\Delta t \\\\ ... & ... \\\\ 1 & n \\Delta t \\end{pmatrix} H∈Rnx2H=⎝⎛1...1Δt...nΔt⎠⎞
- 噪声N的表示
N = ( N 1 , . . . , N n ) T N = (N_1,...,N_n)^T N=(N1,...,Nn)T
我们对模型进行向量化表示
Z
=
H
θ
+
N
(
1
)
Z = H \\theta +N \\quad\\quad\\quad(1)
Z=Hθ+N(1)
目标函数也进行向量化表示
g
(
θ
)
=
(
H
θ
−
N
)
T
(
H
θ
−
N
)
(
2
)
g(\\theta) = (H\\theta-N)^T (H\\theta-N) \\quad\\quad\\quad(2)
g(θ)=(Hθ−N)T(Hθ−N)(2)
g
(
θ
)
=
Z
T
∗
Z
−
θ
T
H
T
Z
−
Z
T
H
θ
+
θ
T
H
T
H
θ
(
3
)
g(\\theta) = Z^T*Z - \\theta^TH^TZ - Z^T H\\theta+\\theta^TH^TH\\theta \\quad\\quad\\quad(3)
g(θ)=ZT∗Z−θTHTZ−ZTHθ+θTHTHθ(3)
2.1.2 梯度的性质
因为我们需要用到矢量求梯度的性质,这里引入一些性质
矢量求梯度的结果。假设h是θ的函数,h是个矩阵或者矢量都行,则对其求梯度,结果就是其雅克比行列式
∇
θ
(
h
(
θ
)
)
=
(
∂
h
1
∂
θ
1
.
.
.
∂
h
1
∂
θ
n
.
.
.
.
.
.
.
.
.
∂
h
m
∂
θ
1
.
.
.
∂
h
m
∂
θ
n
)
\\nabla_{\\theta}(h(\\theta)) = \\begin{pmatrix} \\frac{\\partial h_1}{\\partial \\theta _1} & ...&\\frac{\\partial h_1}{\\partial \\theta _n} \\\\ ... & ... &... \\\\ \\frac{\\partial h_m}{\\partial \\theta _1} & ... & \\frac{\\partial h_m}{\\partial \\theta _n} \\end{pmatrix}
∇θ(h(θ))=⎝⎛∂θ1∂h1...< 以上是关于现代信号处理 03 - 线性估计的主要内容,如果未能解决你的问题,请参考以下文章