P2480 [SDOI2010]古代猪文(数论好题)

Posted Jozky86

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了P2480 [SDOI2010]古代猪文(数论好题)相关的知识，希望对你有一定的参考价值。

P2480 [SDOI2010]古代猪文

题意：

给你n和g，求 g ∑ d ∣ n C n d   m o d   p g^{\\sum_{d|n}C_{n}^{d}}\\bmod p g∑d∣n​Cnd​modp
p=999911659

题解：

这个一个综合性很强的数论题
涉及到欧拉定理，Lucas定理，中国剩余定理，挺好的一个题
首先根据欧拉定理推论：

若正整数a，n互质，对于任意的正整数b，有 a b ≡ a b   m o d   ϕ ( n ) (   m o d   n ) a^b \\equiv a^{b\\bmod \\phi(n)}(\\bmod n) ab≡abmodϕ(n)(modn)

所以
= g ∑ d ∣ n C n d   m o d   ϕ ( p )   m o d   p =g^{\\sum_{d|n}C_{n}^{d}\\bmod \\phi(p)}\\bmod p =g∑d∣n​Cnd​modϕ(p)modp
ϕ ( p ) = p − 1 = 999911658 \\phi(p)=p-1=999911658 ϕ(p)=p−1=999911658
= g ∑ d ∣ n C n d   m o d   999911658   m o d   p =g^{\\sum_{d|n}C_{n}^{d}\\bmod 999911658}\\bmod p =g∑d∣n​Cnd​mod999911658modp
现在的关键在于求 ∑ d ∣ n C n d   m o d   999911658 \\sum_{d|n}C_{n}^{d}\\bmod 999911658 ∑d∣n​Cnd​mod999911658,
999911658不是质数，咋搞？那我们可以将其质因子分解：999911658=4679 * 3 * 2 *35617，每个质因子的次数都是1，所以我们只需要用CRT来求解如下的方程组

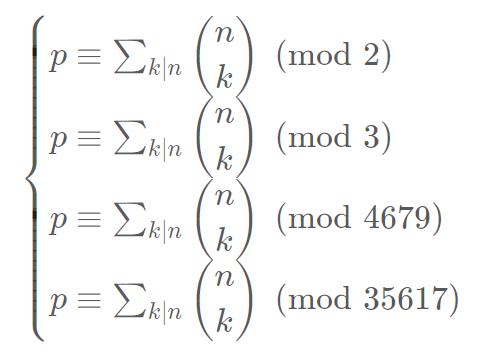
求出p后，最后再一个快速幂输出答案

CRT：

inline ll CRT()
{
	ll ans=0;
	for(register int i=1;i<=cnt;i++)
	{
		ll M=mod/p[i],t=qpow(M,p[i]-2,p[i]);
		ans=(ans+a[i]%mod*t%mod*M%mod)%mod;
	}
	return (ans+mod)%mod;
}

Lucas组合数：

ll C(int a, int b, ll mod)
{
    if (b > a)
        return 0;
    return fac[a] % mod * inv[b] % mod * inv[a - b] % mod;
}
ll Lucas(ll n, ll m, ll p)
{
    if (m == 0)
        return 1;
    return Lucas(n / p, m / p, p) * C(n % p, m % p, p) % p;
}

递推求阶乘逆元

( n − 1 ) ! × n [ n ! ] − 1 ≡ 1   m o d   p (n−1)!×n[n!]^{−1}≡1 \\bmod p (n−1)!×n[n!]−1≡1modp

void init() {
	fact[0] = 1;
	for (int i = 1; i < maxn; i++) {
		fact[i] = fact[i - 1] * i %mod;
	}
	inv[maxn - 1] = power(fact[maxn - 1], mod - 2);
	for (int i = maxn - 2; i >= 0; i--) {
		inv[i] = inv[i + 1] * (i + 1) %mod;
	}
}

代码：

but，代码存在问题，还没修改出哪里错了

目前95分，错了第一个点，人傻了

// Problem: P2480 [SDOI2010]古代猪文
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2480
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Data:2021-08-26 15:50:36
// By Jozky

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
void read(){};
template <typename _Tp, typename... _Tps> void read(_Tp& x, _Tps&... Ar)
{
    x= 0;
    char c= getchar();
    bool flag= 0;
    while (c < '0' || c > '9')
        flag|= (c == '-'), c= getchar();
    while (c >= '0' && c <= '9')
        x= (x << 3) + (x << 1) + (c ^ 48), c= getchar();
    if (flag)
        x= -x;
    read(Ar...);
}
template <typename T> inline void write(T x)
{
    if (x < 0) {
        x= ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef LOCAL
    startTime= clock();
    freopen("in.txt", "r", stdin);
#endif
}
void Time_test()
{
#ifdef LOCAL
    endTime= clock();
    printf("\\nRun Time:%lfs\\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
const int maxn= 4e4 + 9;
ll n, g;
ll fac[maxn];
ll inv[maxn];
const int mod= 999911659;
ll p[maxn];
ll c[maxn];
ll a[maxn];
int cnt= 0;
int tot= 0;
ll poww(ll a, ll b, ll mod)
{
    ll ans= 1;
    while (b) {
        if (b & 1)
            ans= ans * a % mod;
        a= a * a % mod;
        b>>= 1;
    }
    return ans % mod;
}
ll exgcd(int a, int b, ll &x, ll &y)
{
    if (b == 0) {
        x= 1;
        y= 0;
        return a;
    }
    int gcd= exgcd(b, a % b, x, y);
    ll t= x;
    x= y;
    y= t - a / b * y;
    return gcd;
}
ll CRT(int k, ll a[], ll r[], ll mod)
{
    ll n= 1, ans= 0;
    ll x,y;
    for (int i= 1; i <= k; i++)
        n= n * r[i];
    for (int i= 1; i <= k; i++) {
        ll m= n / r[i];
        exgcd(m, r[i], x, y);
        ans= (ans + a[i] % mod * m % mod * x % mod) % mod;
    }
    return (ans % mod + mod) % mod;
}
ll C(int a, int b, ll mod)
{
    if (b > a)
        return 0;
    return fac[a] % mod * inv[b] % mod * inv[a - b] % mod;
}
ll Lucas(ll n, ll m, ll p)
{
    if (m == 0)
        return 1;
    return Lucas(n / p, m / p, p) * C(n % p, m % p, p) % p;
}
void init(int p)
{
    fac[0]= 1;
    for (int i= 1; i < p; i++) {
        fac[i]= fac[i - 1] * i % p;
    }
    inv[p]=0;
	inv[p-1]=poww(fac[p-1],p-2,p);
	for(register int i=p-2;i>=0;i--)
		inv[i]=inv[i+1]*(i+1)%p;
}
void calc(int x)
{
    init(p[x]);
    for (int i= 1; i <= tot; i++) {
        a[x]= (a[x] + Lucas(n, c[i], p[x])) % p[x];
    }
}

int main()
{
    //rd_test();
    cin >> n >> g;
    if (g % mod == 0) {
        printf("0--\\n");
        return 0;
    }
    ll phi= mod - 1;
    for (int i= 2; i * i <= (mod - 1); i++) { //对mod-1进行质因子分解
        if (phi % i == 0) {
            p[++cnt]= i;
            while (phi % i == 0)
                phi= phi / i;
        }
    }
    if (phi != 1)
        p[++cnt题解P2480 [SDOI2010]古代猪文 - 卢卡斯定理 - 中国剩余定理


 洛谷P2480 [SDOI2010]古代猪文


 P2480 [SDOI2010]古代猪文  Lucas+CRT合并


 Luogu P2480 [SDOI2010]古代猪文 卢卡斯+组合+CRT


 1951: [Sdoi2010]古代猪文|数论大合集


 bzoj 1951 [Sdoi2010]古代猪文（数论知识）