Codeforces Round #741 Div. 2 A B C D1 D2
Posted a碟
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Codeforces Round #741 Div. 2 A B C D1 D2相关的知识，希望对你有一定的参考价值。
目录
四题下班，每次D2都做不出或者没啥时间了…
大胆假设，猜到结论就可以冲了(bushi
A. The Miracle and the Sleeper
题目链接
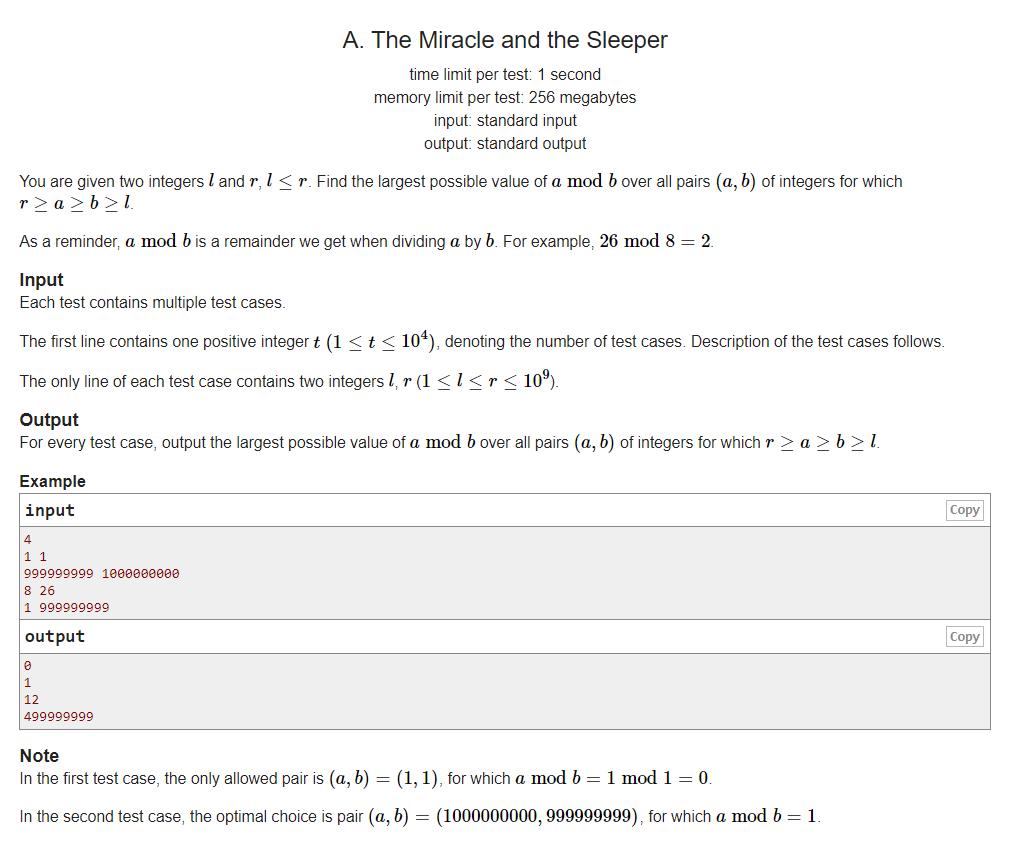
题意： 已知两个整数
l
l
l和
r
r
r,
l
≤
r
l≤r
l≤r。求所有
r
≥
a
≥
b
≥
l
r≥a≥b≥l
r≥a≥b≥l的整数对
(
a
,
b
)
(a,b)
(a,b)中
a
a
a
m
o
d
mod
mod
b
b
b的最大可能值。
分析： 在给定的
l
,
r
l,r
l,r中，选择
r
≥
a
≥
b
≥
l
r≥a≥b≥l
r≥a≥b≥l，的
a
,
b
a,b
a,b使得
a
m
o
d
b
a mod b
amodb最大。可以想到如果有数
x
x
x，使得
r
r
r
÷
\\div
÷
x
=
1......
x
−
1
x=1......x-1
x=1......x−1，这样的
x
x
x最大是多少？
r
=
2
x
−
1
r=2x-1
r=2x−1，
x
=
(
r
+
1
)
/
2
x=(r+1)/2
x=(r+1)/2，如果
l
≤
(
r
+
1
)
/
2
l \\leq (r+1)/2
l≤(r+1)/2，那么答案就是
(
r
+
1
)
/
2
−
1
(r+1)/2-1
(r+1)/2−1。
否则，即
l
≥
(
r
+
1
)
/
2
l \\geq (r+1)/2
l≥(r+1)/2时，只能这样构造，
r
÷
l
=
1.....
r
−
l
r \\div l=1.....r-l
r÷l=1.....r−l，答案也就是
r
−
l
r-l
r−l。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
int main()
{
int t;scanf("%d",&t);
while(t--){
int l,r;scanf("%d %d",&l,&r);
if((r+1)/2>=l)printf("%d\\n",(r+1)/2-1);
else printf("%d\\n",r%l);
}
return 0;
}
B. Scenes From a Memory
题目链接
题意： 给定一个正整数n，它在十进制表示法中不包含零。问：这个数最多可以去掉多少位数字，这样这个数就不是质数了。
分析： 仔细分析，从一大串数字删掉最多的数字后，剩下的数是一个合数。看了样例之后大胆猜测剩下的位数不是1就是2，然后莽了一发对了(不要学我)。
其实仔细分析，因为答案保证一定有解，假设剩下的数是三位。能找到一个三位数，使得这个三位数是一个合数，但是其任意两个数组成的两位数不是合数吗。感觉证明不是很科学。起床之后再想想…起床了
我们来证明一下，如果一个数是三位数，你总是可以从其中至少删除一个数来得到一个数不是质数。
法一：可以通过对所有三位数的数字爆搜来得到解，我没有写了，大家可以试试。
法二：如果一个数中包含
1
，
4
，
6
，
8
，
9
1，4，6，8，9
1，4，6，8，9，那么其中任意一个数字就是答案，这几个数都是非素数。
如果一个三位数中没有这些数字呢？也就是只包含
2
，
3
，
5
，
7
2，3，5，7
2，3，5，7。
- 如果这个数中，存在 2 2 2或者 5 5 5不在第一位，那么可以删掉一个数变成合数。比如 752 752 752， 723 723 723中选择 75 75 75和 72 72 72。
- 如果是存在任意两个相同的数，比如 22 ， 33 ， 55 ， 77 22，33，55，77 22，33，55，77，这些数都是合数。
- 同时包含 5 ， 7 5，7 5，7的数，是肯定能够构成 57 57 57或 75 75 75，能被 3 3 3整除，是合数。
- 剩下的情况就是，
273
，
237
273，237
273，237，删除
3
3
3即可构成
27
27
27，能被
3
3
3整除，也是合数
所以上述就证明了，留下来的数字肯定不超过两位，然后直接暴力模拟就行了。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=55;
char s[N];
bool check(int x){
if(x<=3)return x>1;
if(x%2==0||x%3==0)return 0;
for(int i=5;i<=sqrt(x);i+=6){
if(x%i==0||x%(i+2)==0)return 0;
}
return 1;
}
int main()
{
int t;scanf("%d",&t);
while(t--){
int n,flag=0;scanf("%d",&n);
scanf("%s",s+1);
for(int i=1;s[i];i++){
int p=s[i]-'0';
if(!check(p)){
printf("%d\\n%d\\n",1,p);
flag=1;
break;
}
}
if(flag)continue;
for(int i=1;s[i];i++){
for(int j=i+1;s[j];j++){
int p=(s[i]-'0')*10+s[j]-'0';
if(!check(p)){
printf("%d\\n%d\\n",2,p);
flag=1;
break;
}
}
if(flag)break;
}
}
return 0;
}
C. Rings
题目链接
题意： 给定一个01串，从中选出两个长度大于等于
⌊
n
2
⌋
\\lfloor \\frac{n}{2} \\rfloor
⌊2n⌋的区间
t
t
t和
w
w
w，使得两个区间所构成的十进制数满足
f
(
t
)
=
f
(
w
)
⋅
k
f(t)=f(w)⋅k
f(t)=f(w)⋅k。(
f
(
x
)
f(x)
f(x)就是
x
x
x的十进制数，
k
k
k为非负整数)
分析： 很巧妙的题目，这个题目就分为两种情况讨论。
- 全为 1 1 1，这种情况只需要输出长度大于等于 n / 2 n/2 n/2的两个区间，且这两个区间长度为倍数关系即可。我直接输出了 1 , n / 2 ∗ 2 ; 1 , n / 2 1,n/2*2;1,n/2 1,n/2∗2;1,n/2
- 不全为
1
1
1，在
0001000
0001000
0001000中，可以选择
0001000
,
001000
0001000,001000
0001000,001000，在
100100
100100
100100中，选择
00100
00100
00100，
0100
0100
0100。可以看出些什么？
从左往右在前面一半的数中，找到第一个 0 0 0，可以看出 0 x 0x 0x( x x x是0右边的任意 01 01 01串)和 x x x是相等的。所以直接从当前0的位置，直接输出答案到结尾，另一个部分就是当前0后面的位置到结尾。
在后面一半中，从右往左找一遍。同理， 1111000 1111000 1111000中选择 1111000 1111000 1111000和 111100 111100 111100是可行解。 x 0 x0 x0(x是0左边的任意01串)等于 x × 2 x \\times 2 x×2，所以选择的两个部分分别是，从首位到当前0的位置，从首位到当前0前面的一个位置。
非常巧妙的题目。
代码：
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int N=2e4+5;
char s[N];
int main()
{以上是关于Codeforces Round #741 Div. 2 A B C D1 D2的主要内容，如果未能解决你的问题，请参考以下文章
Codeforces Round #741 Div. 2 A B C D1 D2
Codeforces Round #741 Div. 2 A B C D1 D2
Codeforces Round #741 div.2 A-F题解
Codeforces Round #741 Div. 2 A B C D1 D2