[数值计算-13]：多项式插值多项式几何图形与线性方程组求解

Posted 2021-09-10 文火冰糖的硅基工坊

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119941466

---

目录

第1章 案例与建模

1.1 案例说明

 1.2 建模与预测​

第2章 插值

2.1 什么是插值

2.2 插值的关键是如何构建插值函数！！！

第3章 多项式插值 

3.1 什么是多项式插值

3.2 多项式函数的唯一性

3.3 求多项式插值函数的本质是求线性方程组

3.4 求线性方程组的解的方法

3.5 多项式插值的优缺点

第4章 多项式函数图形案例

---

---

第1章 案例与建模

1.1 案例说明

 1.2 建模与预测

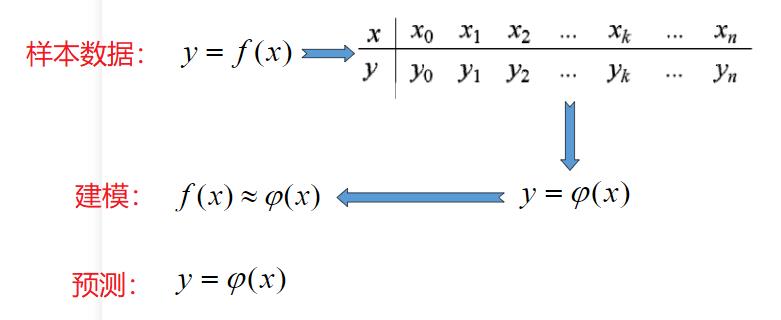
第2章 插值

2.1 什么是插值

 

 这里的插值条件是：插值函数要经过所有现有的样本点！！！

 这个插值条件的优点：在样本点的误差为0。

 这个插值条件的缺点：这个条件还是比较苛刻的，导致选用高次函数，且样本点的个数越多，函数的最高次的次数越高。

2.2 插值的关键是如何构建插值函数！！！

第3章 多项式插值 

3.1 什么是多项式插值

3.2 多项式函数的唯一性

3.3 求多项式插值函数的本质是求线性方程组

 

 N+1个未知数：an，an-1, ...........a0

 N+1个方程，组成两个方程组

未知数的次数都是1

因此上述方式组称为N个未知数的线性方程组。

3.4 求线性方程组的解的方法

（1）解析法

• 直接法
• 高斯消元法
• 平方根法
• 追赶法

（2）数值法

• 雅可比迭代
• 松弛法迭代

 详细的解法步骤，请参考相关文章。

3.5 多项式插值的优缺点

（1）优点

• 直观、容易理解

（2）缺点

• 当采样点非常多时，需要求解的方程的未知数个数就就非常多，计算量非常庞大，造成计算上的困难和效率上的浪费。

第4章 多项式函数图形案例

#导入库
from math import *
import time
import numpy as np
import matplotlib.pyplot as plt

# 函数图形
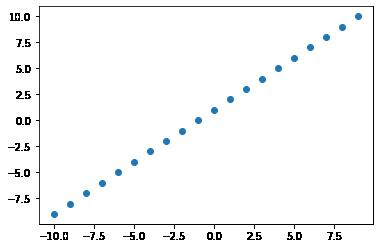
x_data = np.arange(-10, 10, 1)

# 1次多项式
def f1(x):
    return(x+1) 

y1_data = f1(x_data)
plt.scatter(x_data, y1_data)

# 2次多项式
def f2(x):
    return(x**2 + x + 1) 

y2_data = f2(x_data)
plt.scatter(x_data, y2_data)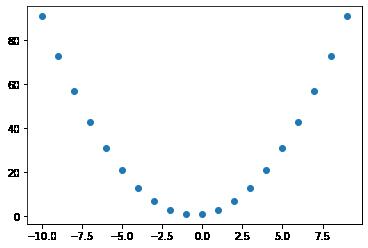

# 3次多项式
def f3(x):
    return(x**3 + x**2 + x + 1) 

y3_data = f3(x_data)
plt.scatter(x_data, y3_data)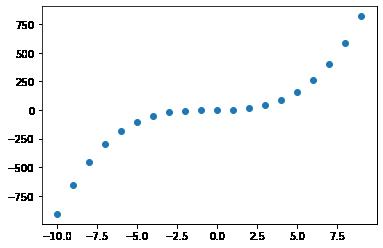

# 4次多项式
def f4(x):
    return(x**4 + x**3 + x**2 + x + 1) 

y4_data = f4(x_data)
plt.scatter(x_data, y3_data)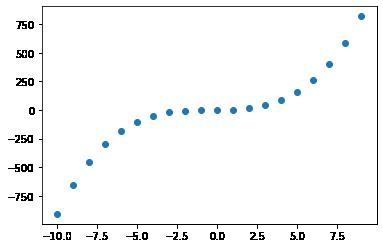

# 10次多项式
def f10(x):
    return(x**10 + x**9 + x**8 + x**7 + x**6 + x**5 + x**4 + x**3 + x**2 + x + 1) 

y10_data = f10(x_data)
plt.scatter(x_data, y10_data)

# 11次多项式
def f11(x):
    return(x**11 + x**10 + x**9 + x**8 + x**7 + x**6 + x**5 + x**4 + x**3 + x**2 + x + 1) 

y11_data = f11(x_data)
plt.scatter(x_data, y11_data)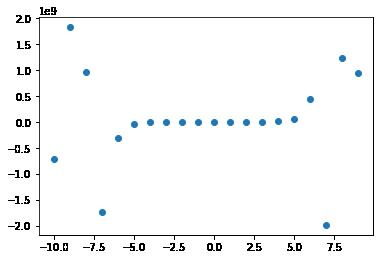

---

作者主页(文火冰糖的硅基工坊)：https://blog.csdn.net/HiWangWenBing

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/119941466