数学建模学习（30）：神经网络算法模型之感知器，详细讲解+完整代码，包教包会！

Posted 2021-09-10 川川菜鸟

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数学建模学习（30）：神经网络算法模型之感知器，详细讲解+完整代码，包教包会！相关的知识，希望对你有一定的参考价值。

一、前言描述

1.1几句话描述该模型

我不会说一句废话，因此下面我讲到的每一个函数每一步搭建都是很重要的，因此你要专注认真学习，自己敲或者复制粘贴，重点在于理解。当然你要问我，怎么不介绍概念？高大上概念你要看得懂嘛，不如直接上实际的。

神经网络有很多种，我都会在后续的文章依次讲解，本篇讲解感知器，具体包括：

感知器
线性网络
BP网络
径向基函数网络
竞争性神经网络
自组织网络和学习向量量化网络
反馈网络

1.2搭建步骤

每种神经网络应用场景均独一无二，但是开发网络通常遵循下列步骤：

访问和准备数据
创建神经网络
配置网络的输入和输出
调整网络参数（权重和偏差）以优化性能
训练网络
验证网络的结果
将网络集成到生产系统中

二、通用神经网络工具箱函数

这是通用，再次强调，通用函数，也就是说，这是所有神经网络类型都可以用的函数。比如训练函数train,仿真函数sim等。

一.perceptron简单的单层二元分类器

语法：

perceptron(hardlimitTF,perceptronLF)

如果不传入参数，hardlimitTF—硬限制传递函数’hardlim’（默认）；perceptronLF—感知器学习规则（默认）'learnp’感知器学习规则。
这个例子展示了如何使用感知器来解决一个简单的分类逻辑或问题：

%perceptron函数
x = [0 0 1 1; 0 1 0 1];
t = [0 1 1 1];
NET = perceptron;%创建二元分类器
net = train(NET,x,t);
view(net)	%view函数就是查看视图
y = net(x);

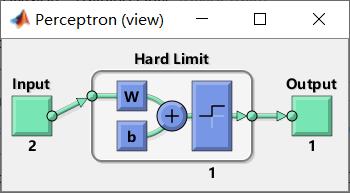
二、configure配置网络

这里我们要用到configure函数配置网络输入和输出以最佳匹配输入和目标数据。
语法：

net = configure(net,x,t)
net = configure(net,x)
net = configure(net,'inputs',x,i)
net = configure(net,'outputs',t,i)

详细说明

net = configure(net,x,t)获取输入数据x和目标数据t，并配置网络的输入和输出以匹配。

net = configure(net,x) 仅配置输入。

net = configure(net,'inputs',x,i)配置使用索引向量指定的输入i。如果i未指定，则配置所有输入。

net = configure(net,'outputs',t,i)配置用索引向量指定的输出i。如果i未指定，则配置所有目标。

三、init初始化神经网络

语法

net = init(NET)

NET是未经过初始化的神经网络，net是经过初始化的神经网络

四、train训练浅层神经网络

该函数可以训练神经网络，是通用的学习函数，会一直训练知道达到最大学习步数，最小误差或目标等条件后，停止训练。
语法：

trainedNet = train(NET,X,T,Xi,Ai,EW)net根据net.trainFcn 和 训练网络net.trainParam。

[trainedNet,tr] = train(NET,X,T,Xi,Ai,EW) 还返回训练记录。

[trainedNet,tr] = train(NET,X,T,Xi,Ai,EW,Name,Value) 使用由一个或多个名称-值对参数指定的附加选项训练网络。

在调用该函数之前，需要先设定训练书，训练步数，训练目标误差等参数，如果没有设定，train函数调用系统默认的参数训练。
参数详解
输入参数：

NET—需要训练的神经网络
X—神经网络输入
T—神经网络网络目标
Xi—初始输入延迟条件，默认为0
Ai—初始层延迟条件，默认为0
EW—误差权重

输出参数：

trainedNet— 训练好的网络
tr— 训练记录

四.单层神经网络初始化

用到initlay函数。
语法：

net = initlay(NET)
info = initlay('code')

NET是没有初始化的神经网络，net是初始化的神经网络。

五.神经网络单层权值和偏值初始化

用到initnw函数。
语法：

net = initnw(NET,i)

NET是没有初始化的神经网络，i为需要进行权值和偏值进行修正的，net是第i层经过初始化的神经网络。

六.神经网络仿真函数

神经网络完成训练后，其权值与偏值也确认了。利用sim函数可以检测已完成训练的神经网络新的新还能。
语法：

[Y,xf,Af,E]=sim(net,X,Xi,Ai,T)

net是需要训练的神经网络；X为神经网络的输入；Xi为初始输入演示，默认为0；Ai表示初始延时的层延时，默认0；T为训练神经网络的目标输出，默认为0；Y为神经网络的输出；Xf为最终输入延时；Af为最终的延时；E表示网络误差。

七.神经网络输入和函数

我们在这里用到netsum函数。神经网络输入和函数是通过某一层加权输入和偏值相加作为该层的输入。
语法：

N = netsum({Z1,Z2,...,Zn},FP)

其中Zn是S*Q维矩阵。下面是使用该函数将两个权值和一个偏置相加：

%netsum函数使用
z1 = [1, 2, 4; 3, 4, 1];
z2 = [-1, 2, 2; -5, -6, 1];
b = [0; -1];
n = netsum({z1, z2, concur(b, 3)})

得到神经网络输入；

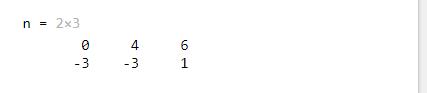
八.权值点积函数

神经网络输入量与权值的点积可以得到加权输入。
语法：

Z = dotprod(W,P,FP)

其中W维权值矩阵;p为输入向量;FP维功能参数（可省略）;Z维权值矩阵与输入向量的点积。
利用该函数求一个点击例子如下：

W = rand(4,3);
P = rand(3,1);
Z = dotprod(W,P)

九.网络输入的积函数

语法：

N = netprod({Z1,Z2,...,Zn})

该函数是将神经网络某一层加权输入和偏值相乘的结果，作为该层的输入。其中Zn为S*Q维矩阵。
这里，netprod组合了两组加权的输入向量：

Z1 = [1 2 4;3 4 1];
Z2 = [-1 2 2; -5 -6 1];
Z = {Z1,Z2};
N = netprod({Z})

返回：

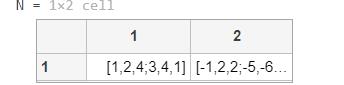
这里将相同的加权输入与偏置向量组合在一起。由于 Z1 和 Z2 各自包含三个并发向量，因此必须使用 concur 创建 B 的三个并发副本，以便所有大小匹配。

B = [0; -1];
Z = {Z1, Z2, concur(B,3)};
N = netprod(Z)

因此，此时全部代码为：

%netprod积函数                          
Z1 = [1 2 4;3 4 1];
Z2 = [-1 2 2; -5 -6 1];
Z = {Z1,Z2};
N = netprod({Z})
B = [0; -1];
Z = {Z1, Z2, concur(B,3)};
N = netprod(Z)

3.1创建一个感知器

x = [0 1 0 1; 0 0 1 1];
t = [0 0 0 1];
net = perceptron;
net = configure(net,x,t);
net.iw{1,1}
net.b{1}

返回：

表示感知器的权值和偏值均为默认值：0。

3.2训练建立的神经网络

%训练建立的神经网络
net = train(net,x,t);
net.iw{1,1}
net.b{1}

返回神经网络训练过程如下：

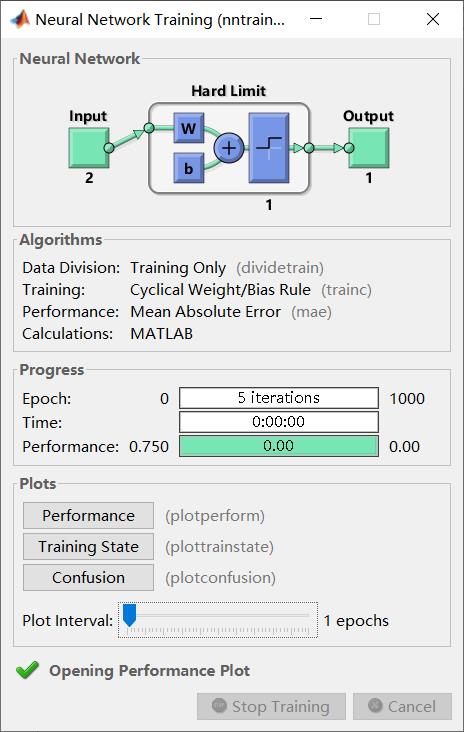
训练后的感知器神经网络权值和偏值分别如下：

3.3重新初始化权重和偏差值

net = init(net);
net.iw{1,1}
net.b{1}

权重和偏差再次初始化：

3.4上述完整源码

%创建一个感知器
x = [0 1 0 1; 0 0 1 1];
t = [0 0 0 1];
net = perceptron;
net = configure(net,x,t);
net.iw{1,1}
net.b{1}
%训练建立的神经网络
net = train(net,x,t);
net.iw{1,1}
net.b{1}
%重新初始化权重和偏差值
net = init(net);
net.iw{1,1}
net.b{1}

四、感知器相关函数

可以当作是对上面一些列函数的补充，但是又有一些区别，这里我要讲到的是与感知器相关的函数。

一.绘制样本点函数

这里我们要用到plotov函数，该函数可以在坐标途中绘制出样本点及类别，不同类别使用不同的符号。
语法：

plotpv(X,T);

其中P为n个二维或三维的样本矩阵，T为各个样本点的类别。
例如：

%绘制样本点函数
X = [ -0.5 -0.5 +0.3 -0.1;  
      -0.5 +0.5 -0.5 +1.0];
T = [1 1 0 0];
plotpv(X,T);

返回：

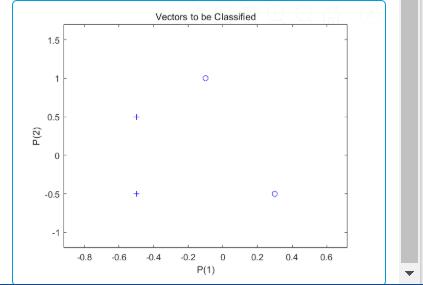
我们可以看到：点[0.5 0.5]和点[0.5 -0.5]用的”+“表示，其它两个点用的圆点表示。

二.绘制分类线综合应用

这里 PERCEPTRON 创建了一个具有单个神经元的新神经网络。然后针对数据配置网络，这样我们可以检查其初始权重和偏置值。（通常可以跳过配置步骤，因为 ADAPT 或 TRAIN 会自动完成配置。）

net = perceptron;
net = configure(net,X,T);

神经元初次尝试分类时，输入向量会被重新绘制。初始权重设置为零，因此任何输入都会生成相同的输出，而且分类线甚至不会出现在图上。别担心…我们将对它进行训练！

plotpv(X,T);
plotpc(net.IW{1},net.b{1});

此时全部代码：

返回为：

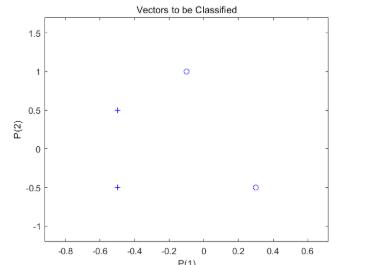
此时，输入数据和目标数据转换为顺序数据（元胞数组，其中每个列指示一个时间步）并复制三次以形成序列 XX 和 TT。ADAPT 针对序列中的每个时间步更新网络，并返回一个作为更好的分类器执行的新网络对象。
代码为：

net = perceptron;
net = configure(net,X,T);
plotpv(X,T);
plotpc(net.IW{1},net.b{1});
XX = repmat(con2seq(X),1,3);
TT = repmat(con2seq(T),1,3);
net = adapt(net,XX,TT);
plotpc(net.IW{1},net.b{1});

返回：

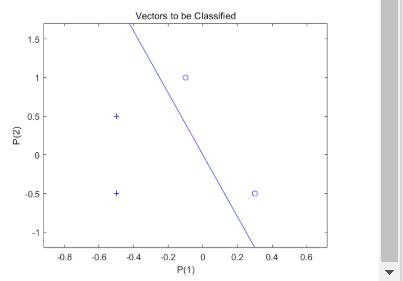
现在 SIM 用于对任何其他输入向量（如 [0.7; 1.2]）进行分类。此新点及原始训练集的绘图显示了网络的性能。为了将其与训练集区分开来，将其显示为红色。
加上这部分代码：

x = [0.7; 1.2];
y = net(x);
plotpv(x,y);
point = findobj(gca,'type','line');
point.Color = 'red';

返回：

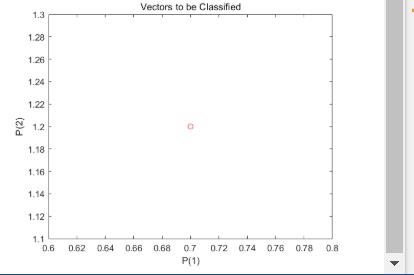
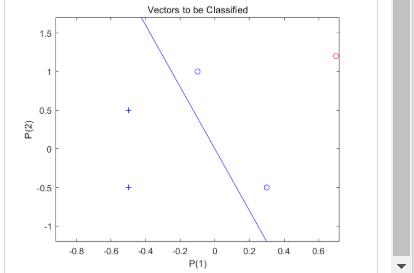
开启“hold”，以便先前的绘图不会被删除，并绘制训练集和分类线。感知器正确地将我们的新点（红色）分类为类别“零”（用圆圈表示）而不是“一”（用加号表示）。
此时最终完整源码为：


net = perceptron;
net = configure(net,X,T);
plotpv(X,T);
plotpc(net.IW{1},net.b{1});
XX = repmat(con2seq(X),1,3);
TT = repmat(con2seq(T),1,3);
net = adapt(net,XX,TT);
plotpc(net.IW{1},net.b{1});
x = [0.7; 1.2];
y = net(x);
plotpv(x,y);
point = findobj(gca,'type','line');
point.Color = 'red';
hold on;
plotpv(X,T);
plotpc(net.IW{1},net.b{1});
hold off;

三.感知器学习函数

这里我要见到的是learnp函数。感知器学习规则为调整网络的权值和偏值，使得感知平均绝对误差性能最小，以便对对网络输入向量正确分类。感知器的学习规则只能训练单层网络。
语法：

[dW,LS] = learnp(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)

其中，W权重矩阵,P为输入向量矩阵；T为目标向量;E为误差向量；Z加权输入向量，N网络输入向量,A输出向量,T层目标向量,E层误差向量,gw与性能相关的权重梯度,gA与性能相关的输出梯度,D神经元距离,dw,LS分别表示为权值和偏值变化矩阵。当然，除了P,T,E其它都可以默认为[]，但是不能为空。

举个例子，在这里，您为具有两个元素输入和三个神经元的层定义了一个随机输入 P 和误差 E。

%感知器学习函数
P = rand(2,1);
T = rand(3,1);
%为空参数不可省略
dw=learnp([],P,[],[],[],[],T,[],[],[],[],[])

返回为：

四.平均绝对误差性能函数

这里我们用到的是mae函数。感知器的学习规则是调整网络的权值和偏值，使得神经网络的平均误差和最小。
语法：

perf = mae(E,Y,X,FP)

其中，E为感知器输出误差矩阵；Y为表示感知器的输出向量;X表示感知器的权值和偏值向量。
举个例子，用mac函数求解一个神经网络的平均绝对误差：
第一步：创建并配置一个感知器，使其具有一个输入和一个神经元

net = perceptron;
net = configure(net,0,0);

给网络提供一批输入 P。通过从目标 T 中减去输出 A 来计算误差。然后计算平均绝对误差。

p = [-10 -5 0 5 10];
t = [0 0 1 1 1];
y = net(p)
e = t-y
perf = mae(e)

全部代码为：

%平均绝对值误差函数
net = perceptron;
net = configure(net,0,0);
p = [-10 -5 0 5 10];
t = [0 0 1 1 1];
y = net(p)
e = t-y
perf = mae(e)

返回：

由此可知神经网络平均绝对误差为：0.4

五、源码下载地址

https://github.com/89461561511656/matlab

六、总结

我还没写完，暂时先写到这，我不图你们的访问量，建模的每一篇文章都是精心的写了几个小时，这样的文章我只希望真的能帮助到需要看的人，希望看到此篇文章的人认真学。

以上是关于数学建模学习（30）：神经网络算法模型之感知器，详细讲解+完整代码，包教包会！的主要内容，如果未能解决你的问题，请参考以下文章

神经网络算法：单层感知器算法原理及应用

单层感知器

《神经网络与深度学习》算法伪代码汇总

数学建模MATLAB应用实战系列（106）-机器学习算法：BP神经网络（附MATLAB代码）

python之感知器-从零开始学深度学习