Python数学建模系列：规划问题之非线性规划

Posted 2021-09-10 海轰Pro

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python数学建模系列：规划问题之非线性规划相关的知识，希望对你有一定的参考价值。

文章目录

前言
往期文章
非线性规划
- 例题 - 1
- 例题 - 2
结语

前言

Hello！小伙伴！
非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

自我介绍 ଘ(੭ˊᵕˋ)੭
昵称：海轰
标签：程序猿｜C++选手｜学生
简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖…已保研。目前正在学习C++/Linux/Python
学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

初学Python 小白阶段
文章仅作为自己的学习笔记用于知识体系建立以及复习
题不在多学一题懂一题
知其然知其所以然！

往期文章

Python数学建模系列（一）：规划问题之线性规划

Python数学建模系列（二）：规划问题之整数规划

非线性规划

非线性规划可以简单分两种，目标函数为凸函数or非凸函数

凸函数的非线性规划，比如 $fun = x^2 + y^2 + xy$ ,有很多常用库完成，比如cvxpy

非凸函数的非线性规划(求极值)，可以尝试以下方法:

纯数学方法，求导求极值
神经网络、深度学习(反向传播算法中链式求导过程)
scipy. optimize. minimize

scipy.optimize.minimize(fun,x0,args=(),method=None,jac=None,hess=None,hessp=None,bounds= None,constaints=() , tol= None,Callback= None, options=None)

fun:求最小值的目标函数
args:常数值
constraints :约束条件
method:求极值方法，一 般默认。
xO:变量的初始猜测值，注意minimize是局部最优

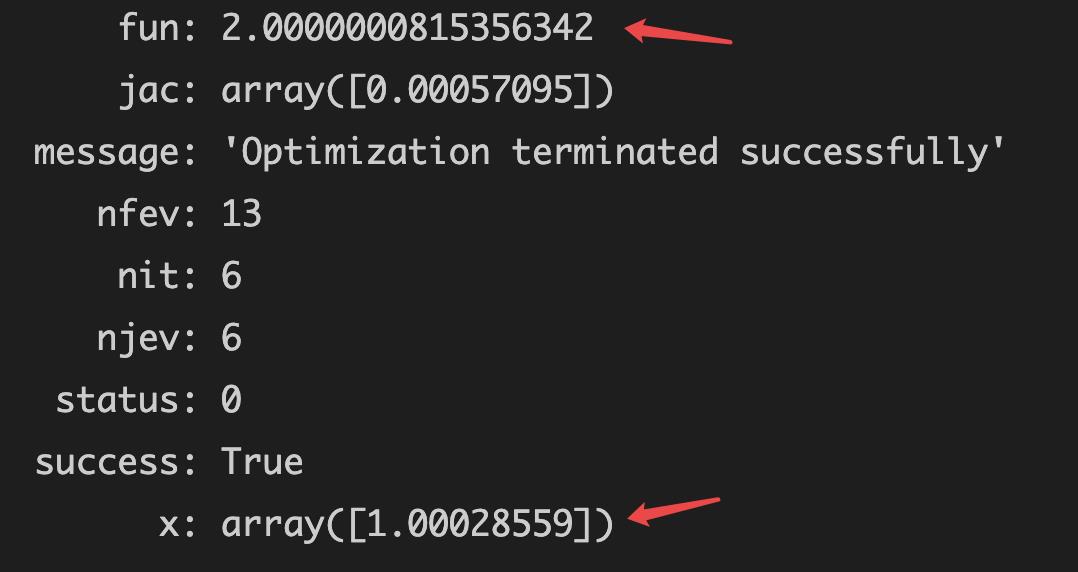
例题 - 1

计算1/x + x 的最小值

from scipy.optimize import minimize
import numpy as np

def fun(args):
    a = args
    v = lambda x:a/x[0] + x[0]
    return v

args = (1)
x0 = np.asarray((2))
res = minimize(fun(args), x0, method='SLSQP')
res

例题 - 2

计算 $2+x_1)/(1+x_2) - 3x_1 + 4x_3$ 的最小值，其中 $x_1、x_2、x_3$ 范围在0.1 到 0.9 之间

# 运行环境 Vs Code
from scipy.optimize import minimize
import numpy as np

def fun(args):
    a,b,c,d = args
    v = lambda x: (a + x[0]) / (b + x[1]) - c * x[0] + d * x[2]
    return v

def con(args):
    x1min,x1max,x2min,x2max,x3min,x3max = args
    cons = ({'type':'ineq','fun':lambda x : x[0] - x1min},\\
        {'type':'ineq','fun':lambda x:-x[0] + x1max},\\
        {'type':'ineq','fun':lambda x:x[1] - x2min},\\
        {'type':'ineq','fun':lambda x:-x[1] + x2max},\\
        {'type':'ineq','fun':lambda x:x[2] - x3min},\\
        {'type':'ineq','fun':lambda x:-x[2] + x3max})
    return cons

args = (2,1,3,4)
args1 = (0.1, 0.9,0.1, 0.9,0.1, 0.9)
cons = con(args1)

x0 = np.asarray((0.5,0.5,0.5))
res = minimize(fun(args), x0, method='SLSQP',constraints=cons)
res.fun,res.success,res.x,res.status

# 结果
(-0.773684210526435, True, array([0.9, 0.9, 0.1]), 0)