LeetCode 789. 逃脱阻碍者（贪心） / 1646. 获取生成数组中的最大值 / 787. K 站中转内最便宜的航班（有限制的最短路，重新审视迪杰斯特拉，动态规划）

Posted 2021-09-10 Zephyr丶J

789. 逃脱阻碍者

2021.8.22 每日一题

题目描述

你在进行一个简化版的吃豆人游戏。你从 [0, 0] 点开始出发，你的目的地是 target = [xtarget, ytarget] 。地图上有一些阻碍者，以数组 ghosts 给出，第 i 个阻碍者从 ghosts[i] = [xi, yi] 出发。所有输入均为 整数坐标 。

每一回合，你和阻碍者们可以同时向东，西，南，北四个方向移动，每次可以移动到距离原位置 1 个单位 的新位置。当然，也可以选择 不动 。所有动作 同时 发生。

如果你可以在任何阻碍者抓住你 之前 到达目的地（阻碍者可以采取任意行动方式），则被视为逃脱成功。如果你和阻碍者同时到达了一个位置（包括目的地）都不算是逃脱成功。

只有在你有可能成功逃脱时，输出 true ；否则，输出 false 。

示例 1：

输入：ghosts = [[1,0],[0,3]], target = [0,1]
输出：true
解释：你可以直接一步到达目的地 (0,1) ，在 (1, 0) 或者 (0, 3) 位置的阻碍者都不可能抓住你。

示例 2：

输入：ghosts = [[1,0]], target = [2,0]
输出：false
解释：你需要走到位于 (2, 0) 的目的地，但是在 (1, 0) 的阻碍者位于你和目的地之间。

示例 3：

输入：ghosts = [[2,0]], target = [1,0]
输出：false
解释：阻碍者可以和你同时达到目的地。

示例 4：

输入：ghosts = [[5,0],[-10,-2],[0,-5],[-2,-2],[-7,1]], target = [7,7]
输出：false

示例 5：

输入：ghosts = [[-1,0],[0,1],[-1,0],[0,1],[-1,0]], target = [0,0]
输出：true

提示：

1 <= ghosts.length <= 100
ghosts[i].length == 2
-10^4 <= xi, yi <= 10^4
同一位置可能有 多个阻碍者 。
target.length == 2
-10^4 <= xtarget, ytarget <= 10^4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/escape-the-ghosts
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

按这个思路，写了个代码，然后一提交，过了…惊呆我了
然后一看题解，果然是这样，这个距离叫曼哈顿距离

class Solution {
    public boolean escapeGhosts(int[][] ghosts, int[] target) {
        //因为看到同时到达目的地也算被抓住，然后想到一个很直观的思路就是，
        //如果有一个阻碍者先到达目的地，等着，那么肯定就不能成功
        //那么算距离就行了吗？
        //再想想，有没有可能阻碍者的距离大，但是还是能抓住；感觉好像不行
        int min = Math.abs(target[0]) + Math.abs(target[1]);

        int l = ghosts.length;
        for(int i = 0; i < l; i++){
            int temp = Math.abs(ghosts[i][0] - target[0]) + Math.abs(ghosts[i][1] - target[1]);
            if(temp <= min)
                return false;
        }
        return true;

    }
}

1646. 获取生成数组中的最大值

2021.8.23 每日一题

题目描述

给你一个整数 n 。按下述规则生成一个长度为 n + 1 的数组 nums ：

nums[0] = 0
nums[1] = 1
当 2 <= 2 * i <= n 时，nums[2 * i] = nums[i]
当 2 <= 2 * i + 1 <= n 时，nums[2 * i + 1] = nums[i] + nums[i + 1]
返回生成数组 nums 中的 最大 值。

示例 1：

输入：n = 7
输出：3
解释：根据规则：
nums[0] = 0
nums[1] = 1
nums[(1 * 2) = 2] = nums[1] = 1
nums[(1 * 2) + 1 = 3] = nums[1] + nums[2] = 1 + 1 = 2
nums[(2 * 2) = 4] = nums[2] = 1
nums[(2 * 2) + 1 = 5] = nums[2] + nums[3] = 1 + 2 = 3
nums[(3 * 2) = 6] = nums[3] = 2
nums[(3 * 2) + 1 = 7] = nums[3] + nums[4] = 2 + 1 = 3
因此，nums = [0,1,1,2,1,3,2,3]，最大值 3

示例 2：

输入：n = 2
输出：1
解释：根据规则，nums[0]、nums[1] 和 nums[2] 之中的最大值是 1

示例 3：

输入：n = 3
输出：2
解释：根据规则，nums[0]、nums[1]、nums[2] 和 nums[3] 之中的最大值是 2

提示：

0 <= n <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/get-maximum-in-generated-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

class Solution {
    public int getMaximumGenerated(int n) {
        //模拟
        if(n == 0)
            return 0;
        int[] nums = new int[n + 1];
        nums[0] = 0;
        nums[1] = 1;
        int max = 1;
        for(int i = 2; i <= n; i++){
            if(i % 2 == 0){
                nums[i] = nums[i / 2];
            }else{
                nums[i] = nums[i / 2] + nums[i / 2 + 1]; 
            }
            max = Math.max(max, nums[i]);
        }
        return max;
    }
}

787. K 站中转内最便宜的航班

2021.8.24 每日一题

题目描述

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 toi 抵达 pricei。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的 价格最便宜 ，并返回该价格。 如果不存在这样的路线，则输出 -1。

示例 1：

输入:
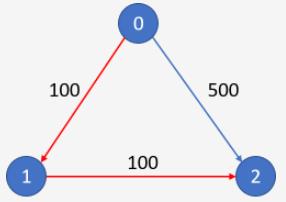
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下

从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。

示例 2：

输入:

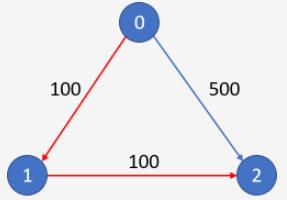
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释:
城市航班图如下

从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。

提示：

1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= fromi, toi < n
fromi != toi
1 <= pricei <= 10^4
航班没有重复，且不存在自环
0 <= src, dst, k < n
src != dst

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cheapest-flights-within-k-stops
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

又是最短路问题，最近做了好多这种题了，应该还能用迪杰斯特拉，用一个维度来表示中转的站数，如果大于k了，那么就跳过这条路线，如果达到这个点了，就返回当前花费，如果都不行，就返回-1

我是没想到会超时，那个输入也就13个点，这就超时了？？？想到问题了，应该是有环
那么应该怎么办呢，

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        //应该还能用迪杰斯特拉，用一个维度来表示中转的站数，
        //如果大于k了，那么就跳过这条路线，如果达到这个点了，就返回当前花费，如果都不行，就返回-1

        int l = flights.length;

        //先存图
        List<int[]>[] map = new List[n];
        for(int i = 0; i < n; i++){
            map[i] = new ArrayList<int[]>();
        }
        for(int i = 0; i < l; i++){
            int[] f = flights[i];
            List<int[]> list = map[f[0]];
            list.add(new int[]{f[1], f[2]});;
        }

        //三个参数，第一个达到的点，第二个花费，第三个中转的站数
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[1] - b[1]));
        //初始位置，花费为0，中转个数为-1
        pq.offer(new int[]{src, 0, -1});
        while(!pq.isEmpty()){
            //取出当前位置
            int[] curr = pq.poll();
            //如果小于等于k了，并且到达了终点
            if(curr[2] <= k && curr[0] == dst){
                return curr[1];
            }
            //如果中转站数超过了，直接跳过
            if(curr[2] >= k)
                continue;
            //取出当前位置能直接相连的点
            List<int[]> list = map[curr[0]];
            for(int[] pos : list){
                pq.offer(new int[]{pos[0], pos[1] + curr[1], curr[2] + 1});
            }
        }
        return -1;
    }
}

如果有环的话，每次到达该节点，花费就会不断增加，所以用一个数组记录每个节点的花费，如果到达某个节点时，花费大于当前cost[i]，那么这个节点就不加入队列了
但是这样还会造成一个问题，因为这个题中，还有中转次数的限制；如果刚刚到达这个点的最小花费中转次数很多，导致不能达到目标了；而花费多的中转次数少，也是可行的。所以还要设置一个数组，表示达到这个点中转了多少次，如果中转次数小，还是要入队列
这样，如果存在环的话，首先花费是一个筛选条件，其次，中转次数又是一个条件；这样，肯定能遍历到环外的点

但是呢，我又想了一下，刚刚没有这些筛选条件的时候，在环中走，也是会消耗中转次数的，如果中转次数等于0，也是会跳出环去走别的路线的。刚刚k也不是很大，为什么呢？想不太通
这种就是相当于剪枝了，去除了一些情况

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        //应该还能用迪杰斯特拉，用一个维度来表示中转的站数，
        //如果大于k了，那么就跳过这条路线，如果达到这个点了，就返回当前花费，如果都不行，就返回-1

        int l = flights.length;

        //先存图
        List<int[]>[] map = new List[n];
        for(int i = 0; i < n; i++){
            map[i] = new ArrayList<int[]>();
        }
        for(int i = 0; i < l; i++){
            int[] f = flights[i];
            List<int[]> list = map[f[0]];
            list.add(new int[]{f[1], f[2]});;
        }

        int[] costs = new int[n];
        int[] station = new int[n];
        Arrays.fill(costs, Integer.MAX_VALUE);
        //三个参数，第一个达到的点，第二个花费，第三个中转的站数
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[1] - b[1]));
        //初始位置，花费为0，中转个数为-1
        pq.offer(new int[]{src, 0, -1});
        while(!pq.isEmpty()){
            //取出当前位置
            int[] curr = pq.poll();
            //如果小于等于k了，并且到达了终点
            if(curr[2] <= k && curr[0] == dst){
                return curr[1];
            }
            //如果中转站数超过了，直接跳过
            if(curr[2] >= k)
                continue;
            //取出当前位置能直接相连的点
            List<int[]> list = map[curr[0]];
            for(int[] pos : list){
                int cost = costs[pos[0]];
                //如果当前花费小的话，那么就入队列
                if(curr[1] + pos[1] < cost){
                    costs[pos[0]] = curr[1] + pos[1];
                    pq.offer(new int[]{pos[0], pos[1] + curr[1], curr[2] + 1});
                    station[pos[0]] = curr[2] + 1;
                //虽然花费多，但是如果当前中转站数小的话，也得入队列
                }else if(curr[2] < station[pos[0]]){
                    pq.offer(new int[]{pos[0], pos[1] + curr[1], curr[2] + 1});
                }
            }
        }
        return -1;
    }
}

再来看主流写法，动态规划：

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        //再写动规吧
        //dp[i][j]表示经过i个站点，到达j位置的最小花费
        int l = flights.length;
        
        //中转k次，也就是经过了k+1个站（除去起始站）
        int[][] dp = new int[k + 2][n];
        for(int i = 0; i < k + 2; i++){
            Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
        }
        dp[0][src] = 0;

        for(int p = 1; p < k + 2; p++){
            //遍历所有航班，这里为什么不和平时一样遍历第二维呢，因为第二维不是从0开始的
            //当然也可以遍历起始位置和结束位置，也就是加里面两层循环，但是麻烦了
            for(int[] f : flights){
                int s = f[0], t = f[1], cost = f[2];
                dp[p][t] = Math.min(dp[p][t], dp[p - 1][s] + cost); 
            }
        }
        int res = Integer.MAX_VALUE / 2;
        for(int i = 1; i < k + 2; i++){
            res = Math.min(res, dp[i][dst]);
        }
        return res == Integer.MAX_VALUE / 2 ? -1 : res;
    }
}

学习一下克隆的用法

class Solution {
    int N = 110, INF = 0x3f3f3f3f;
    int[] dist = new int[N];
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        Arrays.fill(dist, INF);
        dist[src] = 0;
        for (int limit = 0; limit < k + 1; limit++) {
            int[] clone = dist.clone();
            for (int[] f : flights) {
                int x = f[0], y = f[1], w = f[2];
                dist[y] = Math.min(dist[y], clone[x] + w);
            }
        }
        return dist[dst] > INF / 2 ? -1 : dist[dst];
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/cheapest-flights-within-k-stops/solution/gong-shui-san-xie-xiang-jie-bellman-ford-dc94/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

感觉这个题最应该想到的是bfs，因为给定中转次数，相当于是层层扩展，然后记录终点的最小花费；花费多了，就不要扩展了

在回看最近做的迪杰斯特拉，为什么没有出现这个题中的环的问题呢？
先看了1928，前几次周赛的题，这个问题中很明显还是会有环的出现，但是这个题中也是有一个最大时间的的限制，所以也可以，当时写的时候，这里有一个数组记录了在某个时间到达某个点，花费的费用，如果大于这个费用，那么就跳过了。这个处理和今天这个题中的处理方式是一样的，所以今天这个题中也可以改成一个二维数组记录当前状态，经过k次到达某一站花费的费用
这周双周赛的题1976，同样也会有这种问题，而同样的，也是给出了时间限制

那重新看一下迪杰斯特拉，它的应用场景是有向无环图；而在无向图中，要找最短路的话，可以用一个vis[]数组记录已经走过的点，避免重复遍历
而在这种有限制的最短路问题中，是不是也能用vis数组来记录走过的点呢，显然是不太行的，因为并不是要找一条路径。那么应该怎么做呢，就是利用限制条件，并且记录到达当前点的时间（费用等，看题目条件），如果已经超过了记录的时间（…），那么说明可能是存在环了，那么就跳过本次循环。该不该直接跳过还是看条件。
总之，再次用迪杰斯特拉超时的时候，要想到怎么剪枝

而这个题的动态规划方法，也是记录到达一个点，经过k站的最小花费。可以从前向后，也可以从后向前。应该是算简单的思路了，写起来也比迪杰斯特拉简单。再碰到要会写！！！！！