❤️ 互联网大厂面试高频算法题汇总 ❤️ —— ❤️ 二分专场 ❤️

Posted 林深时不见鹿

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️ 互联网大厂面试高频算法题汇总 ❤️ —— ❤️ 二分专场 ❤️相关的知识，希望对你有一定的参考价值。

文章目录

1、前言

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法，可以在数据规模的对数时间复杂度内完成查找。二分查找可以应用于数组，是因为数组具有有随机访问的特点，并且数组是有序的。二分查找体现的数学思想是「减而治之」，可以通过当前看到的中间元素的特点推测它两侧元素的性质，以达到缩减问题规模的效果。

二分查找也是面试中经常考到的问题，虽然它的思想很简单，但写好二分查找算法并不是一件容易的事情。因此我汇总了近期互联网大厂面试的高频二分题目，数据来源于CodeTop ，题解来源于我的LeetCode高频面试题专栏，7道高频二分题详解帮助面试者更有针对性地准备面试中的二分算法题。

2、题目汇总

题目难度最近考察时间频率掌握程度
LeetCode 33. 搜索旋转排序数组中等2021-08-1965⭐⭐⭐
LeetCode 704. 二分查找容易2021-08-2047⭐⭐⭐
LeetCode 69. x 的平方根容易2021-08-2337⭐⭐⭐
LeetCode 4. 寻找两个正序数组的中位数困难2021-08-2127⭐⭐⭐
LeetCode 153. 寻找旋转排序数组中的最小值中等2021-08-1422⭐⭐⭐
LeetCode 162. 寻找峰值中等2021-08-1720⭐⭐⭐
LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置中等2021-08-1218⭐⭐⭐

3、二分模板

版本1

当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1，计算mid时不需要加1。

C++/java代码模板：

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = (l + r)/2;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

版本2

当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid，此时为了防止死循环，计算mid时需要加1。

C++/java 代码模板：

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = ( l + r + 1 ) /2;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

代码模板链接： https://www.acwing.com/blog/content/31/

4、二分流程

  • 1、确定二分的区间[l,r]，一般都是l = 0, r = nums.size() - 1。
  • 2、编写二分的代码模板。
  • 3、确定判断条件check，可以通过画图来判断当满足check时，区间该如何更新。

5、二分高频题详解

5.1、LeetCode 33. 搜索旋转排序数组

题目：

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7]在下标3 处经旋转后可能变为[4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums和一个整数 target ，如果nums中存在这个目标值target ，则返回它的下标，否则返回 -1。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

  • 1 <= nums.length <= 5000
  • -10^4 <= nums[i] <= 10^4
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums在预先未知的某个下标上进行了旋转
  • -10^4 <= target <= 10^4

思路

(二分) O ( l o g n ) O(logn) O(logn)

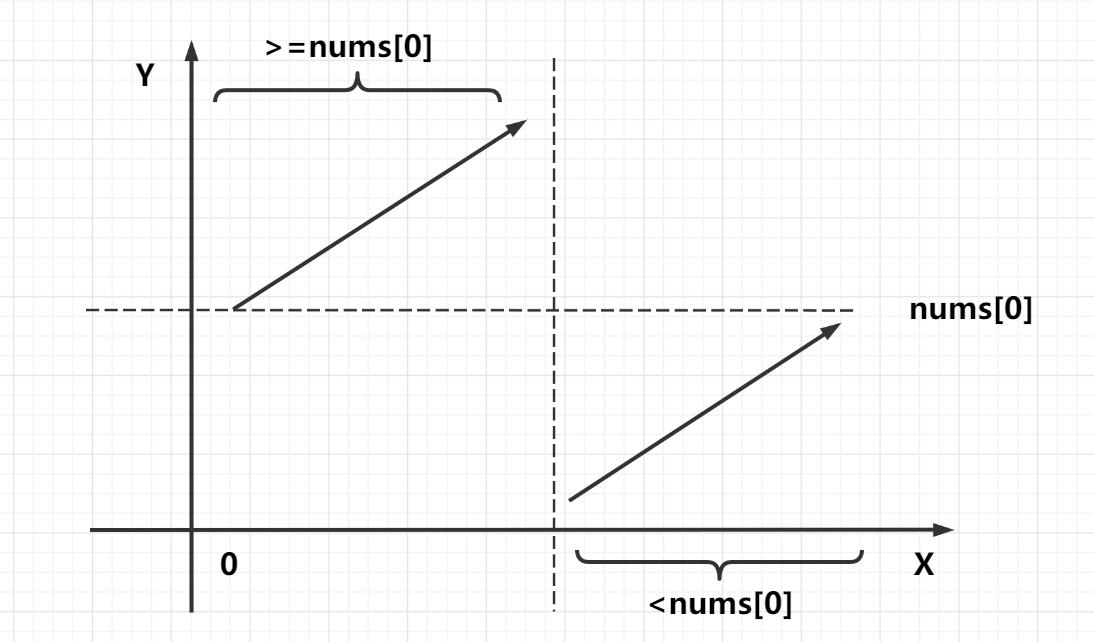
1、先找到旋转点，在旋转点左边的点都比nums[0]大，右边的点都比nums[0]小，因此可以用二分找到该点

  • 当nums[mid] >= nums[0]时，往右边区域找，l = mid。

  • 当nums[mid] < nums[0]时，往左边区域找，r = mid - 1。

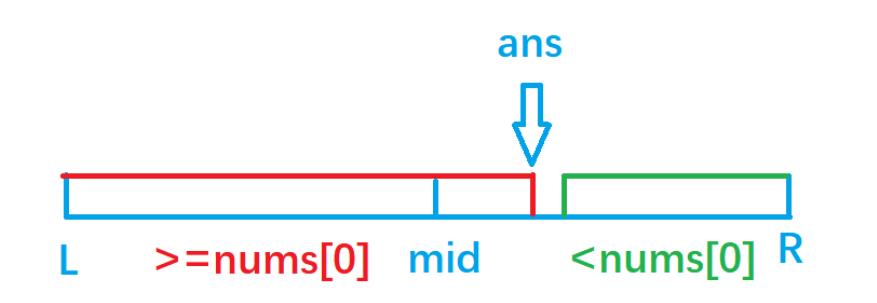
2、找到旋转点l后，可以知道[0,l - 1],[l,n - 1]是两个有序数组，判断出target的值在哪个有序数组中，确定好二分的区间[l,r]

3、在[l,r]区间中，由于该区域也具有单调性，通过二分找到该值的位置

  • 当nums[mid] >= target时，往左边区域找，r = mid。

  • 当nums[mid] < target时， 往右边区域找, l = mid + 1。

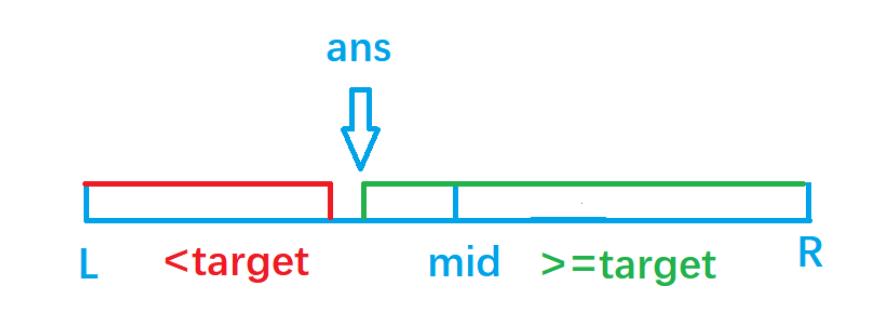
4、若最后找到的元素nums[r] != target，则表示不存在该数，返回-1，否则返回该数值

c++代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
       if(nums.empty()) return -1; 
       //先二分转折点 二分>=nums[0]的最右边
       int l = 0, r = nums.size() - 1;
       while( l < r)
       {
           int mid = (l + r + 1)/2;
           if(nums[mid] >= nums[0]) l = mid;
           else r = mid - 1;
       }
       if(target >= nums[0]) l = 0;  //target在左半边区域
       else l = r + 1, r = nums.size() - 1; //target在右半边区域
       while( l < r)
       {
           int mid = ( l + r)/2;
           if( nums[mid] >= target) r = mid;
           else l = mid + 1;
       }
       if(nums[r] == target) return r;//二分的while循环的结束条件是l>=r，所以在循环结束时l有可能会大于r，此时就可能导致越界，基本上二分问题优先取r都不会翻车。
       return -1;
    }
};

java代码

class Solution {
    public int search(int[] nums, int target) {
        if(nums.length == 0) return -1; 
       //先二分转折点 二分>=nums[0]的最右边
       int l = 0, r = nums.length - 1;
       while( l < r)
       {
           int mid = (l + r + 1)/2;
           if(nums[mid] >= nums[0]) l = mid;
           else r = mid - 1;
       }
       if(target >= nums[0]) l = 0;  //target在左半边区域
       else
       {
           l = r + 1;
           r = nums.length - 1; //target在右半边区域
       } 
       while( l < r)
       {
           int mid = ( l + r)/2;
           if( nums[mid] >= target) r = mid;
           else l = mid + 1;
       }
       if(nums[r] == target) return r;//二分的while循环的结束条件是l>=r，所以在循环结束时l有可能会大于r，此时就可能导致越界，基本上二分问题优先取r都不会翻车。
       return -1;
    }
}

5.2、LeetCode 704. 二分查找

题目

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

  • 你可以假设 nums中的所有元素是不重复的。
  • n 将在 [1, 10000]之间。
  • nums 的每个元素都将在 [-9999, 9999]之间。

思路

(二分) O ( l o g n ) O(logn) O(logn)

1、在[l,r]区间中，nums[i]数组具有单调性，因此可以通过二分>=target的最左边界找到该值的位置

  • 当nums[mid] >= target时，往左边区域找， r = mid
  • 当nums[mid] < target时，往右边区域找，l = mid + 1

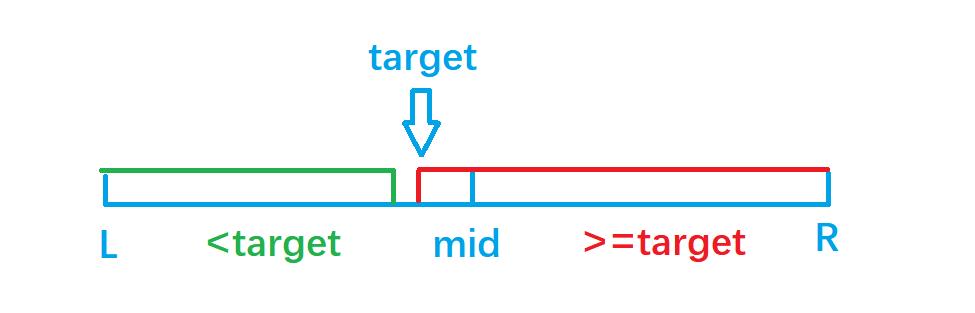
2、若最后找到的元素nums[r] != target，则表示不存在该数，返回-1，否则返回数值r

c++代码

class Solution {
public:
    int search(vector<int>& nums, int target) {
      if(!nums.size()) return -1;
      int  l = 0, r =nums.size() - 1;
      while(l < r)   //二分>=x的最左边界
      {
          int mid = (l + r) / 2;
          if(nums[mid] >= target) r = mid;
          else l = mid + 1;
      }
      if(nums[r] == target) return r;
      else return -1;
    }
};

java代码

class Solution {
    public int search(int[] nums, int target) {
     if(nums.length == 0) return -1;
      int  l = 0, r =nums.length- 1;
      while(l < r) //二分>=x的最左边界
      {
          int mid = (l + r) / 2;
          if(nums[mid] >= target) r = mid;
          else l = mid + 1;
      }
      if(nums[r] == target) return r;
      else return -1;
    }
}

5.3、LeetCode 69. x 的平方根

题目

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例2：

输入: 8
输出: 2

说明:

  • 8的平方根是 2.82842…,
  • 由于返回类型是整数，小数部分将被舍去。

思路

(二分) O ( l o g x ) O(logx) O(logx)

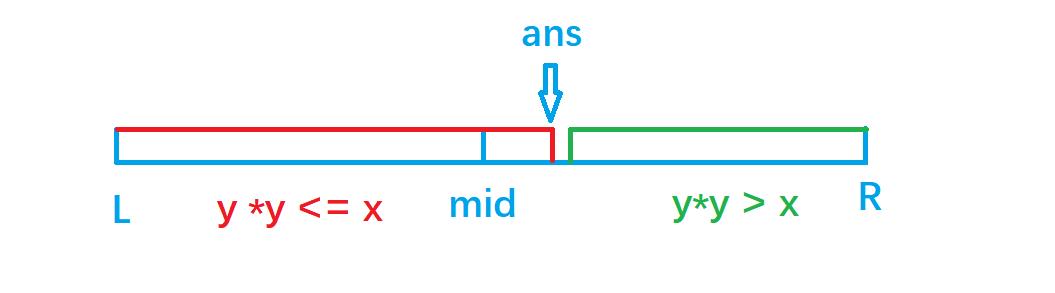
我们二分出最大的 y 2 < = x y^2 <= x y2<=x ,那么y就是答案

过程

  • 1、我们从l = 0，r = x开始，先让mid = (l + r + 1)/2
  • 2、如果mid * mid <= x ，则往右边查找，即l = mid，否则往左边查找，即r = mid - 1。

图示过程

时间复杂度 O ( l o g x ) O(logx) O(logx)

注意点

  • 1、r最大可以取INT_MAX再加上1就会超出int范围，因此我们将其写成l + r +1ll强转为long long类型，再/2就不会出现越界情况了。
  • 2、mid * mid可能会超出int的范围，因此判断条件写成 if( mid <= x/mid )。

c++代码

class Solution {
public:
    int mySqrt(int x) {
        int l = 0 , r = x;
        while(l < r)
        {
            int  mid = (l + r + 1ll)/2;
            if(mid <= x/mid) l = mid;
            else r = mid - 1;
        }
        return r;
    }
};

java代码

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x;
        while(l < r)
        {
            int mid = (int)(l + r + 1L >> 1);
            if(mid <= x / mid) l = mid;
            else r = mid - 1;
        }
        return l;
    }
}

5.4、LeetCode 4. 寻找两个正序数组的中位数

题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

进阶： 你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

思路

(递归，二分) O ( l o g ( n + m ) ) O(log(n+m)) O(log(n+m))

找出两个正序数组的中位数等价于找出两个正序数组中的第k小数。如果两个数组的大小分别为n和m ，那么第 k = (n + m)/2 小数就是我们要求的中位数。

如何寻找第k小的元素？

过程如下：

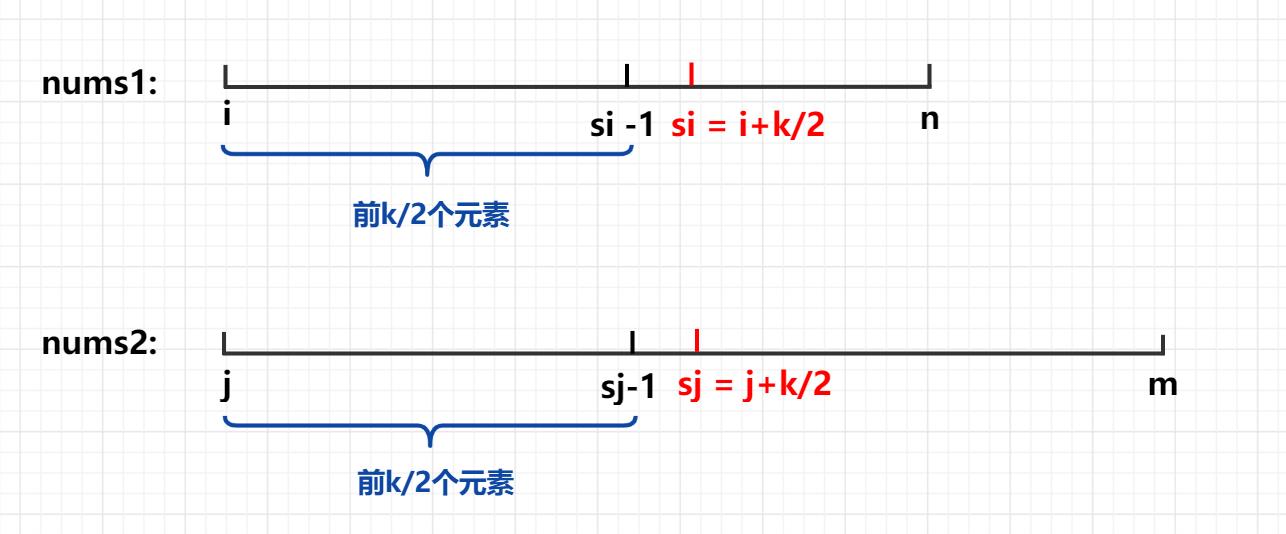
1、考虑一般情况，我们在 nums1和nums2数组中各取前k/2个元素

or_FFFFFF,t_70,g_se,x_16#pic_center)

我们默认nums1数组比nums2数组的有效长度小 。nums1数组的有效长度从i开始，nums2数组的有效长度从j开始，其中[i,si - 1]是nums1数组的前k / 2个元素，[j, sj - 1]是nums2数组的前k / 2个元素。

2、接下来我们去比较nums1[si - 1]和nums2[sj - 1]的大小。

  • 如果nums1[si - 1] > nums2[sj - 1] ，则说明 nums1 中取的元素过多，nums2 中取的元素过少。因此nums2 中的前 k/2个元素一定都小于等于第 k 小数，即nums2[j,sj-1]中元素。我们可以舍去这部分元素，在剩下的区间内去找第k - k / 2小的元素，也就是说第k小一定在[i,n]与[sj,m]中。
  • 如果nums1[si - 1] <= nums2[sj - 1]，同理可说明nums2中的前 k/2个元素一定都小于等于第 k 小数，即nums1[i,si-1]中元素。我们可以舍去这部分元素，在剩下的区间内去找第k - k / 2小的元素，也就是说第k小一定在[si,n]与[j,m]中。

3、递归过程2，每次可将问题的规模减少一半，最后剩下的一个数就是我们要找的第k小数。

递归边界：

  • 当nums1数组为空时，我们直接返回nums2数组的第k小数。
  • 当k == 1时，且两个数组均不为空，我们返回两个数组首元素的最小值，即min(nums1[i], nums2[j])。

奇偶分析：

  • 当两个数组元素个数的总和total为偶数时，找到第total / 2小left和第total / 2 + 1小right，结果是(left + right / 2.0)。

  • 当total为奇数时，找到第total / 2 + 1小，即为结果。

时间复杂度分析： k = ( m + n ) / 2 k=(m+n)/2 k=(m+n)/2，且每次递归 k k k 的规模都减少一半，因此时间复杂度是 O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)).

这道题是二分类型的题目，但使用递归解法会更通俗易懂，每次递归 k k k 的规模都减少一半，也是二分的思想体现。

c++代码

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int tot = nums1.size() + nums2.size();
        if (tot % 2 == 0) {
            int left = find(nums1, 0, nums2, 0, tot / 2);
            int right = find(nums1, 0, nums2, 0, tot / 2 + 1);
            return (left + right) / 2.0;
        } else {
            return find(nums1, 0, nums2, 0, tot / 2 + 1);
        }
    }

    int find(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
        if (nums1.size() - i > nums2.size() - j) return find(nums2, j, nums1, i, k);
        if (k == 1) {
            if (nums1.size() == i) return nums2[j];
            else return min(nums1[i], nums2[j]);
        }
        if (nums1.size() == i) return nums2[j + k - 1];
        int si = min((int)nums1.size(), i + k / 2), sj = j + k - k / 2;
        if (nums1[si - 1] > nums2[sj - 1])
            return find(nums1, i, nums2, sj, k - (sj - j));
        else
            return find(nums1, si, nums2, j, k - (si - i));
    }
};

java代码

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int total = nums1.length + nums2.length;
        if(total 
以上是关于❤️ 互联网大厂面试高频算法题汇总 ❤️ —— ❤️ 二分专场  ❤️的主要内容，如果未能解决你的问题，请参考以下文章
 

 Redis高频面试题汇总（2021最新版）


 ❤️思维导图整理大厂面试高频数组: 两万字详解各种数组求和(建议收藏)❤️


 ❤️思维导图整理大厂面试高频数组: 两万字详解各种数组求和(建议收藏)❤️


 ❤️导图整理大厂面试高频数组8: 移除元素的双指针优化, 力扣27❤️


 ❤️思维导图整理大厂面试高频数组12: 4种方法彻底解决接雨水问题, 力扣42❤️


 ❤️思维导图整理大厂面试高频数组12: 4种方法彻底解决接雨水问题, 力扣42❤️