python实现高级算法与数据结构:如何实现百度的竞价排名1

Posted 2021-09-09 tyler_download

百度的竞价排名机制被严重诟病，但如果没有这个设计，百度也不会发展成BAT三大巨头之一，虽然现在形势不如以前，但是依然靠这项机制挣得盆满钵满，我们不在道德上对其进行批判，而是从技术上看看，竞价排名是如何实现的。

竞价排名其实就是根据客户付费的多少来决定客户网页的优先级，然后在显示时依次进行展示。假设你在百度里输入一个关键词，大多数情况下你只会浏览首页给出的链接，因此首页位置资源极其珍贵。通常情况下，首页给出的也就是十几个链接左右，但是一个关键词极有可能对应几十万，甚至是几百万个网页，百度是如何将这十几个网页在几秒时间内从几百万个网页中抽取出来呢，而且网页的权重会根据付费情况进行动态调整，当某个广告主增加或减少预算后，其对应主页能迅速在几百万个含有给定关键词的网页中快速调整其排位，那么百度是如何做到排名能更加竞价迅速调整的呢。

我们把问题抽象一下，用n 表示关键词对应的网页数，n可能高达几十上百万，k表示排在首页的链接，这些链接会根据付费情况迅速进行动态调整。每个网页对应一个权重值，于是n个网页就对应含有n个元素的数组，问题就回归为如何在含有n个元素的数组中快速找到前k大的元素，而且这k个元素还能快速应对权重的变化，假设当某个网页的权重一下子提升到前k的范围内，那么它必须要迅速被筛选进入这前k个元素。

最简单的做法自然是将n个网页根据权重进行排序，然后取出最后k个，排序的算法复杂度是O(n*lg(n))，如果排好序后，当某个网页的权重发生变化后，就得遍历整个数组才能确定其新位置，几百万个元素执行快速排序时间消耗依然很大，很难在两秒内将结果展现出来，但是时间长了又会影响体验，而且网页的排名会经常变动，没变动一次就得遍历全部相关网页一次，那么系统的压力会非常承重，有没有快速又迅捷的应对方法呢。

要实现这个需求，我们需要先了解一个数据结构叫“堆”，堆是一种类似二叉树的结构，它具有如下特性：
1，每个节点最多含有两个子节点。
2，堆，如果是完全的，和左倾的，那意味着，当堆的高度为H时，每个叶子节点对应的高度就是H或H-1。左倾意味着任何一个节点的右子树高度一定小于等于左子树高度。
3，对任何一个子树的根节点而言，其值一定是所有节点中的最小值或是最大值，如果是最小值它就称为小堆，如果根节点是最大值那么就称为大堆。

堆能够支持以下操作：
top() -> 把根节点元素取出， peek()->只读取根节点数值，不把它取出，insert(element, priority)->把节点根据其权重插入堆;remove(elemt)->把给定节点从堆中去除，update(element, priority)->修改某个节点的权重值。

如果有n个元素，那么把他们构建成堆所需时间为O(n*lg(n))，而作用在堆上的操作，例如top,peek,都只需要O(1)复杂度，insert, update, remove等操作所需要的复杂度为O(lg(n))。对于堆的基本原理，我在如下链接对应的数据结构和算法课程里说的非常清楚：课程链接

堆在结构上看可以形成二叉树，但在实现上可以直接在数组上构建，而二叉树上父节点和子节点的关系可以通过数组中的下标来描述。在堆中，父节点和子节点的关系为：如果父节点在数组中的下标为i, 那么它的左孩子对应下标为2*i+1,右孩子下标为2*(i+1)，如果这些下标数值超出了数值长度，那么该节点就没有左孩子或右孩子。给定一个节点下标为i,那么其父节点对应下标为(i - 1) / 2，我们使用python实现算法，因此代码如下:

def  left_child(idx : int) -> int:
    if idx < 0:
        raise ValueError
    return (2 * idx) + 1

def  right_child(idx : int) -> int:
    if idx < 0:
        raise ValueError
    return 2 * (idx + 1)

def  parent(idx : int) -> int:
    if idx < 0:
        raise ValueError
    if idx == 0:
        return 0
    return int((idx- 1) / 2)

我们接下来定义节点的结构，为了简单起见，节点只包含两种信息，分别为一个字符串和一个数值，其定义如下：
···
class Element:
def init(self, content : str, priority : int) :
self.__content = content
self.__priority = priority
@property
def content(self) -> str:
return self.__content
@content.setter
def content(self, content : str):
self.__content = content
@property
def priority(self):
return self.__priority
@priority.setter
def priority(self, priority : int) :
self.__priority = priority
def repr(self):
return “Element(’{}’, {})”.format(self.__content, self.__priority)
···
堆的构建关键在于节点的插入，假设我们已经有了一个满足条件的堆结构，如果我们在堆对应的数组末尾添加一个元素，那么堆的性质就有可能被破坏，如下图所示：

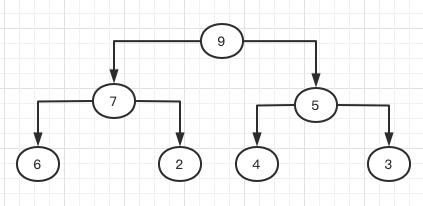
它对应的数组为9,7,5,6,2,4,3。现在我们给数组末尾添加一个元素8，那么根据前面描述的父节点和子节点的坐标关系，8加入到末尾后会成为节点6的左子节点，但从上图看，我们使用的是大堆，树的根节点值一定要大于其左右子数所有节点，但是8加入后，其父节点为6，这就违背了堆的性质，如下图所示：

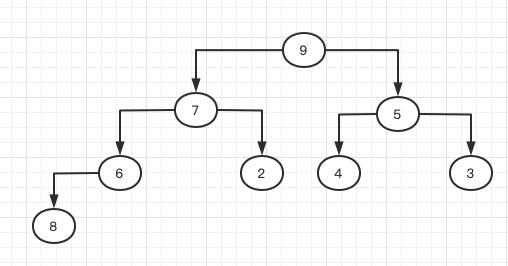
这样的话我就得调整元素的父子关系使得它满足大堆的性质。我们先从违背大堆原则的子树开始调整，由于8比6大，因此我们调整其位置，将8放到6的位置，6放到8的位置，于是节点6变成节点8的左子节点：

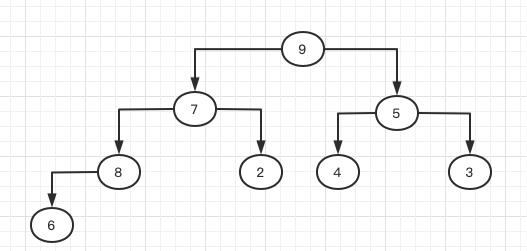
这样调整后，堆的性质还没有得到满足，因为此时节点8的父节点是7，它的值小于8，因此我们需要继续调整，将7与8的位置互换：

到这一步堆的性质也就满足了。由此堆里插入新元素时，其步骤是先将元素加入数组末尾，然后通过调整父子关系的方式让元素之间的父子关系逐渐满足堆的要求。由于当数组元素为n时，堆的高度为O(lg(n))，因此堆的元素插入复杂度就是O(lg(n))。我们看看相应代码实现：

import copy
import copy
def  copy_element( element_copyed : Element) -> Element:
    return copy.deepcopy(element_copyed)


def  bubble_up(elements : [Element], idx : int) :
    if idx < 0 or idx >= len(elements):
        raise ValueError

    current : Element = Element("", -1) 
    elements_cnt : int = len(elements) - 1
   current = copy_element(elements[elements_cnt])#1，先将插入的元素缓存起来

    while idx > 0: #2，当前节点是否为根节点
        parent_idx : int = parent(idx)
        if elements[parent_idx].priority < current.priority: #3 父节点值小于插入元素数值，它就需要调整
            elements[idx] = copy_element(elements[parent_idx]) #4 将父节点转移到子节点
            idx = parent_idx  #5将当前元素下标转变为父节点对应下标
        else:
            break
    elements[idx] = copy_element(current)#5

我们看看上面代码的逻辑，首先原来的大堆对应数组元素为：9，7，5，6，2，4，3.现在我们在末尾加入元素8，由此数组变成：9，7，5，6，2，4，3，8.根据#1，我们首先将插入末尾的元素8缓存起来，对应代码中的current变量。

变量idx对应当前要调整的元素下标，一开始其值为新加入数组元素8对应下标，因此就是7，其对应的父节点下标为3，对应元素6，根据#3，由于其数值小于插入节点数值，因此它需要调整，我们将它挪到idx对应的位置，此时idx的值位7，于是挪动后数组变成：9，7，5，6，2，4，3，6，虽然最后一个元素8被6所覆盖，但是在#1处我们已经缓存了元素8，因此这次覆盖没有问题，根据#5, idx 的值变成3，它对于父节点的值为1，也就是数值7。

紧接着循环再次执行语句#3,此时idx对应值位7，它比current对应的值，也就插入元素值8要小，于是进入到#3下面的语句，先执行#4, 它把数值7覆盖到idx执行的元素，也就是元素6，执行#4后数组变成：9，7，5，7，2，4, 3，6。然后#5将idx指向当前节点对应下标。再次进入循环体后，#3所对应的判断条件不成立，于是执行break语句结束循环，最后执行语句#5，它把current对应的值赋值给idx对应的元素，由于此时idx对应的元素为1，也就是数组中第一个元素7，于是语句#5将current对应的值赋值给它，执行后数组为:9,8,5,7,2,4,3,6,此时它对于上图所示的堆结构，我们将当前实现代码执行起来验证一下：

elements = [Element("a", 9), Element("b", 7), Element("c", 5),
            Element("d", 6), Element("e", 2), Element("f", 4), Element("g", 3),
            Element("h", 8)
            ]

bubble_up(elements, len(elements) - 1)
print("big heap: ", elements)

上面代码执行后输出结果如下：

big heap:  [Element('a', 9), Element('h', 8), Element('c', 5), Element('b', 7), Element('e', 2), Element('f', 4), Element('g', 3), Element('d', 6)]

从输出上看，我们调整堆元素的结果是正确的。另一个需要实现的是bubble_up的对称函数叫push_down，bubble_up是叶子节点值变大后需要与父节点进行转换，那么当父节点的值变小后，我们需要将它与子节点调整，把它压下去，让子节点调上来，例如下面所示的情况我们就需要把父节点往下压：

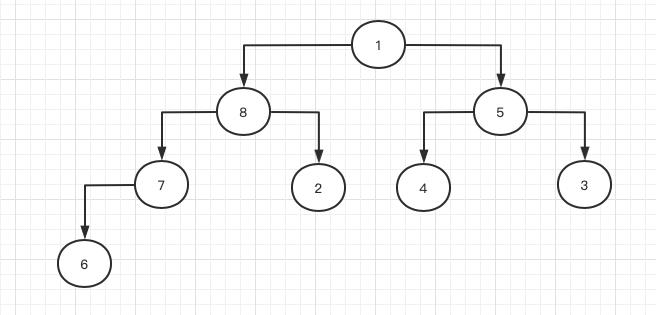
首先要找出子节点中数值最大的那个，将父节点与其进行调换。在上图中，元素1最大的子节点就是左孩子8，于是1压到8的位置，8调整到1的位置。按照相同原则继续把节点1往下压：

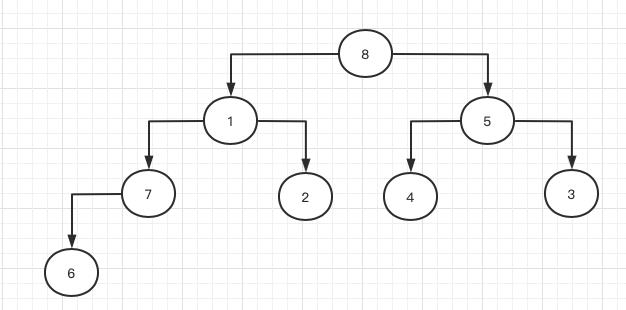
此时节点1的最大子节点还是左孩子，于是它继续往下压，左孩子7往上调，如此一直到节点1被压入到叶子节点位置：

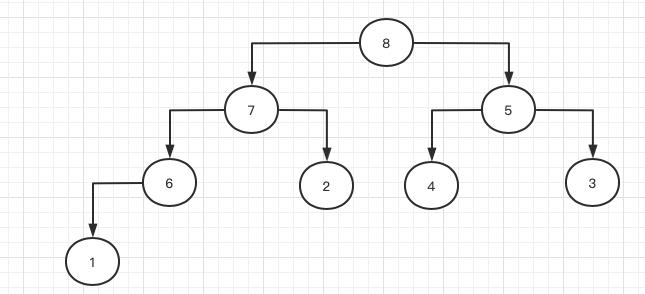
由此我们得到相应实现如下：

def  first_leave_index(elements : [Element]) -> int : #位于数组一半以后的元素没有叶子节点
    return int((len(elements) - 2) / 2) + 1

def  highest_priority_child(elements : [Element], current_idx : int) -> (Element, int):
    '''
    从左右孩子中找到优先级最大那个
    '''
    left_child_idx : int = left_child(current_idx)
    if left_child_idx >= len(elements) - 1: #注意处理左节点是最后一个元素的情况
        return (elements[left_child_idx], left_child_idx)

    right_child_idx : int = right_child(current_idx)
    if elements[left_child_idx].priority >= elements[right_child_idx].priority:
        return (elements[left_child_idx], left_child_idx)
    else:
        return (elements[right_child_idx], right_child_idx)

def  swap(elements : [Element], idx_1 : int, idx_2 : int) : #交换两个元素的内容
    if (idx_1 < 0 or idx_1 >= len(elements)) or (idx_2 < 0 or idx_2 > len(elements)):
        raise ValueError
    
    content_tmp : str = elements[idx_2].content
    priority_tmp : int = elements[idx_2].priority
    
    elements[idx_2].content = elements[idx_1].content
    elements[idx_2].priority = elements[idx_1].priority

    elements[idx_1].content = content_tmp
    elements[idx_1].priority = priority_tmp

def  push_down(elements : [Element], idx : int = 0) :
    pdb.set_trace()
    current_idx : int = idx
    while current_idx < first_leave_index(elements): #1 不是叶子节点就能往下调整
        (child , child_idx ) = highest_priority_child(elements, current_idx)
        if child.priority > elements[current_idx].priority:
            swap(elements, current_idx, child_idx)
            current_idx = child_idx
        else:
            break

我们构造一些数据来运行上面代码进行检验：

elements = [ Element('a', 1), Element('a', 8), Element('a', 5), Element('a', 7),
             Element('a', 2), Element('a', 4), Element('a', 3), Element('a', 6)
           ]
push_down(elements)

print(elements)

代码运行后所得结果如下：

[Element('a', 8), Element('a', 7), Element('a', 5), Element('a', 6), Element('a', 2), Element('a', 4), Element('a', 3), Element('a', 1)]

从输出看，结果与我们分析一致，因此确定代码实现是正确的。预知后事如何，请点击->更多精彩内容