深度学习与图神经网络核心技术实践应用高级研修班-Day3图神经网络（GNN）

Posted 2021-09-09 ZSYL

图神经网络基础和基本思想

• 1. 图神经网络
• • 1.1 图神经网络的定义和目标
  • 1.2 图神经网络的思想和工作原理
  • 1.3 图神经网络的应用场景
• 2. 图卷积神经网络
• • 2.1 图卷积神经网络的定义
  • 2.2 图卷积神经网络的卷积方式
  • 2.3 卷积神经网络与图卷积神经网络的区别
  • 2.4 图卷积神经网络的卷积方式
  • 2.5 图卷积神经网络的原理与理论推导
• 3. 图卷积神经网络的编程实例

1. 图神经网络

图神经网络（GNN）是在图域上运行的基于深度学习的方法。

由于其令人信服的性能和高解释性，GNN最近已成为一种广泛应用的图形分析方法。

1.1 图神经网络的定义和目标

定义：图神经网络（Graph Neural Network, GNN），是用于学习包含大量连接的图的联结主义模型。

目标

GNN的目标是学习到每个节点的邻居的状态嵌入，这个状态嵌入是向量且可以用来产生输出，例如节点的标记。

1.2 图神经网络的思想和工作原理

图：

图是一种数据结构，可对一组对象（节点）及其关系（边）进行建模。

图是用于机器学习的独特的非欧氏数据结构，图分析着重于节点分类，链接预测和聚类。

产生的动机

图神经网络产生的第一个动机源于卷积神经网络（CNN）

CNN具有提取多尺度局部空间特征并将其组合以构建高度表达的能力

1. 图是最典型的局部连接结构。
2. 与传统的图谱理论相比，共享权重降低了计算成本
3. 多层结构是处理分层模式的关键，它捕获了各种大小的特征。

CNN只能对诸如图像（2D网格）和文本（1D序列）之类的常规欧几里得数据进行操作。

图神经网络产生的第二个动机来自图嵌入，可以在低维向
量中表示图节点，边或子图。

图嵌入存在两个缺点：

首先，编码器中的节点之间没有共享参数，这导致计算效率低下，因为这意味着参数的数量随节点的数量线性增长。

其次，直接嵌入方法缺乏泛化能力，这意味着它们无法处理动态图或泛化为新图。

基于CNN和图嵌入，提出了图神经网络来集合图结构中的信息。 因此，图神经网络可以对包含元素及其依存关系的输入和/或输出进行建模。

此外，图神经网络可以同时使用RNN内核对图上的扩散过程进行建模。

工作原理：

图神经网络是一种直接在图结构上运行的神经网络。GNN 的一个典型应用是节点分类。本质上，图中的每个节点都与一个标签相关联，目的是预测没有 ground-truth 的节点的标签。

节点分类问题：

在节点分类问题设置中，每个节点 v 的特征 x_v 与一个 ground-truth 标签 t_v 相关联。给定一个部分标记的 graph G，目标是利用这些标记的节点来预测未标记的节点的标签。

图神经网络学习用包含邻域信息的 d 维向量 h_v 表示每个节点。即：

由于要寻找 h_v 的唯一解，可以应用 Banach 不动点定理，将上面的方程重写为一个迭代更新过程。

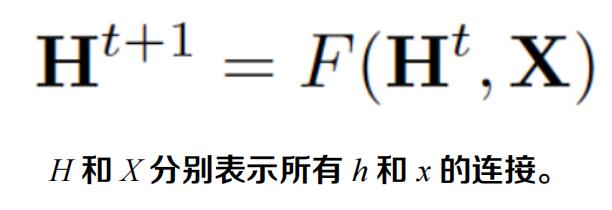
通过将状态 h_v 和特性 x_v 传递给输出函数 g，从而计算 GNN 的输出。

L1 loss 可以直接表述为：

可以通过梯度下降进行优化。

1.3 图神经网络的应用场景

2. 图卷积神经网络

2.1 图卷积神经网络的定义

图卷积网络（GCN）是一个对图数据进行操作的神经网络。

2.2 图卷积神经网络的卷积方式

2.3 卷积神经网络与图卷积神经网络的区别

空域卷积

频域卷积

频域卷积主要利用的是图傅里叶变换(Graph Fourier Transform)实现卷积。

简单来讲，它利用图的拉普拉斯矩阵(Laplacian matrix)导出其频域上的的拉普拉斯算子，再类比频域上的欧式空间中的卷积，导出图卷积的公式。

2.4 图卷积神经网络的卷积方式

空域卷积

消息传递网络(MPNN) 是由Google科学家提出的一种模型。它将空域卷积分解为两个过程：消息传递与状态更新操作，分别由M_l(⋅)和U_l(⋅)函数完成。将结点v的特征x_v作为其隐藏状态的初始态h_0_v后，空域卷积对隐藏状态的更新由如下公式表示：

其中l代表图卷积的第l层，上式的物理意义是：收到来自每个邻居的的消息M_l+1后，每个结点如何更新自己的状态。

频域卷积

傅里叶变换：

傅里叶变换(Fourier Transform, FT)会将一个在空域(或时域)上定义的函数分解成频域上的若干频率成分。换句话说，傅里叶变换可以将一个函数从空域变到频域。用 F 来表示傅里叶变换的话，有一个很重要的恒等式：

这里的F_−1指的是傅里叶逆变换，⊙是哈达玛乘积，指的是两个矩阵(或向量)的逐点乘积(Element-wise Multiplication)。

频域卷积

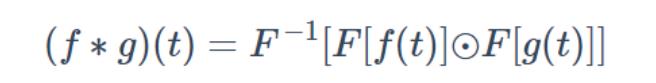
上面这个公式，它的直观含义可以用一句话来概括：空(时)域卷积等于频域乘积。简单来说就是，如果要算 f 与 g 的卷积，可以先将它们通过傅里叶变换变换到频域中，将两个函数在频域中相乘，然后再通过傅里叶逆变换转换出来，就可以得到 f 与 g 的卷积结果。

频域卷积

f经过傅里叶变换后的结果f^就如下所示，其中 i=√-1(虚数单位)， t是任意实数。

我们这里关心的实际上是 exp_−2πixt 的物理意义，它是图上类比构造傅里叶变换的关键。这个式子实际上是拉普拉斯算子Δ的广义特征函数。本质上是将函数f(t)映射到了以{exp_−2πixt}为基向量的空间中。

2.5 图卷积神经网络的原理与理论推导

频域卷积

特征向量需要满足的定义式是：对于矩阵A，其特征向量满足的条件应是矩阵与特征向量x做乘法的结果，与特征向量乘标量λ的结果一样，即满足如下等式。

拉普拉斯算子作用在$ex{p}_{-}2\pi ixt$确实满足以上特征向量的定义

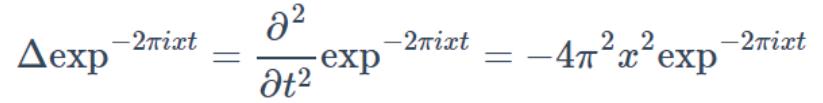
这里∂是求导符号，∂_2是二阶导。

频域卷积

在图上，如何得到拉普拉斯算子 Δ 与$ex{p}_{-}2\pi ixt$呢？

使用图的拉普拉斯矩阵(L)及其特征向量(u)，作为上述两者的替代品。

拉普拉斯矩阵，实际上是度矩阵(D)减去邻接矩阵(A) ，L=D−A，如下图所示：

频域卷积的前提条件是图必须是无向图，那么L就是对称矩阵。所以它可以按照如下公式分解:

根据上面卷积与傅里叶结合的变换公式，图上频域卷积的公式便可以写成:

如果在整个图的N个结点上一起做卷积，就可以得到整张图上的卷积如下：
重新审视一下欧式空间上的卷积和图上的卷积，即可明白图上的卷积与传统的卷积其实非常相似，这里 f 都是特征函数，g 都是卷积核：

3. 图卷积神经网络的编程实例

使用如下命令进入创建的tensorflow环境:

conda activate tensorflow

最左边有(tensorflow)字样表示进入成功:

安装所需要的库:

conda install matplotlib
conda install network
conda install --channel https://conda.anaconda.org/anaconda tensorflow-datasets

安装过程中如果遇到以下提示，请输入 y 并按回车键确认:

解压缩 gcn_tutorial-master.zip

并且将examples文件夹下的 01_karate_unsupervised.py 文件

剪切至如下目录中，如图所示:

打开windows控制台，进入tensorflow环境中，进入:

01_karate_unsupervised.py文件所在的目录中（例D:\\py\\gcn_karate）

如下图所示:

运行命令

python 01_karate_unsupervised.py

等待程序运行完成，实验结果如下图所示（实验结果可能不同）

加油!

感谢!

努力!