缺迪杰斯特拉和SPFA] 文巾解题 787. K 站中转内最便宜的航班

Posted 2021-09-09 UQI-LIUWJ

1 题目描述

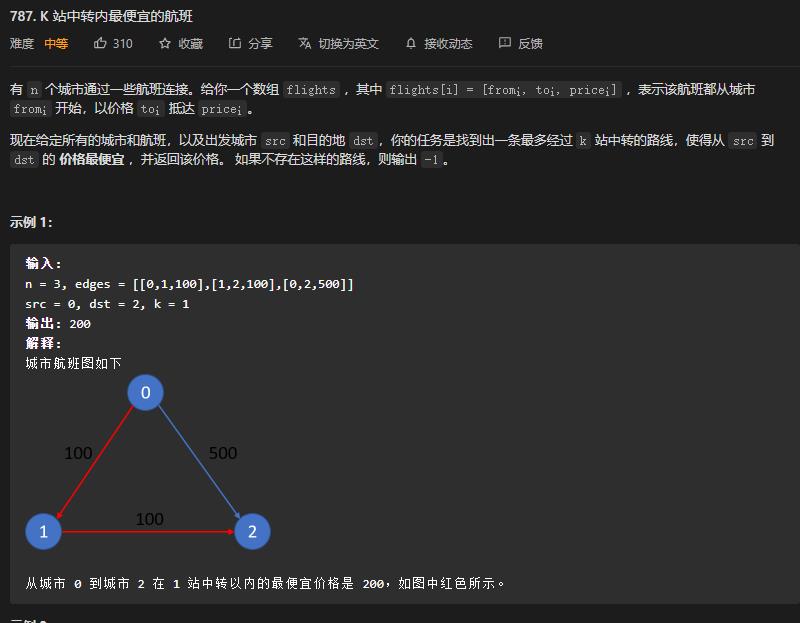
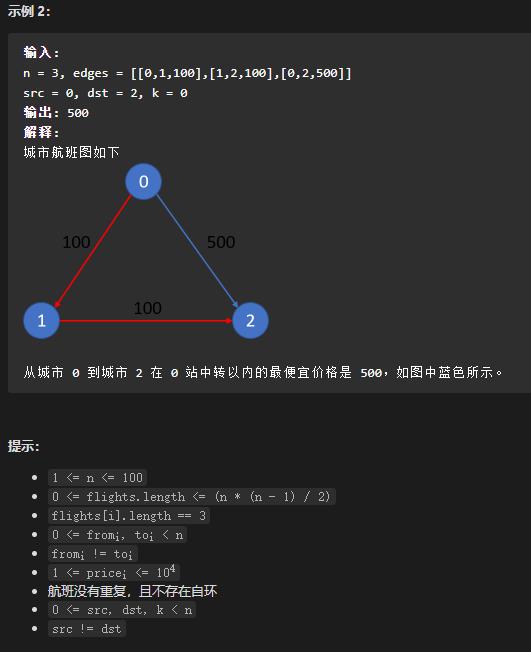
2 解题思路 

2.1 动态规划

我们记dp[i][k]表示最后一个点是k，且从src已经经过了step条边时候的距离。

那么我们最终的目标是要找到最小的dp[i][dst]（i∈[1,k+1]）

每一次的转移方程为 dp[i][dst]=min(dp[i-1][src]+len([src,dst])

于是我们使用动态规划，有：

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        INF = 10 **9
        dp = [[INF for _ in range(n)] for _ in range(k + 2)]
        dp[0][src] = 0
#所有的初始值都是无穷大，除了起始点src（因为距离src0条边距离的只有自己）

        for step in range(1, k + 2):
            for x, y, cost in flights:
                dp[step][y] = min(dp[step][y], dp[step - 1][x] + cost)
        #每一个step相当于更新 距离src更远一阶的邻居的dp信息

        res = INF
        for step in range(1, k + 2):
            res = min(res, dp[step][dst])
        #找终点中最小的dp值

        if(res==INF):
            return -1
        else:
            return res

 2.2 动态规划进阶版

我们在看一遍2.1，不难发现动态规划中的dp[i][...]只有在更新dp[i+1][....]的时候会用到，因此，我们只需要两个一维的dp数组就可以完成2.1的操作

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        INF = 10 **9
        res=INF

        dp = [INF for _ in range(n)] 
        dp[src] = 0
#相同的赋值方式

        for step in range(1, k + 2):
            dp2 = [INF for _ in range(n)] 
            for x, y, cost in flights:
                dp2[y] = min(dp2[y], dp[x] + cost)
#在这里dp2相当于当前step的dp，dp相当于上一个step的dp
            dp=dp2

            res=min(res,dp[dst])
#这一个step对应的dp[dst]值是否可以更新结果值

        if(res==INF):
            return -1
        else:
            return res
        

 

2.3 BFS 

        BFS可以做，就是需要在很多地方进行剪枝

        设立一个队列，里面的每一个元素是一个三元组：当前起始点，还剩下几条边可以走，从最初起始点到当前起始点之间的距离。

        每一次从队列中弹出一个元素(origin,num,dis)，先判断还能不能继续去下一个节点dst，如果能得话，将(dst,num-1,dis+len([origin,dst]))入队列；如果下一个节点就是终点的话，就判断是否要更新结果那个最小值

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        dit=dict()
        for i in range(n):
                dit[i]=[]
        for i in flights:
            tmp=i[0]
            dit[i[0]].append([i[1],i[2]])
#建立一个字典，字典的key是起始点，value是相邻点和起点终点之间连边的长度

        
        lst=[[src,k+1,0]]
        m=10000000

        dist=[m for _ in range(n)]
        #dist表明从最初的起点到某一个点之间的最短距离，可以用于剪枝

        while(lst):
            a=lst.pop(0)
            origin=a[0]
            num=a[1]
            dis=a[2]
            
            x=num-1
            if(x<0):
                continue
#已经没有剩余边了，剪枝

            if(dis>dist[origin]):
                continue
#从最初的原点到当前点的距离 比目前从最初的原点到当前点的最短距离长，剪枝

            dist[origin]=dis
#更新从最初的原点到当前点的距离

            for i in dit[origin]:
                    destination=i[0]
                    length=i[1]
                    long=dis+length
                    
                    if(destination==dst):
                        m=min(m,long)
#到达终点，判断要不要更新m
                    elif(long>m):
                        pass
                    else:
                        lst.append([destination,x,long])
        if(m==10000000):
            m=-1
        return(m)