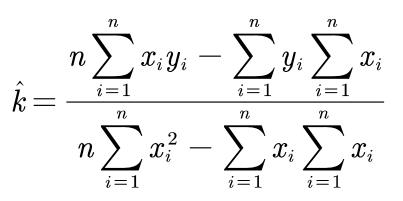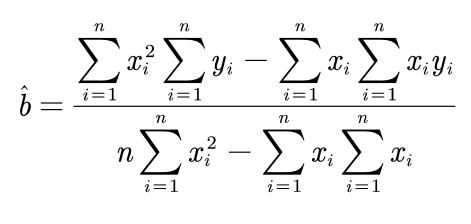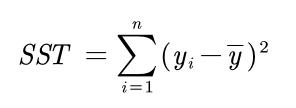MATLAB基础语法之拟合算法

Posted 2021-09-09 衾许°

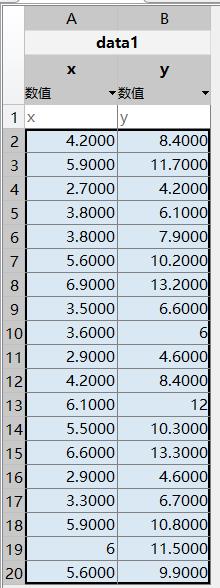
%data1.mat数据如下

---

%导入data1的数据

• load  data1

---

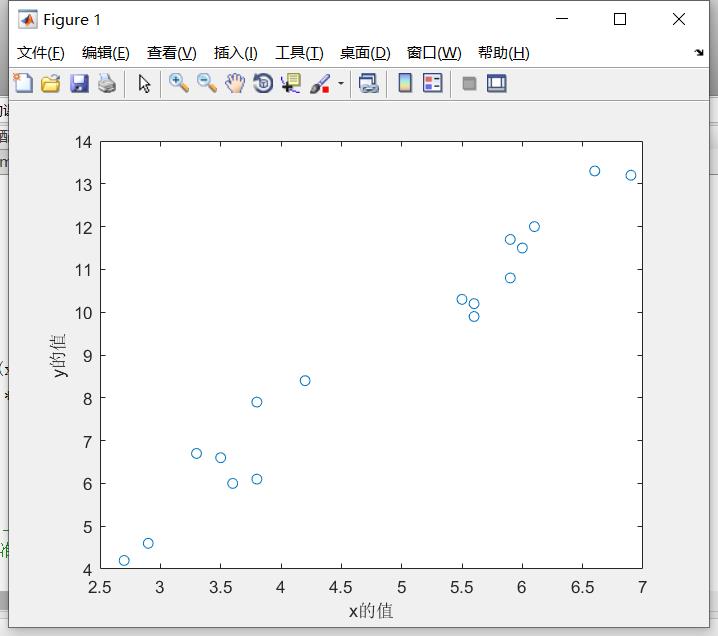
%以x为自变量，y为因变量，o为点的形状作散点图

• plot(x,y,'o')

% 给x和y轴加上标签

• xlabel('x的值')
• ylabel('y的值')

%返回data1数据行数n = 19

• n = size(x,1);               

%最小二乘法求解拟合曲线参数

• 
• k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
• 
• b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x)) 

% 继续在之前的图形上来画图形

• hold on

%显示网格线

• grid on%

% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7  % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b  % k和b都是已知值
% plot(xx,yy,'-')

% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子

•  z=@(x,y) x^2+y^2; 
•  z(1,2) % ans =  5

% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围

• f=@(x) k*x+b;
• fplot(f,[2.5,7]);
• legend('样本数据','拟合函数','location','SouthEast')

% y的拟合值

• y_hat = k*x+b;

% 回归平方和

• SSR = sum((y_hat-mean(y)).^2)  

% 误差平方和

• SSE = sum((y_hat-y).^2)

% 总体平方和

• SST = sum((y-mean(y)).^2)

% 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差

• SST-SSE-SSR  

%R^2越接近1，说明误差平方和越接近零，说明拟合效果越好。

• R_2 = SSR / SST

 补充知识：（生成随机数矩阵）

1. randi : 产生均匀分布的随机整数（i = int）  

%产生一个1至10之间的随机整数矩阵，大小为2x5；
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵，大小为1x10；
s2 = randi([-5,5],1,10)

2.rand: 产生0至1之间均匀分布的随机数

%产生一个0至1之间的随机矩阵，大小为1x5；
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵，大小为1x5；  % a + (b-a) * rand(1,5); 如：a,b = 2,5
s4= 2 + (5-2) * rand(1,5)

3.normrnd:产生正态分布的随机数

%产生一个均值为0，标准差（方差开根号）为2的正态分布的随机矩阵，大小为3x4；
s5 = normrnd(0,2,3,4)

4.roundn—任意位置四舍五入

% 0个位 1十位  2百位 -1小数点后一位  
a = 3.1415
roundn(a,-2)    % ans   =  3.1400
roundn(a,2)      % ans   =  0
a =31415
roundn(a,2)   % ans  = 31400
roundn(5.5,0)  %6
roundn(5.5,1) %10

5.人口预测例题

• year = 1790:10:2000;
• population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
• plot(year,population,'o')
• cftool  % 拟合工具箱

(1) X data 选择 year
(2) Y data 选择 population
(3) 拟合方式选择：Custom Equation (自定义方程)
(4) 修改下方的方框为：x = f(t) = xm/(1+(xm/3.9-1)*exp(-r*(t-1790)))
(5) 左边的result一栏最上面显示：Fit computation did not converge:即没有找到收敛解，右边的拟合图形也表明拟合结果不理想
(6) 点击Fit Options，修改非线性最小二乘估计法拟合的初始值(StartPoint), r修改为0.02，xm修改为500 
(7) 此时左边的result一览得到了拟合结果：r = 0.02735, xm = 342.4
(8) 依次点击拟合工具箱的菜单栏最左边的文件—Generate Code(导出代码到时候可以放在你的论文附录)，可以得到一个未命名的脚本文件
(9) 在这个打开的脚本中按快捷键Ctrl+S，将这个文件保存到当前文件夹。
(10) 在现在这个文件中调用这个函数得到参数的拟合值和预测的效果

• [fitresult, gof] = createFit(year, population)
• t = 2001:2030;
• xm = 342.4;   
• r =  0.02735;

% 计算预测值（注意这里要写成点乘和点除,这样可以保证按照对应元素进行计算）

• predictions = xm./(1+(xm./3.9-1).*exp(-r.*(t-1790)));  
• figure(2)

% 绘制预测结果图

• plot(year,population,'o',t,predictions,'.')