铺地砖（状压DP）

Posted 2021-09-09 jpphy0

目录

• 问题
• 分析
• • 扩展过程
  • 二进制与状态
  • 扩展优化
  • dp数组优化
  • 其它优化
• 代码

问题

• 求用 $1\times 2$ 的地砖铺设 $n\times m$ 的地面的方案数，地砖不能相互覆盖.
  • $1\le n\times m\le 300$
  • 结果对 $1e9+7$ 取模

分析

扩展过程

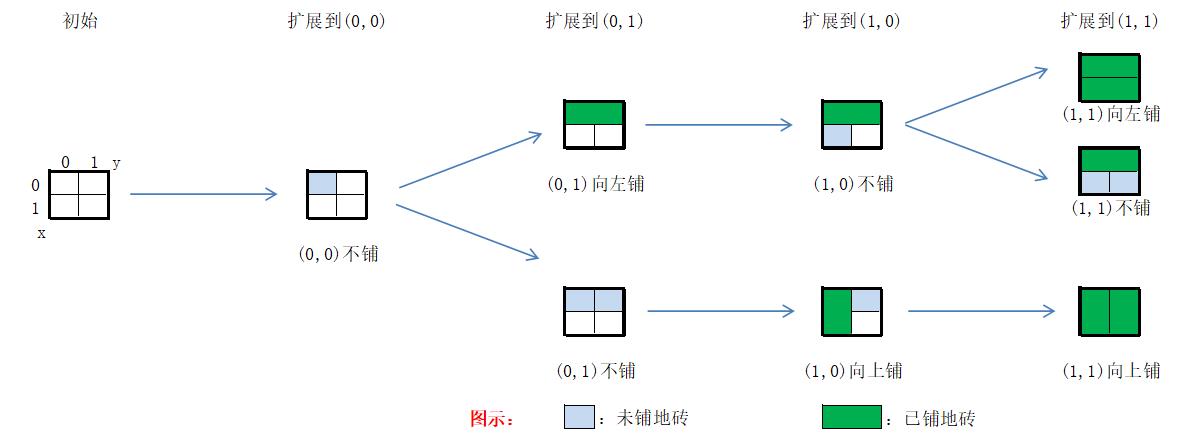
• 当某一行扩展完毕时，这一行可能铺满，也可能留有若干空缺，因此扩展结果可能有 $2^m$ 情况
• 扩展新的一行时，对于上一行的每种扩展结果都需要进行m次扩展，有可能得到 $2^m$ 结果
• 扩展过程的复杂度：$O(n\cdot 2^m\cdot 3^m)$

二进制与状态

• 一行共有m块，已铺地砖的块视为 $0$，未铺地砖的空缺块位视为 $1$，则可用m位二进制表示

扩展优化

• 使用BFS方式处理扩展过程
• 优化扩展结果表示
  • 设扩展到了 $[i][j][s]$，即第 $i$ 行第 $j$ 例，且上一行的状态是 $s$
  • 新状态的前 $j+1$位已经确定，而后 $m-j-1$ 位则尚未确定，但必定会由 $s$ 的后 $m-j-1$ 位决定
  • 显然，若新状态的前 $j+1$位 及 原状态 $s$ 的后 $m-j-1$ 位 一致时，将产生相同的结果，因此合并这些项将减少运算量
  • 合并后，状态量是m位二进制，因此每扩展一块，将得到 $2^m$ 种新状态
• 优化后，复杂度为：$O(n\cdot m\cdot 2^m)$

dp数组优化

• 维护上次扩展结果
• 维护本次扩展结果
• 显然，滚动数组即可，$pre[s]$ 和 $cur[s]$， 表示扩展结果是 $s$ 的方案的可能数量

其它优化

• 地面$n\cdot m$ 为奇数则无解
• 滚动数组的数据清除采用使用后即清除，不采用统一的 $memset$ 方式

代码

/* 铺地砖 状压dp */
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int md = 1e9+7;
const int MXS = (1<<17)+5;
ll dp[MXS<<1], *pre, *cur;
int main(){
	int t, S, N, M;
	scanf("%d", &t);	
	while(t--){
		scanf("%d%d", &N, &M);
		if(M > 17) M ^= N, N ^= M, M ^= N; // 交换
        if(N&1 && M&1) { printf("0\\n"); continue; }
		S = (1<<M)-1;
        pre = dp, cur = dp+MXS;
        memset(dp, 0, sizeof dp), pre[0] = 1; // 设定初态
		for(int n = 0; n < N; ++n){
			for(int m = 0; m < M; ++m){
				for(int s = 0; s <= S; pre[s++] = 0){
					if(pre[s] == 0) continue; // 未出现的状态
					if(s&(1<<m)){ // 向上铺
						cur[s&~(1<<m)] = (cur[s&~(1<<m)] + pre[s])%md;
						continue;
					}					
					cur[s|(1<<m)] = (cur[s|(1<<m)] + pre[s])%md; // 不铺
					if(s&(1<<m-1) && m > 0)// 向左铺
						cur[s&~(3<<m-1)] = (cur[s&~(3<<m-1)] + pre[s])%md;
				}
                swap(pre, cur);
			}
		}
        printf("%d\\n", pre[0]);
	}
    return 0;
}