CCF201709-4 通信网络（100分）DFS+BFS

Posted 2021-09-09 海岛Blog

试题编号： 201709-4
试题名称： 通信网络
时间限制： 1.0s
内存限制： 256.0MB
问题描述：

问题描述
　　某国的军队由N个部门组成，为了提高安全性，部门之间建立了M条通路，每条通路只能单向传递信息，即一条从部门a到部门b的通路只能由a向b传递信息。信息可以通过中转的方式进行传递，即如果a能将信息传递到b，b又能将信息传递到c，则a能将信息传递到c。一条信息可能通过多次中转最终到达目的地。
　　由于保密工作做得很好，并不是所有部门之间都互相知道彼此的存在。只有当两个部门之间可以直接或间接传递信息时，他们才彼此知道对方的存在。部门之间不会把自己知道哪些部门告诉其他部门。

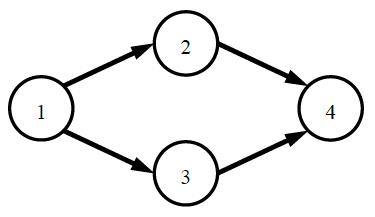
上图中给了一个4个部门的例子，图中的单向边表示通路。部门1可以将消息发送给所有部门，部门4可以接收所有部门的消息，所以部门1和部门4知道所有其他部门的存在。部门2和部门3之间没有任何方式可以发送消息，所以部门2和部门3互相不知道彼此的存在。
　　现在请问，有多少个部门知道所有N个部门的存在。或者说，有多少个部门所知道的部门数量（包括自己）正好是N。
输入格式
　　输入的第一行包含两个整数N, M，分别表示部门的数量和单向通路的数量。所有部门从1到N标号。
　　接下来M行，每行两个整数a, b，表示部门a到部门b有一条单向通路。
输出格式
　　输出一行，包含一个整数，表示答案。
样例输入
4 4
1 2
1 3
2 4
3 4
样例输出
2
样例说明
　　部门1和部门4知道所有其他部门的存在。
评测用例规模与约定
　　对于30%的评测用例，1 ≤ N ≤ 10，1 ≤ M ≤ 20；
　　对于60%的评测用例，1 ≤ N ≤ 100，1 ≤ M ≤ 1000；
　　对于100%的评测用例，1 ≤ N ≤ 1000，1 ≤ M ≤ 10000。

问题链接：CCF201709-4 通信网络
问题简述：（略）
问题分析：图连通性问题，可以用DFS来解决，也可以用BFS来解决。用DFS来解决时，要使得DFS函数通用化，程序代码可以更加简洁，不过需要付出参数传递的时间代价。
程序说明：（略）
参考链接：（略）
题记：（略）

100分的C++语言程序（DFS）如下：

/* CCF201709-4 通信网络 */

#include <bits/stdc++.h>

using namespace std;

const int N = 1000 + 1;
vector<int> g1[N], g2[N];
bool vis1[N], vis2[N];

void dfs(int u, vector<int> g[], bool vis[])
{
    vis[u] = true;
    for (int v = 0; v < (int)g[u].size(); v++)
        if (!vis[g[u][v]]) dfs(g[u][v], g, vis);
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(NULL);
    cout.tie(NULL);

    int n, m, u, v;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> u >> v;
        g1[u].push_back(v);
        g2[v].push_back(u);
    }

    int ans = 0;
    for (int i = 1; i <= n; i++) {
        memset(vis1, false, sizeof vis1);
        dfs(i, g1, vis1);

        memset(vis2, false, sizeof vis2);
        dfs(i, g2, vis2);

        int flag = 1;
        for (int j = 1; j <= n; j++)
            if (!vis1[j] && !vis2[j]) {
                flag = 0;
                break;
            }
        if (flag) ans++;
    }

    cout << ans << endl;

    return 0;
}

100分的C++语言程序（BFS）如下：

/* CCF201709-4 通信网络 */

#include <bits/stdc++.h>

using namespace std;

const int N = 1000 + 1;
vector<int> g[N], g2[N];
bool vis[N], vis2[N];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(NULL);
    cout.tie(NULL);

    int n, m, u, v;
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        cin >> u >> v;
        g[u].push_back(v);
        g2[v].push_back(u);
    }

    int ans = 0;
    for (int i = 1; i <= n; i++) {
        queue<int> q;

        memset(vis, false, sizeof vis);
        q.push(i);
        vis[i] = true;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            for  (int  j = 0; j < (int)g[u].size(); j++)
                if (!vis[g[u][j]]) {
                    vis[g[u][j]] = true;
                    q.push(g[u][j]);
                }
        }

        memset(vis2, false, sizeof vis2);
        q.push(i);
        vis2[i] = true;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            for  (int  j = 0; j < (int)g2[u].size(); j++)
                if (!vis2[g2[u][j]]) {
                    vis2[g2[u][j]] = true;
                    q.push(g2[u][j]);
                }
        }

        int cnt = 0;
        for (int i = 1; i <= n; i++)
            if (vis[i] || vis2[i]) cnt++;
        if (cnt == n) ans++;
    }

    cout << ans << endl;

    return 0;
}