深度学习和目标检测系列教程 19-300：关于目标检测APIoU和mAP简介

Posted 2021-09-09 刘润森！

@Author：Runsen

R-CNN 和YOLO等对象检测模型，使用了平均精度 (mAP)。mAP 将真实边界框与检测到的框进行比较并返回分数。分数越高，模型的检测就越准确。

Precision and Recall

现在有两个类，Positive和Negative，这里是 10 个样本的真实标签。

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive"]

当这些样本被送到模型时，它会返回以下预测分数。基于这些分数，我们如何对样本进行分类（即为每个样本分配一个类标签）？

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3]

为了将分数转换为类标签，使用了阈值。当分数等于或高于阈值时，将样本归为一类。否则，它被归类为其他类。如果样本的分数高于或等于阈值，则该样本为正样本。否则，它是Negative。下一段代码将分数转换为阈值为0.5 的类标签。

import numpy

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3]
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive"]

threshold = 0.5
y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]
print(y_pred)

输出如下

['positive', 'negative', 'positive', 'positive', 'positive', 'positive', 'negative', 'negative', 'negative', 'negative']

基于y_true和y_pred，可以计算混淆矩阵、精度和召回率。

r = numpy.flip(sklearn.metrics.confusion_matrix(y_true, y_pred))
print(r)

precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(precision)

recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
print(recall)

输出如下

# Confusion Matrix
[[4 2]
 [1 3]]

# Precision = 4/(4+1)
0.8

# Recall = 4/(4+2)
0.6666666666666666

给出的精度和召回率的定义，精度越高，模型在将样本分类为Positive时就越有信心。召回率越高，模型正确分类为Positive 的正样本越多。

精确率-召回率曲线

当模型召回率高但精度低时，该模型正确分类了大部分正样本，但有很多误报（即，将许多Negative样本分类为Positive）。当模型精度高但召回率低时，该模型将样本分类为Positive时是准确的，但它可能仅对部分正样本进行分类。

对此，有一个概念精确率-召回率曲线，显示了不同阈值下精确率和召回率值之间的权衡。该曲线有助于选择最佳阈值和最大化这两个指标。

创建精确召回曲线需要一些输入：

• 真实标签。
• 样本的预测分数。
• 将预测分数转换为类标签的一些阈值。

import numpy

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive", "negative", "positive", "positive", "positive", "positive", "negative", "negative", "negative"]

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.4, 0.2, 0.4, 0.3, 0.7, 0.5, 0.8, 0.2, 0.3, 0.35]

thresholds = numpy.arange(start=0.2, stop=0.7, step=0.05)

以下是thresholds列表中保存的阈值。因为有 10 个阈值，所以将创建 10 个精度和召回值。

[0.2, 
 0.25, 
 0.3, 
 0.35, 
 0.4, 
 0.45, 
 0.5, 
 0.55, 
 0.6, 
 0.65]

precision_recall_curve函数接受真实标签、预测分数和阈值。它返回两个表示精度和召回值的等长列表。

import sklearn.metrics

def precision_recall_curve(y_true, pred_scores, thresholds):
    precisions = []
    recalls = []
    
    for threshold in thresholds:
        y_pred = ["positive" if score >= threshold else "negative" for score in pred_scores]

        precision = sklearn.metrics.precision_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        recall = sklearn.metrics.recall_score(y_true=y_true, y_pred=y_pred, pos_label="positive")
        
        precisions.append(precision)
        recalls.append(recall)

    return precisions, recalls

precisions, recalls = precision_recall_curve(y_true=y_true, 
                                             pred_scores=pred_scores,
                                             thresholds=thresholds)

以下是precisions列表中的返回值。

[0.5625,
 0.5714285714285714,
 0.5714285714285714,
 0.6363636363636364,
 0.7,
 0.875,
 0.875,
 1.0,
 1.0,
 1.0]

这是列表中的值recalls列表。

[1.0,
 0.8888888888888888,
 0.8888888888888888,
 0.7777777777777778,
 0.7777777777777778,
 0.7777777777777778,
 0.7777777777777778,
 0.6666666666666666,
 0.5555555555555556,
 0.4444444444444444]

给定长度相等的两个列表，可以在二维图中绘制它们的值，如下所示。

from matplotlib import pyplot as plt
plt.plot(recalls, precisions, linewidth=4, color="red")
plt.xlabel("Recall", fontsize=12, fontweight='bold')
plt.ylabel("Precision", fontsize=12, fontweight='bold')
plt.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
plt.show()

精确召回曲线如下图所示。

请注意，随着召回率的增加，精度会降低。

原因是当正样本数量增加时（高召回率），每个样本正确分类的准确率下降（低准确率）。这是意料之中的，因为当有很多样本时，模型更有可能失败。

精确率-召回率曲线可以很容易地确定精确率和召回率都高的点。根据上图，最好的一点是(recall, precision)=(0.778, 0.875)。

f1指标

由于曲线并不复杂，因此可以使用上图以图形方式确定精度和召回率的最佳值。更好的方法是使用称为f1分数的指标，该指标根据下一个等式计算。

该f1指标衡量准确率和召回率之间的平衡。当的值f1高时，这意味着精度和召回率都很高。较低的f1分数意味着准确率和召回率之间的不平衡更大。

根据前面的例子，f1根据下面的代码计算。根据f1列表中的值，最高分是0.82352941。它是列表中的第 6 个元素（即索引 5）。recalls和precisions列表中的第 6 个元素分别是0.778和0.875。对应的阈值为0.45。

f1 = 2 * ((numpy.array(precisions) * numpy.array(recalls)) / (numpy.array(precisions) + numpy.array(recalls)))

输出如下

[0.72, 
 0.69565217, 
 0.69565217, 
 0.7,
 0.73684211,
 0.82352941, 
 0.82352941, 
 0.8, 
 0.71428571, 0
 .61538462]

下图以蓝色显示了对应于召回率和精度之间最佳平衡点的位置。平衡精度和召回率的最佳阈值是0.45精度为0.875和召回率为0.778。

plt.plot(recalls, precisions, linewidth=4, color="red", zorder=0)
plt.scatter(recalls[5], precisions[5], zorder=1, linewidth=6)
plt.xlabel("Recall", fontsize=12, fontweight='bold')
plt.ylabel("Precision", fontsize=12, fontweight='bold')
plt.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
plt.show()

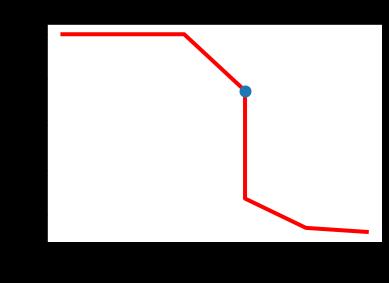
平均精度 (AP)

平均精确度（AP）是总结了精确召回曲线成表示平均精度所有的单个值的一种计算方法。

AP = np.sum((np.array(recalls[:-1]) - np.array(recalls[1:])) * precisions[:-1])
AP

输出如下

0.44543650793650796

下面总结了计算 AP 的步骤：

• 使用模型生成预测分数。
• 将预测分数转换为类标签。
• 计算混淆矩阵。
• 计算准确率和召回率指标。
• 创建精确召回曲线。
• 测量平均精度。

IoU

IoU 是是将 2 个框之间的交集面积除以它们的联合面积。IoU 越高，预测越好。

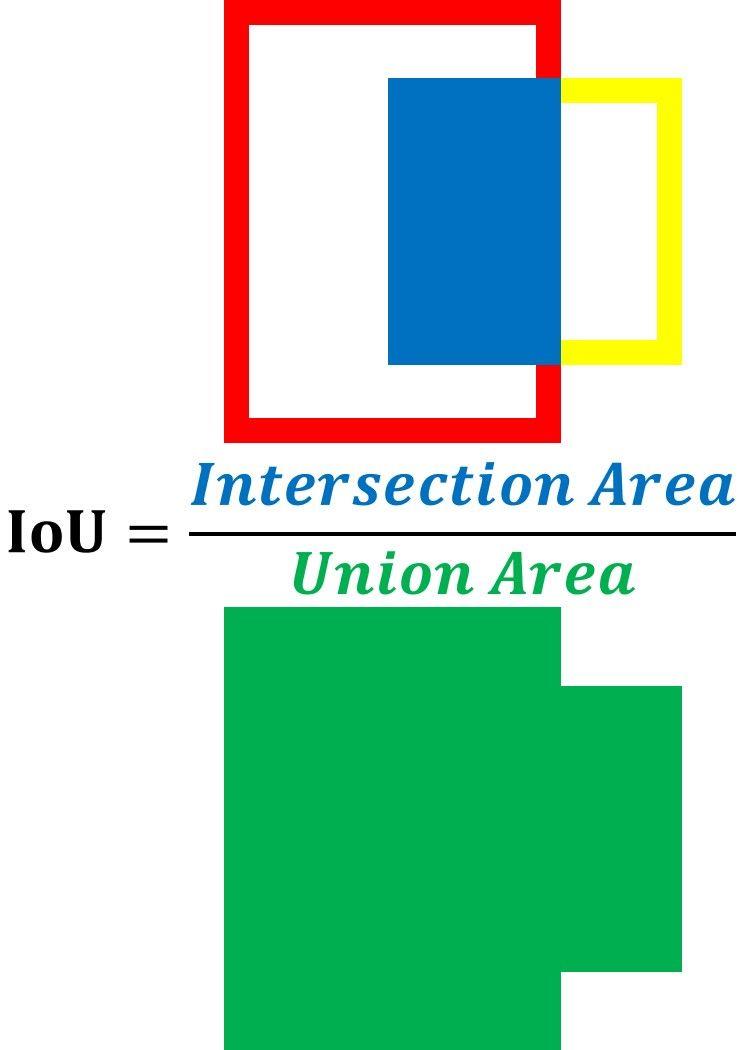
计算图像的 IoU，这里有一个名为 的函数intersection_over_union()。它接受以下 2 个参数：

def intersection_over_union(gt_box, pred_box):
    inter_box_top_left = [max(gt_box[0], pred_box[0]), max(gt_box[1], pred_box[1])]
    inter_box_bottom_right = [min(gt_box[0]+gt_box[2], pred_box[0]+pred_box[2]), min(gt_box[1]+gt_box[3], pred_box[1]+pred_box[3])]

    inter_box_w = inter_box_bottom_right[0] - inter_box_top_left[0]
    inter_box_h = inter_box_bottom_right[1] - inter_box_top_left[1]

    intersection = inter_box_w * inter_box_h
    union = gt_box[2] * gt_box[3] + pred_box[2] * pred_box[3] - intersection
    
    iou = intersection / union

    return iou, intersection, union

传递给函数的边界框是一个包含 4 个元素的列表，它们是：

左上角的 x 轴，左上角的 y 轴，宽度和高度。

gt_box = [320, 220, 680, 900]
pred_box = [500, 320, 550, 700]

鉴于图像名为cat.jpg，这是在图像上绘制边界框的完整内容。

import cv2
import matplotlib.pyplot
import matplotlib.patches

def intersection_over_union(gt_box, pred_box):
    inter_box_top_left = [max(gt_box[0], pred_box[0]), max(gt_box[1], pred_box[1])]
    inter_box_bottom_right = [min(gt_box[0]+gt_box[2], pred_box[0]+pred_box[2]), min(gt_box[1]+gt_box[3], pred_box[1]+pred_box[3])]

    inter_box_w = inter_box_bottom_right[0] - inter_box_top_left[0]
    inter_box_h = inter_box_bottom_right[1] - inter_box_top_left[1]

    intersection = inter_box_w * inter_box_h
    union = gt_box[2] * gt_box[3] + pred_box[2] * pred_box[3] - intersection
    
    iou = intersection / union

    return iou, intersection, union

im = cv2.imread("cat.jpg")

gt_box = [320, 220, 680, 900]
pred_box = [500, 320, 550, 700]

fig, ax = matplotlib.pyplot.subplots(1)
ax.imshow(im)

gt_rect = matplotlib.patches.Rectangle((gt_box[0], gt_box[1]),
                                       gt_box[2],
                                       gt_box[3],
                                       linewidth=5,
                                       edgecolor='r',
                                       facecolor='none')

pred_rect = matplotlib.patches.Rectangle((pred_box[0], pred_box[1]),
                                         pred_box[2],
                                         pred_box[3],
                                         linewidth=5,
                                         edgecolor=(1, 1, 0),
                                         facecolor='none')
ax.add_patch(gt_rect)
ax.add_patch(pred_rect)

ax.axes.get_xaxis().set_ticks([])
ax.axes.get_yaxis().set_ticks([])

iou, intersect, union = intersection_over_union(gt_box, pred_box)
print(iou, intersect, union)

0.5409582689335394 350000 647000

IoU 分数0.54意味着真实边界框和预测边界框之间有 54% 的重叠。

对象检测的平均精度 (mAP)

通常，对象检测模型使用不同的 IoU 阈值进行评估，其中每个阈值可能会给出与其他阈值不同的预测。假设模型由一个图像提供，该图像具有分布在 2 个类中的 10 个对象。如何计算mAP？

要计算 mAP，首先要计算每个类的 AP。所有类别的 AP 的平均值是 mAP。

假设使用的数据集只有 2 个类。对于第一类，这里分别是y_true和pred_scores变量中的真实标签和预测分数

y_true = ["positive", "negative", "positive", "negative", "positive", "positive", "positive", "negative", "positive", "negative"]

pred_scores = [0.7, 0.3, 0.5, 0.6, 0.55, 0.9, 0.75, 0.2, 0.8, 0.3]

这是第二个类的y_true和pred_scores变量。

y_true = ["negative", "positive", "positive", "negative", "negative", "positive", "positive", "positive", "negative", "positive"]

pred_scores = [0.32, 0.9, 0.5, 0.1, 0.25, 0.9, 0.55, 0.3, 0.35, 0.85]

IoU 阈值列表从 0.2 到 0.9，步长为 0.25。

thresholds = numpy.arange(start=0.2, stop=0.9, step=0.05)

要计算一个类的 AP，只需将其y_true和pred_scores变量提供给下一个代码。

precisions, recalls = precision_recall_curve(y_true=y_true, 
                                             pred_scores=pred_scores, 
                                             thresholds=thresholds)

matplotlib.pyplot.plot(recalls, precisions, linewidth=4, color="red", zorder=0)

plt.xlabel("Recall", fontsize=12, fontweight='bold')
plt.ylabel("Precision", fontsize=12, fontweight='bold')
plt.title("Precision-Recall Curve", fontsize=15, fontweight="bold")
plt.show()

precisions.append(1)
recalls.append(0)

precisions = numpy.array(precisions)
recalls = numpy.array(recalls)

AP = np.sum((np.array(recalls[:-1]) - np.array(recalls[1:])) * precisions[:-1])
print(AP)

对于第一类，这是它的精确召回曲线。根据该曲线，AP 为0.949。

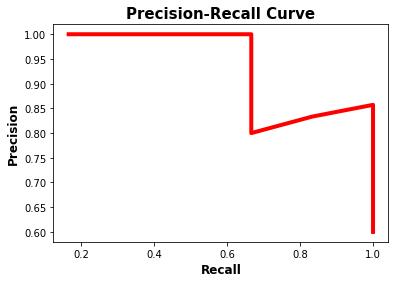
第二类的precision-recall曲线如下所示。它的 AP 是0.958.

基于 2 个类（0.949 和 0.958）的 AP，根据下一个方程计算对象检测模型的 mAP。

因此mAP 为0.9535。