立体视觉入门指南：对级约束与Fusiello法极线校正

Posted 2021-09-08 李迎松~

亲爱的同学们，我们的世界是3D世界，我们的双眼能够观测三维信息，帮助我们感知距离，导航避障，从而翱翔于天地之间。而当今世界是智能化的世界，我们的科学家们探索各种机器智能技术，让机器能够拥有人类的三维感知能力，并希望在速度和精度上超越人类，比如自动驾驶导航中的定位导航，无人机的自动避障，测量仪中的三维扫描等，都是高智机器智能技术在3D视觉上的具体实现。

立体视觉是三维重建领域的重要方向，它模拟人眼结构用双相机模拟双目，以透视投影、三角测量为基础，通过逻辑复杂的同名点搜索算法，恢复场景中的三维信息。它的应用十分之广泛，自动驾驶、导航避障、文物重建、人脸识别等诸多高科技应用都有它关键的身影。

本课程将带大家由浅入深的了解立体视觉的理论与实践知识。我们会从坐标系讲到相机标定，从被动式立体讲到主动式立体，甚至可能从深度恢复讲到网格构建与处理，感兴趣的同学们，来和我一起探索立体视觉的魅力吧！

本课程是电子资源，所以行文并不会有太多条条框框的约束，但会以逻辑清晰、浅显易懂为目标，水平有限，若有不足之处，还请不吝赐教！
个人微信：EthanYs6，加我申请进技术交流群 StereoV3D，一起技术畅聊。
CSDN搜索 ：Ethan Li 李迎松，查看网页版课程。
随课代码，将上传至github上，地址：StereoV3DCode：https://github.com/ethan-li-coding/StereoV3DCode

让大家久等了，最近工作变动，尚在适应中，望大家海量！

在前面的博文中，我们已经介绍完了基础知识和相机标定，同学们一定想着下一步该往那个方向，在相机标定之后，相机的位姿就确定了，而接下来，拿着相机采集图像是自然会发生的事情，那采集完图像之后呢？我们该做什么呢？

回到立体视觉的最终目标，是通过对图像做双视匹配计算场景的三维坐标，在这入门系列，我不得不得提前解释下什么叫双视匹配，特别是匹配二字的含义。

匹配，英文是match，从字面意义来说，是将N（N>=2）个目标配到一起，这N个目标通常有一些共同或者近似的属性，比如一对耳机的左右两只，他们是同属于一副耳机，比如你和你的兄弟姐们，你们都是你爸妈的孩子。自然地，双视匹配，就是在两个视图中，寻找共同属性的像素点配成对，在立体视觉里，这个共同属性是：它们是空间中同一个点在各自视图的投影，也就是说它们代表了空间中的同一个点。

那为何要做双视匹配呢？这要从三角测量说起，

三角测量是非常简单的一个概念，指的是确定两个点和从两个点出发的射线，就可以计算出两条射线相交的另一个点坐标，三个点形成一个三角关系，所以叫三角测量。

对应到立体视觉里面，三个点分别是：两个相机的光心点和一个空间点，光心的位置通过标定确定，而两条射线是两光心各自和空间点的连线，如果再确定了两条射线，就可以计算出空间点的坐标，有人问，怎么确定两条射线呢？那就是匹配要干的事情了。

我们在上图中加点东西，左边两个点为两个相机的光心$C$，右边的一个点为空间点$P$，在光心前面加上像平面$I$（我在前面博文中就已经说过，像平面的其实是在光心的后方，拿到前面来是等价的，但是理解起来更直观一些）。空间点和光心的连线与像平面的交点为$p$。

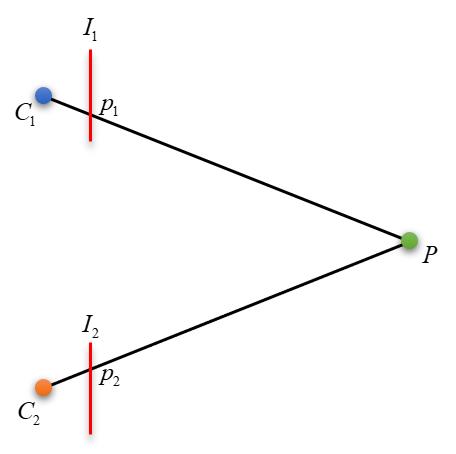
从另一个角度来说，$p$是空间点$P$在图像上的投影点，也就是我们在图像上看到物体的的成像。

好了，回到前面的问题，怎么确定射线$C_{1}P,C_{2}P$呢？显然，图中有一个很明显的恒等关系是，$C_{1}P\equiv C_1{p}_1,C_{2}P\equiv C_2{p}_2$，所以确定射线$C_{1}P,C_{2}P$可以转换成确定射线$C_1{p}_1,C_2{p}_1$。$C_1,C_2$我们已经通过标定得到了，而$p_1,p_2$的确定过程就称为匹配了。一般情况下，我们给定一个像素$p_1$，在另外一个视图中寻找对应的匹配点$p_2$，找到了就可以计算$P$了。

好了，关于匹配的定义就说到这里。我们回到今天的主题：对极约束。

为什么研究对极约束

在计算机科学中，给定一个确定的问题，一定会有各种算法从研究如何解决它，再上升到如何高效的解决它，而它们也不是依次进行，而是交叉地，即研究最确定解和研究最高效解是同步进行的。而对于匹配问题而言，寻找对应匹配点对这个问题，实在不是个简单问题，几十年来，没有一个算法能完美寻找所有正确匹配点对，角度产生的图像之间的仿射扭曲、弱纹理、重复纹理、暗光、过曝、透明等等，头疼的问题确实非常多，而且有些看上去是无解的，但这丝毫不妨碍众多学者们研究对该问题的浓厚兴趣，从而产生了很多优秀的算法，有很多在实际工程应用中被证明是精确且高效的（这里的精确并不是说它们是几何意义上的精确，而是说工程意义上的精确）。

回到正题，熟悉一点优化思想的人都知道，一旦涉及到搜索空间这个词，就会有人自然而然的想到如何减少搜索空间来提高搜索效率，毕竟我们的计算机是三维空间的人设计的，它的运动也准循着三维空间的规律，没有高维空间折叠能力，在搜索这件事上还是要受限制于空间的大小和距离，但是我们可以也做几件事情：

1. 让它的运动空间变小。
2. 让它在不存在目标点的位置少做停留。

我们的对级约束就是为了做第一件事，让匹配的搜索空间变小，略去完全不可能是解的像素。简单来说，作为匹配对的两个像素，一定会满足一个约束公式，如果不满足则肯定不是匹配点。这样可以省去非常多的无意义搜索，但稍显遗憾的是，这个约束不是唯一约束，也就是说对于左视图上一个像素点，在右视图上还是会有很多像素满足这个约束，所以只能缩小搜索空间，不能直接确定解。

对极约束，是将搜索空间约束到像平面内的一条直线上，这个我们下面慢慢来说。

极平面和极线

对极约束是怎么来的呢？我们看下图：

图1 对级约束

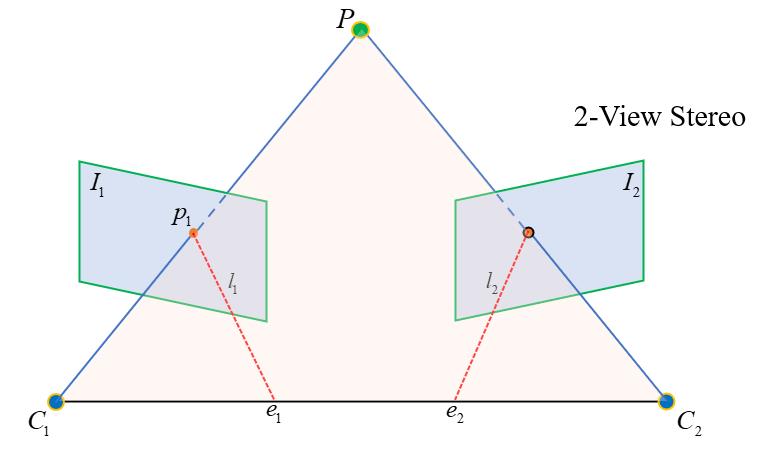
光心$O_1,O_2$（原谅我换了个符号）和空间点$P$形成一个三角关系，实际上它们确定了一个空间平面，这个平面和两个像平面都相交，交线分别是$l_1,l_2$，发挥我们的想象力，很容易发现，在$l_1$上的所有点，他的匹配点一定在$l_2$上，这就是对极约束，它将匹配的搜索空间限制到了一条直线上，大大减少了搜索的空间大小，提高匹配效率。而两条直线$l_1,l_2$就叫做极线，我们可以称它们两为极线对。这个概念大家记一下，后面会出现。

那怎么确定这条直线呢？我们已知$O_1,O_2,p$，可以计算平面$O_{1}p{O}_2$的方程，它和像平面$I_2$（就是$p_2$所在的像平面）相交的直线即为$l_2$，有了$l_2$的方程就可以在像平面$I_2$里挨个遍历位于线$l_2$上的像素了。在稀疏点匹配里，我们就可以这样做从而提高搜索效率。

极线校正

好了，上面我们讲了对级约束，大家明白了它的概念和空间意义，下面我还要讲一个重要的概念：极线校正，同样要问一句，为什么要讲它，在上面一章中我们提到，对级约束可以让我们减小搜索空间，有了对级约束，对于左视图的一个像素点$p_1$，可以计算出右视图中匹配点$p_2$所在的那条极线$l_2$，从而在$l_2$上搜索正确解。听上去确实不错，大大减少了搜索空间，但它还是存在一个缺点，就是对于左视图的每个待匹配像素，都要计算它对应的那条极线，如果我的待匹配像素非常多（这正是稠密匹配的研究方向：逐像素匹配），那计算量还是挺大的。

有没有一种方法，可以不用计算，直接确定右边的极线呢？

答案当然是有，极线校正就是来回答这个问题！

还是观察上图，我们会进一步发现，极线$l_1$上的所有像素和$l_2$上的像素满足同一种约束公式呢，也就是说极线$l_1$上的所有像素，算出的对应极线，都是同一条$l_2$。究其原因，是因为它们都属于同一个极平面呀！所以可以这样认为，一个极平面就可以在两个视图上找到一对极线，这对极线上的所有像素满足同一个约束公式，而多个极平面就产生了多个极线对，众多的极线对可以涵盖图像上的所有像素点！

进一步，我们可以将这些极线对上的像素重排列在像平面，同一对极线上的像素排列到同一行，这样我们就可以通过行号来确定同一极线对的像素，不用在计算极线方程了。简言之，左视图像素$p_1$的匹配点一定位于右视图行号相同的那一行像素内。

以上是对于极线校正的一个简单的意义解释。而从几何上来说，我们有更专业的解释：

极线校正是通过对两个相机进行旋转，并重新定义新的像平面，让极线对共线且平行于像平面的某条坐标轴（通常是水平轴），该操作同时建立了新的立体像对。纠正完成后，同一匹配点对，位于两个视图的同一行内，这意味着它们只有水平坐标（或者说列坐标）的差异，这个差异称为视差（简写$d$），数学定义上，视差$d=col(p_1)-col(p_2)$（$col$指水平方向坐标，或者说列坐标$）

图2 极线校正 *图片来源：Mattoccia S , Updates S M , Outline S M . Stereo Vision: Algorithms and Applications[J]. 2011.*

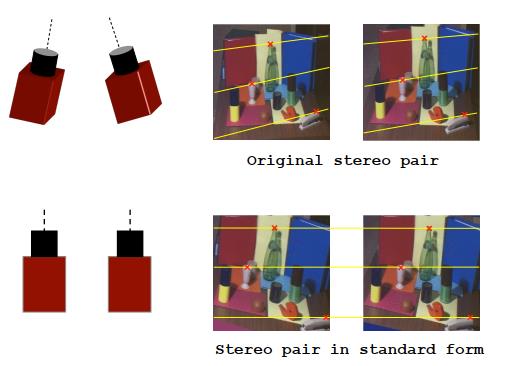
这个操作使得稠密匹配变得容易很多，当然，只是相对容易了。

解释完极线校正的概念和意义，我们关心的另一件事是，如何做极线校正？

这就有不同的方式来完成，今天我们主要来讲一讲Fusiello校正法。

我们先来看看我们的目标：

1. 极线对平行于某条坐标轴。
2. 极线对共线，匹配点对位于像平面的同一行。

为达到这两个目标，我们要进行不同分析，前面说到，极线校正是通过旋转相机和重新定义像平面来做，实际上，两个操作的本质在于重新定义投影矩阵$M=K[R|-RC]$。通过旋转相机重定义旋转矩阵 R →

以上是关于立体视觉入门指南：对级约束与Fusiello法极线校正的主要内容，如果未能解决你的问题，请参考以下文章

立体视觉入门指南：对级约束与Fusiello法极线校正

立体视觉入门指南：对级约束与Fusiello法极线校正

立体视觉入门指南：对级约束与Fusiello法极线校正

（一) 双目立体视觉介绍

双目立体匹配中的核线约束[极线约束]

SLAM入门之视觉里程计：基础矩阵的估计