堆排序(HeapSort)

Posted 2021-09-08 清水寺扫地僧

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了堆排序(HeapSort)相关的知识，希望对你有一定的参考价值。

文章目录

1. 堆的概念

堆的数据结构也即是个顺序存储的完全二叉树。在STL容器当中的实现为 $priority\\_queue$ ，即优先队列。
之前左神的视频中已经讲过，昨日腾讯音乐一面要求写堆排序，时间比较久远且当时的代码也比较复杂。因此，在这里重新整理一下。之前的实现方法见：排序归纳总结（插入排序、归并排序、堆排序、快速排序、桶排序）——3. 堆排序。

其中每个结点的关键字都不大于其孩子结点的关键字，这样的堆称为小根堆。
其中每个结点的关键字都不小于其孩子结点的关键字，这样的堆称为大根堆。

2. 堆的实例

举例来说，对于 $n$ 个元素的序列 ${nums_0, nums_1, ... , nums_n}$ 当且仅当满足下列关系之一时，称之为堆：
(1) $nums_i <= num_{2i+1}$ 且 $nums_i <= num_{2i+2}$ (小根堆)
(2) $nums_i >= num_{2i+1}$ 且 $nums_i >= num_{2i+2}$ (大根堆)
其中 $i=1,2,…,\\frac{n}{2}$ 向下取整;

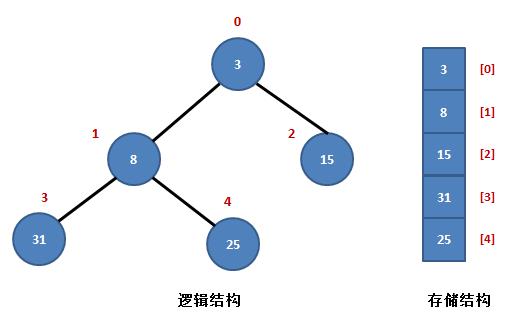
如上图所示，序列 $nums\\{3, 8, 15, 31, 25\\}$ 是一个典型的小根堆。
堆中有两个父结点（ $floor(\\frac{5}{2}) = 2$ ，这里父节点的个数可以理解为子树的个数），元素 $3$ 和元素 $8$ 。
元素 $3$ 在数组中以 $n u m s [0]$ 表示，它的左孩子结点是 $n u m s [1]$ ，右孩子结点是 $n u m s [2]$ 。
元素 $8$ 在数组中以 $n u m s [1]$ 表示，它的左孩子结点是 $n u m s [3]$ ，右孩子结点是 $n u m s [4]$ ，它的父结点是 $n u m s [0]$ 。

可以看出，它们满足以下规律：
设当前元素在数组中以 $n u m s [i]$ 表示，那么:

(1) 它的左孩子结点是： $n u m s [2 i + 1]$ ;
(2) 它的右孩子结点是： $n u m s [2 i + 2]$ ;
(3) 它的父结点是： $nums[\\frac{i-1}{2}]$ ;
(4) $n u m s [i] < = n u m s [2 i + 1]$ 且 $n u m s [i] < = n u m s [2 i + 2]$ （小根堆特征）。

3. 堆排过程

3.1 堆排思想

堆排序基本思想：将待排序序列（元素数目为 $n$ ）构造为一个大/小顶堆，此时，整个序列的最大/小值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大/小值。然后将剩余 $n - 1$ 个元素重新构造成一个堆，这样会得到 $n$ 个元素的次小值。如此反复执行，便可得到一有序序列了。

具体操作层面上为：

(1) 根据初始数组去构造初始堆（构建一个完全二叉树，保证所有的父结点都比它的孩子结点数值大/小，构建过程只需从非叶子节点进行逆序调整即可，次第对父节点沿着深搜路径(从根节点到叶子节点)进行顺序调整）；
(2) 每次交换第一个和最后一个元素，输出最后一个元素（最大/小值），然后把剩下元素重新调整为大/小根堆；

3.2 堆排过程示意

以无序序列 ${ 1, 3, 4, 5, 2, 6, 9, 7, 8, 0 \\}$ 的升序排序为例：

(1) 构建初始大根堆：

(2) 取出最大值放置到序列末尾，除开序列末尾将剩余元素重新调整为大根堆，重复该操作直至剩余元素的个数为1：

3.3 堆排代码实现

代码实现，使用LeetCode中的 912. 排序数组进行测试，这里所求的是升序序列，也即是大根堆实现对无序数组的排序，实现的代码如下：

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
    	//由完全二叉树性质，从非叶子节点/内部节点进行逆序遍历，
    	//右边界下标为nums.size() >> 1;
    	//构建初始的大根堆数据结构
        for(int i = nums.size() >> 1; i >= 0; --i) 
            heapAdjust(nums, i, nums.size());
        //进行首尾元素交换，并重新调整数组元素位置确保剩余元素是大根堆结构
        for(int i = nums.size() - 1; i > 0; --i) {
        	//首位元素交换
            int tmp = nums[i];
            nums[i] = nums[0];
            nums[0] = tmp;
            //调整剩余元素为大根堆
            heapAdjust(nums, 0, i); 
        }
        return nums;
    }

private:
    void heapAdjust(vector<int>& nums, int parent, int size) {
        int tmp = nums[parent]; //记录父节点数值
        int child = parent * 2 + 1; //左节点的下标
        while(child < size) { //当未到达叶子节点
        	//更新child下标，使其等于parent的左右子节点的较大的节点下标
            child = child + 1 < size && nums[child] < nums[child+1] ? child + 1 : child;
            //如果父节点数值大于子节点较大值下标，满足大根堆，跳出
            if(tmp >= nums[child]) break;
            //如果小于，则不满足，进行替换，并继续按照最大子节点的路径进行下沉操作，
            //直至找到父节点数值的合适位置，最终合适位置是parent下标；
            nums[parent] = nums[child]; 
            parent = child; //更新parent
            child = child * 2 + 1; //更新左节点下标
        }
        //可理解为环形数组的移位过程，可以注意到上图构建初始化大根堆中的第(4)图，
        //{3, 8, 7}路径替换为了{8, 7, 3}
        nums[parent] = tmp;
    }
};

4. 复杂度分析

总体情况如下：

时间复杂度：

堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。

其中构建初始堆经推导复杂度为 $O (n)$ ，在交换并重建堆的过程中，需交换 $n - 1$ 次，而重建堆的过程中，根据完全二叉树的性质， $log_2(n-1),log_2(n-2)...1]$ 逐步递减，近似为 $n l o g n$ 。所以堆排序时间复杂度一般认为就是 $O (n l o g n)$ 级。