LeetCode 第 59 场力扣夜喵双周赛（最短路径数+迪杰斯特拉动态规划+最长公共前缀问题） / 第255场周赛（二进制转换，分组背包，子集还原数组（脑筋急转弯））
Posted Zephyr丶J
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了LeetCode 第 59 场力扣夜喵双周赛（最短路径数+迪杰斯特拉动态规划+最长公共前缀问题） / 第255场周赛（二进制转换，分组背包，子集还原数组（脑筋急转弯））相关的知识，希望对你有一定的参考价值。
第 59 场力扣夜喵双周赛
两道400多五百，后两道都写出代码来了，但是都有问题，哭辽…
还有刚开始第一道测试好慢，搞心态了
5834. 使用特殊打字机键入单词的最少时间
有一个特殊打字机，它由一个 圆盘 和一个 指针 组成， 圆盘上标有小写英文字母 ‘a’ 到 ‘z’。只有 当指针指向某个字母时，它才能被键入。指针 初始时 指向字符 ‘a’ 。
每一秒钟，你可以执行以下操作之一：
将指针 顺时针 或者 逆时针 移动一个字符。
键入指针 当前 指向的字符。
给你一个字符串 word ，请你返回键入 word 所表示单词的 最少 秒数 。
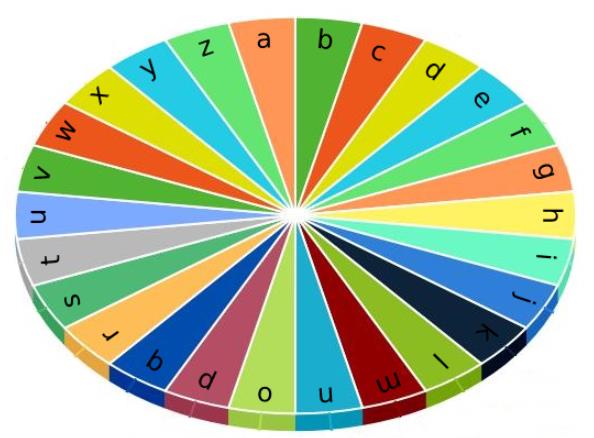
示例 1：
输入：word = “abc”
输出：5
解释：
单词按如下操作键入：
-花 1 秒键入字符 ‘a’ in 1 ，因为指针初始指向 ‘a’ ，故不需移动指针。
-花 1 秒将指针顺时针移到 ‘b’ 。
-花 1 秒键入字符 ‘b’ 。
-花 1 秒将指针顺时针移到 ‘c’ 。
-花 1 秒键入字符 ‘c’ 。
示例 2：
输入：word = “bza”
输出：7
解释：
单词按如下操作键入：
-花 1 秒将指针顺时针移到 ‘b’ 。
-花 1 秒键入字符 ‘b’ 。
-花 2 秒将指针逆时针移到 ‘z’ 。
-花 1 秒键入字符 ‘z’ 。
-花 1 秒将指针顺时针移到 ‘a’ 。
-花 1 秒键入字符 ‘a’ 。
示例 3：
输入：word = “zjpc”
输出：34
解释：
单词按如下操作键入：
-花 1 秒将指针逆时针移到 ‘z’ 。
-花 1 秒键入字符 ‘z’ 。
-花 10 秒将指针顺时针移到 ‘j’ 。
-花 1 秒键入字符 ‘j’ 。
-花 6 秒将指针顺时针移到 ‘p’ 。
-花 1 秒键入字符 ‘p’ 。
-花 13 秒将指针逆时针移到 ‘c’ 。
-花 1 秒键入字符 ‘c’ 。
提示：
1 <= word.length <= 100
word 只包含小写英文字母。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-time-to-type-word-using-special-typewriter
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
题目描述
就是转动呗，比较顺时针还是逆时针转步数少，想像时钟，12个数，0到6，半数是分界线
class Solution {
public int minTimeToType(String word) {
int l = word.length();
int count = l;
char c = 'a';
for(int i = 0; i < l; i++){
char temp = word.charAt(i);
if(Math.abs(temp - c) < 14)
count += Math.abs(temp - c);
else{
count += 26 - Math.abs(temp - c);
}
c = temp;
}
return count;
}
}
5835. 最大方阵和
题目描述
给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：
选择 matrix 中 相邻 两个元素，并将它们都 乘以 -1 。
如果两个元素有 公共边 ，那么它们就是 相邻 的。
你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的 最大 和。
示例 1：
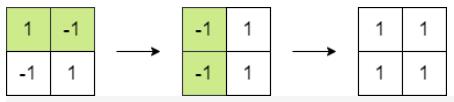
输入：matrix = [[1,-1],[-1,1]]
输出：4
解释：我们可以执行以下操作使和等于 4 ：
-将第一行的 2 个元素乘以 -1 。
-将第一列的 2 个元素乘以 -1 。
示例 2：
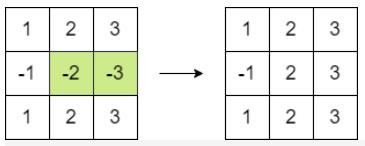
输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
输出：16
解释：我们可以执行以下操作使和等于 16 ：
-将第二行的最后 2 个元素乘以 -1 。
提示：
n == matrix.length == matrix[i].length
2 <= n <= 250
-10^5 <= matrix[i][j] <= 10^5
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-matrix-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
因为第二题，肯定不会让一个个交换的
所以，还是贪心
可以发下，两个相邻数字都乘以-1，如果两个数字都是负数，那么就会变成都是正数，我们期望都是这样的；如果一个正，一个负，那么就可以将负数移动位置；
通过这个规律，如果有偶数个负数，那么通过交换，都可以将负数两两配对，然后最大和就是所有数的绝对值
如果有奇数个负数，那么通过交换，可以使负数只剩下一个，并且可以使这个负数是绝对值最小的数，所以最大和就是整个矩阵的绝对值和，减去这个负数绝对值×2
class Solution {
public long maxMatrixSum(int[][] matrix) {
//想想
int min = Integer.MAX_VALUE;
int n = matrix.length;
long sum = 0;
int count = 0;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
count += matrix[i][j] > 0 ? 0 : 1;
min = Math.min(matrix[i][j] > 0 ? matrix[i][j] : -matrix[i][j], min);
sum += matrix[i][j] > 0 ? matrix[i][j] : -matrix[i][j];
}
}
return count % 2 == 0? sum : sum - min - min;
}
}
5836. 到达目的地的方案数
题目描述
你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。
给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。
请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 109 + 7 取余 后返回。
示例 1：
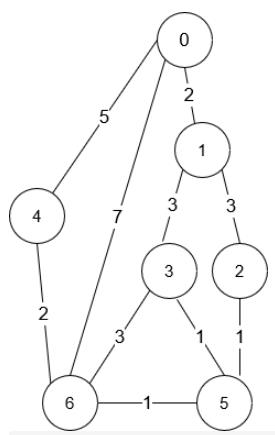
输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
示例 2：
输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。
提示：
1 <= n <= 200
n - 1 <= roads.length <= n * (n - 1) / 2
roads[i].length == 3
0 <= ui, vi <= n - 1
1 <= timei <= 109
ui != vi
任意两个路口之间至多有一条路。
从任意路口出发，你能够到达其他任意路口。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-ways-to-arrive-at-destination
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
dfs肯定会超时，但是我想的是先写个dfs，然后记忆化优化一下，结果想了半天也不知道怎么优化
然后也想到了最短路，但是感觉最短路都是求到所有点的路，感觉用不上，就跳了
当时的dfs代码，十几个例子就超时了：
class Solution {
long min = 0;
int count = 0;
Map<Integer, Map<Integer, Integer>> map;
int n;
boolean[] used;
int MOD = (int)1e9 + 7;
long[][] memo;
public int countPaths(int n, int[][] roads) {
//先写个暴力看看行不行吧
this.n = n;
int l = roads.length;
used = new boolean[n];
map = new HashMap<>();
memo = new long[n][n]; //两点之间花费的时间
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
memo[i][j] = Long.MAX_VALUE;
}
}
for(int i = 0; i < l; i++){
int[] temp = roads[i];
Map<Integer, Integer> in = map.getOrDefault(temp[0], new HashMap<>());
in.put(temp[1], temp[2]);
map.put(temp[0], in);
Map<Integer, Integer> in2 = map.getOrDefault(temp[1], new HashMap<>());
in2.put(temp[0], temp[2]);
map.put(temp[1], in2);
}
dfs(0, 0);
return count;
}
public void dfs(int k, long time){
if(k == n - 1){
if(min == 0 || time < min){
min = time;
count = 1;
}
else if(time == min){
count += 1;
}
return;
}
Map<Integer, Integer> temp = map.get(k);
for(int r : temp.keySet()){
if(used[r])
continue;
if(min != 0 && time + temp.get(r) > min)
continue;
used[r] = true;
dfs(r, time + temp.get(r));
used[r] = false;
}
}
}
不会做，想不到咋做？
看了官解，然后又看了讨论里写的答案，仔细思考了一下
说到底，是先求最短路，再统计最短路的数量
而迪杰斯特拉本来就是求到每个节点最短路的算法，而在到达最短路的同时，也可以用一个数组记录到达每个节点最短路的数量大小
先写了个这个代码，然后第45个例子报错了，原因是因为超整数范围了
class Solution {
public static final int MOD = (int)1e9 + 7;
public int countPaths(int n, int[][] roads) {
//先用迪杰斯特拉处理，计算出到每个点的最短路
//然后再用最短路创建一个有向无环图，然后再图上dfs找到达n-1最短路的数目
//但是迪杰斯特拉求最短路的时候，就可以用一个数组记录达到每个点最短路的数目
//首先还是要预处理每两个点之间的距离
int l = roads.length;
if(n == 1)
return 1;
Map<Integer, Map<Integer, Integer>> map = new HashMap<>();
for(int i = 0; i < l; i++){
int[] temp = roads[i];
Map<Integer, Integer> in = map.getOrDefault(temp[0], new HashMap<>());
in.put(temp[1], temp[2]);
map.put(temp[0], in);
Map<Integer, Integer> in2 = map.getOrDefault(temp[1], new HashMap<>());
in2.put(temp[0], temp[2]);
map.put(temp[1], in2);
}
int[] dist = new int[n]; //到达每个点的最小路径距离
Arrays.fill(dist, Integer.MAX_VALUE);
int[] count = new int[n]; //每个点最短路的数目
//从0到0路径一条
count[0] = 1;
//迪杰斯特拉算法
//存放点和距离
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b) -> (a[1] == b[1] ? a[0] - b[0] : a[1] - b[1]));
//初始，从0点到达0的距离是0
pq.offer(new int[]{0, 0});
while(!pq.isEmpty()){
int[] top = pq.poll();
int p = top[0];
int d = top[1];
//System.out.print(p + " ");
//System.out.println(d);
//如果超过了最短路径，那么就跳过
if(d > dist[p])
continue;
//取出与p相连的节点，把它们都加到优先队列中，距离要累计
Map<Integer, Integer> rlt = map.get(p);
for(int key : rlt.keySet()){
//如果距离大于最短距离，跳过；
if(rlt.get(key) + d > dist[key])
continue;
//如果等于最短路，那么通过这条路到达最短路的路径数就是count[p]
if(rlt.get(key) + d == dist[key]){
count[key] = (count[key] + count[p]) % MOD;
}else{
//如果小于最短路，那么就加入优先队列
pq.offer(new int[]{key, rlt.get(key) + d});
//更新最短路，同时更新count数组
dist[key] = rlt.get(key) + d;
count[key] = (count[key] + count[p]) % MOD;;
}
}
}
return count[n - 1];
}
}
然后我就想都改成long就完事了呗，然后：
PriorityQueue<long[]> pq = new PriorityQueue<>((a,b) -> (a[1] == b[1] ? a[0] - b[0] : a[1] - b[1]));
这样写，一直出错，放到idea里一看，原因是因为，compare函数，也就是默认用的比较函数的返回值是int，这样写的话，相减结果是long，所以要转换成int
也就是这样：
PriorityQueue<long[]> pq = new PriorityQueue<>((a,b) -> (int)(a[1] == b[1] ? a[0] - b[0] : a[1] - b[1]));
以为这样就可以了，结果一提交，变成过了44个，醉了，我是不知道咋改了
然后看到个这样的代码，全部用的int，还能过，咱也不知道为啥了，就这样吧，思路懂了就行了
class Solution {
public int countPaths(int n,int[][] times) {
final int INF = Integer.MAX_VALUE;
List<int[]>[] g = new List[n];
for (int i = 0; i < n; ++i) {
g[i] = new ArrayList<int[]>();
}
for (int[] t : times) {
int x = t[0] , y = t[1];
g[x].add(new int[]{y, t[2]});
g[y].add(new int[]{x, t[2]});
}
int mod=1000000007;
int[][] dist = new int[n][2];
for (int i = 0; i < n; i++) {
dist[i][0] = INF;
}
dist[0][0] = 0;
dist[0][1] = 1;
int ans = 0;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>((a, b) -> a[0] != b[0] ?以上是关于LeetCode 第 59 场力扣夜喵双周赛（最短路径数+迪杰斯特拉动态规划+最长公共前缀问题） / 第255场周赛（二进制转换，分组背包，子集还原数组（脑筋急转弯））的主要内容，如果未能解决你的问题，请参考以下文章
LeetCode第 57 场力扣夜喵双周赛（差分数组单调栈） and 第 251 场力扣周赛（状态压缩动规，树的序列化，树哈希，字典树）
LeetCode494. 目标和 / 474. 一和零 / 203. 移除链表元素 / 第 244 场力扣周赛
第 256 场力扣周赛（状态压缩+dp，二进制子序列的动规940）