❤️《画解数据结构》全网最清晰哈希表入门，三张动图搞懂哈希 ❤️(建议收藏)
Posted 英雄哪里出来
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了❤️《画解数据结构》全网最清晰哈希表入门，三张动图搞懂哈希 ❤️(建议收藏)相关的知识，希望对你有一定的参考价值。
零、前言
「 数据结构 」 和 「 算法 」 是密不可分的，两者往往是「 相辅相成 」的存在，所以，在学习 「 数据结构 」 的过程中，不免会遇到各种「 算法 」。
数据结构 常用的操作一般为：「 增 」「 删 」「 改 」「 查 」。基本上所有的数据结构都是围绕这几个操作进行展开的。
那么这篇文章，作者将用 「 三张动图 」 来阐述一种 「 均摊 O（1） 」 的数据结构
「 哈希表 」
🙉饭不食，水不饮，题必须刷🙉
C语言免费动漫教程，和我一起打卡！ 🌞《光天化日学C语言》🌞
LeetCode 太难？先看简单题！ 🧡《C语言入门100例》🧡
数据结构难？不存在的！ 🌳《画解数据结构》🌳
LeetCode 太简单？算法学起来！ 🌌《夜深人静写算法》🌌
哈希表常用的方法是 开放定址法 和 链地址法：
开放定址法
链地址法
看不懂没有关系，我会把它拆开来一个一个讲，首先来看一下今天要学习的内容目录。
一、哈希表的概念
1、查找算法
当我们在一个 链表 或者 顺序表 中 查找 一个数据元素 是否存在 的时候，唯一的方法就是遍历整个表，这种方法称为 线性枚举。
如果这时候，顺序表是有序的情况下，我们可以采用折半的方式去查找，这种方法称为 二分枚举。
线性枚举 的时间复杂度为
O
(
n
)
O(n)
O(n)。二分枚举 的时间复杂度为
O
(
l
o
g
2
n
)
O(log_2n)
O(log2n)。是否存在更快速的查找方式呢？这就是本要介绍的一种新的数据结构 —— 哈希表。
2、哈希表
由于它不是顺序结构，所以很多数据结构书上称之为 散列表，下文会统一采用 哈希表 的形式来说明，作为读者，只需要知道这两者是同一种数据结构即可。
我们把需要查找的数据，通过一个 函数映射，找到 存储数据的位置 的过程称为 哈希。这里涉及到几个概念：
a）需要 查找的数据 本身被称为 关键字；
b）通过 函数映射 将 关键字 变成一个 哈希值 的过程中，这里的 函数 被称为 哈希函数；
c）生成 哈希值 的过程过程可能产生冲突，需要进行 冲突解决；
d）解决完冲突以后，实际 存储数据的位置 被称为 哈希地址，通俗的说，它就是一个数组下标；
e）存储所有这些数据的数据结构就是 哈希表，程序实现上一般采用数组实现，所以又叫 哈希数组。整个过程如下图所示：
2、哈希数组
为了方便下标索引，哈希表 的底层实现结构是一个数组，数组类型可以是任意类型，每个位置被称为一个槽。如下图所示，它代表的是一个长度为 8 的 哈希表，又叫 哈希数组。
3、关键字
关键字 是哈希数组中的元素，可以是任意类型的，它可以是整型、浮点型、字符型、字符串，甚至是结构体或者类。如下的 A、C、M 都可以是关键字；
int A = 5;
char C[100] = "Hello World!";
struct Obj { };
Obj M;
哈希表的实现过程中，我们需要通过一些手段，将一个非整型的 关键字 转换成 数组下标，也就是 哈希值，从而通过
O
(
1
)
O(1)
O(1) 的时间快速索引到它所对应的位置。
而将一个非整型的 关键字 转换成 整型 的手段就是 哈希函数。
4、哈希函数
哈希函数可以简单的理解为就是小学课本上那个函数，即
y
=
f
(
x
)
y = f(x)
y=f(x)，这里的
f
(
x
)
f(x)
f(x) 就是哈希函数，
x
x
x 是关键字，
y
y
y 是哈希值。好的哈希函数应该具备以下两个特质：
a）单射；
b）雪崩效应：输入值
x
x
x 的
1
1
1 比特的变化，能够造成输出值
y
y
y 至少一半比特的变化；
单射很容易理解，图
(
a
)
(a)
(a) 中已知哈希值
y
y
y 时，键
x
x
x 可能有两种情况，不是一个单射；而图
(
b
)
(b)
(b) 中已知哈希值
y
y
y 时，键
x
x
x 一定是唯一确定的，所以它是单射。由于
x
x
x 和
y
y
y 一一对应，这样就从本原上减少了冲突。
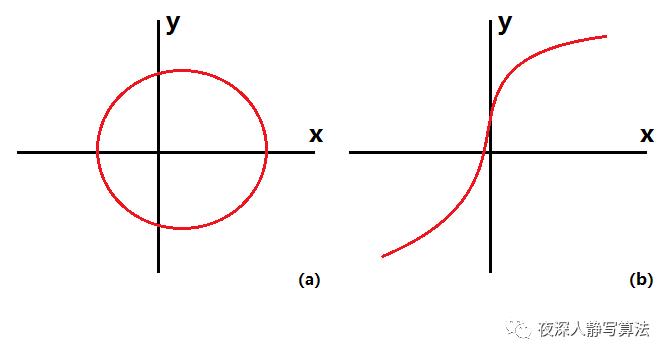雪崩效应是为了让哈希值更加符合随机分布的原则，哈希表中的键分布的越随机，利用率越高，效率也越高。
常用的哈希函数有：直接定址法、除留余数法、数字分析法、平方取中法、折叠法、随机数法 等等。有关哈希函数的内容，下文会进行详细讲解。
5、哈希冲突
哈希函数在生成 哈希值 的过程中，如果产生 不同的关键字得到相同的哈希值 的情况，就被称为 哈希冲突。
即对于哈希函数
y
=
f
(
x
)
y = f(x)
y=f(x)，当关键字
x
1
≠
x
2
x_1 \\neq x_2
x1=x2，但是却有
f
(
x
1
)
=
f
(
x
2
)
f(x_1) = f(x_2)
f(x1)=f(x2)，这时候，我们需要进行冲突解决。
冲突解决方法有很多，主要有：开放定址法、再散列函数法、链地址法、公共溢出区法 等等。有关解决冲突的内容，下文会进行详细讲解。
6、哈希地址
哈希地址 就是一个 数组下标 ，即哈希数组的下标。通过下标获得数据，被称为 索引。通过数据获得下标，被称为 哈希。平时工作的时候，和同事交流时用到的一个词 反查 就是说的 哈希。
二、常用哈希函数
1、直接定址法
直接定址法 就是 关键字 本身就是 哈希值，表示成函数值就是 f ( x ) = x f(x) = x f(x)=x 例如，我们需要统计一个字符串中每个字符的出现次数，就可以通过这种方法。任何一个字符的范围都是 [ 0 , 255 ] [0, 255] [0,255]，所以只要用一个长度为 256 的哈希数组就可以存储每个字符对应的出现次数，利用一次遍历枚举就可以解决这个问题。C代码实现如下：
int i, hash[256];
for(i = 0; str[i]; ++i) {
++hash[ str[i] ];
}
这个就是最基础的直接定址法的实现。hash[c]代表字符c在这个字符串str中的出现次数。
2、平方取中法
平方取中法 就是对 关键字 进行平方，再取中间的某几位作为 哈希值。
例如，对于关键字
1314
1314
1314，得到平方为
1726596
1726596
1726596，取中间三位作为哈希值，即
265
265
265。
平方取中法 比较适用于 不清楚关键字的分布，且位数也不是很大 的情况。
3、折叠法
折叠法 是将关键字分割成位数相等的几部分（注意最后一部分位数不够可以短一些），然后再进行求和，得到一个 哈希值。
例如，对于关键字
5201314
5201314
5201314，将它分为四组，并且相加得到：
52
+
01
+
31
+
4
=
88
52+01+31+4 = 88
52+01+31+4=88，这就是哈希值。
折叠法 比较适用于 不清楚关键字的分布，但是关键字位数较多 的情况。
4、除留余数法
除留余数法 就是 关键字 模上 哈希表 长度，表示成函数值就是
f
(
x
)
=
x
m
o
d
m
f(x) = x \\ mod \\ m
f(x)=x mod m 其中
m
m
m 代表了哈希表的长度，这种方法，不仅可以对关键字直接取模，也可以在 平方取中法、折叠法 之后再取模。
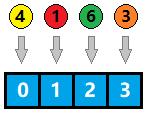
例如，对于一个长度为 4 的哈希数组，我们可以将关键字 模 4 得到哈希值，如图所示：
5、位与法
哈希数组的长度一般选择 2 的幂，因为我们知道取模运算是比较耗时的，而位运算相对较为高效。
选择 2 的幂作为数组长度，可以将 取模运算 转换成 二进制位与。
令
m
=
2
k
m = 2^k
m=2k，那么它的二进制表示就是：
m
=
(
1
000...000
⏟
k
)
2
m = (1\\underbrace{000...000}_{\\rm k})_2
m=(1k
000...000)2，任何一个数模上
m
m
m，就相当于取了
m
m
m 的二进制低
k
k
k 位，而
m
−
1
=
(
111...111
⏟
k
)
2
m-1 = (\\underbrace{111...111}_{\\rm k})_2
m−1=(k
111...111)2 ，所以和 位与
m
−
1
m-1
m−1 的效果是一样的。即：
x
%
S
=
=
x
&
(
S
−
1
)
x \\ \\% \\ S == x \\ \\& \\ (S - 1)
x % S==x & (S−1) 除了直接定址法，其它三种方法都有可能导致哈希冲突，接下来，我们就来讨论下常用的一些哈希冲突的解决方案。
三、常见哈希冲突解决方案
1、开放定址法
1）原理讲解
开放定址法 就是一旦发生冲突，就去寻找下一个空的地址，只要哈希表足够大，总能找到一个空的位置，并且记录下来作为它的 哈希地址。公式如下：
f
i
(
x
)
=
(
f
(
x
)
+
d
i
)
m
o
d
m
f_i(x) = (f(x)+d_i) \\ mod \\ m
fi(x)=(f(x)+di) mod m
这里的
d
i
d_i
di 是一个数列，可以是常数列
(
1
,
1
,
1
,
.
.
.
,
1
)
(1, 1, 1, ...,1)
(1,1,1,...,1)，也可以是等差数列
(
1
,
2
,
3
,
.
.
.
,
m
−
1
)
(1,2,3,...,m-1)
(1,2,3,...,m−1)。
2）动画演示
上图中，采用的是哈希函数算法是 除留余数法，采用的哈希冲突解决方案是 开放定址法，哈希表的每个数据就是一个关键字，插入之前需要先进行查找，如果找到的位置未被插入，则执行插入；否则，找到下一个未被插入的位置进行插入；总共插入了 6 个数据，分别为：11、12、13、20、19、28。
这种方法需要注意的是，当插入数据超过哈希表长度时，不能再执行插入。
本文在第四章讲解 哈希表的现实 时采用的就是常数列的开放定址法。
2、再散列函数法
1）原理讲解
再散列函数法 就是一旦发生冲突，就采用另一个哈希函数，可以是 平方取中法、折叠法、除留余数法 等等的组合，一般用两个哈希函数，产生冲突的概率已经微乎其微了。
再散列函数法 能够使关键字不产生聚集，当然，也会增加不少哈希函数的计算时间。
2）动画演示
待补充
3、链地址法
1）原理讲解
当然，产生冲突后，我们也可以选择不换位置，还是在原来的位置，只是把 哈希值 相同的用链表串联起来。这种方法被称为 链地址法。
2）动画演示
上图中，采用的是哈希函数算法是 除留余数法，采用的哈希冲突解决方案是 链地址法，哈希表的每个数据保留了一个 链表头结点 和 尾结点，插入之前需要先进行查找，如果找到的位置，链表非空，则插入尾结点并且更新尾结点；否则，生成一个新的链表头结点和尾结点；总共插入了 6 个数据，分别为：11、12、13、20、19、28。
4、公共溢出区法
1）原理讲解
一旦产生冲突的数据，统一放到另外一个顺序表中，每次查找数据，在哈希数组中到的关键字和给定关键字相等，则认为查找成功；否则，就去公共溢出区顺序查找，这种方法被称为 公共溢出区法。
这种方法适合冲突较少的情况。
2）动画演示
待补充
四、哈希表的实现
1、数据结构定义
由于哈希表的底层存储还是数组，所以我们可以定义一个结构体，结构体中定义一个数组类型的成员，如果需要记录哈希表元素的个数，还可以记录一个 size字段。
C语言实现如下：
#define maxn (1<<17) /以上是关于❤️《画解数据结构》全网最清晰哈希表入门，三张动图搞懂哈希 ❤️(建议收藏)的主要内容，如果未能解决你的问题，请参考以下文章
❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)
❤️《画解数据结构》两万字，十张动图，画解双端队列❤️(建议收藏)
❤️《画解数据结构》全网最全队列总结，九张动图搞懂队列 ❤️(文末有投票)