AtCoder Beginner Contest 171(补题)

Posted 2021-09-08 佐鼬Jun

C - One Quadrillion and One Dalmatians

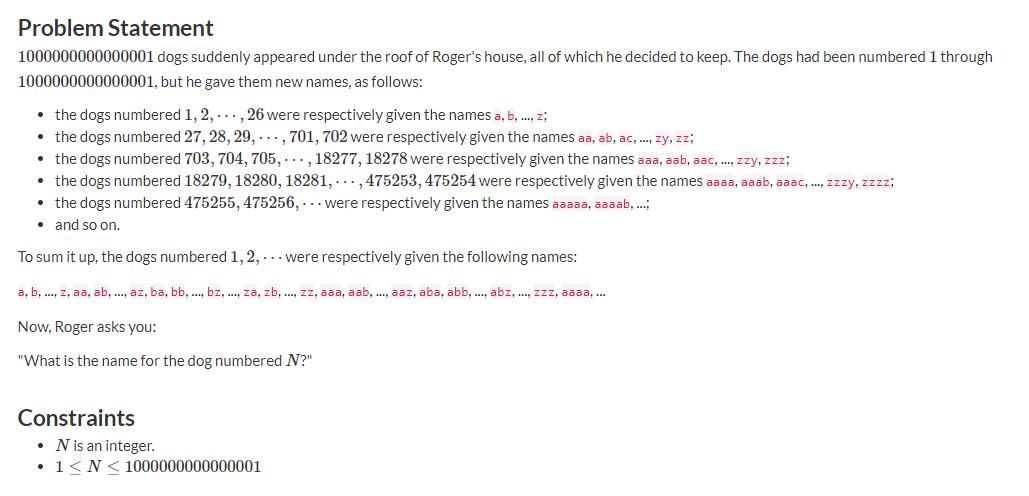
题意：

现在$1到26$的数字为$a到z$，$27$到$702$数字为 aa, ab, ac, …, zy, zz,475255,475256为aaaaa, aaaab，现在给你数字$n$,让你输出对应的字符串

思路：

26个字母，所以转换为26进制，每次取余前，要减去1，把$[1,26]$映射到$[0,25]$，然后输出即可

#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll n;
stack<int> sta;

int main() {
    cin >> n;
    while (n) {
        n--;
        sta.push(n % 26);
        n /= 26;
    }
    while (!sta.empty()) {
        int x = sta.top();
        sta.pop();
        printf("%c", x + 'a');
    }
    return 0;
}

F - Strivore

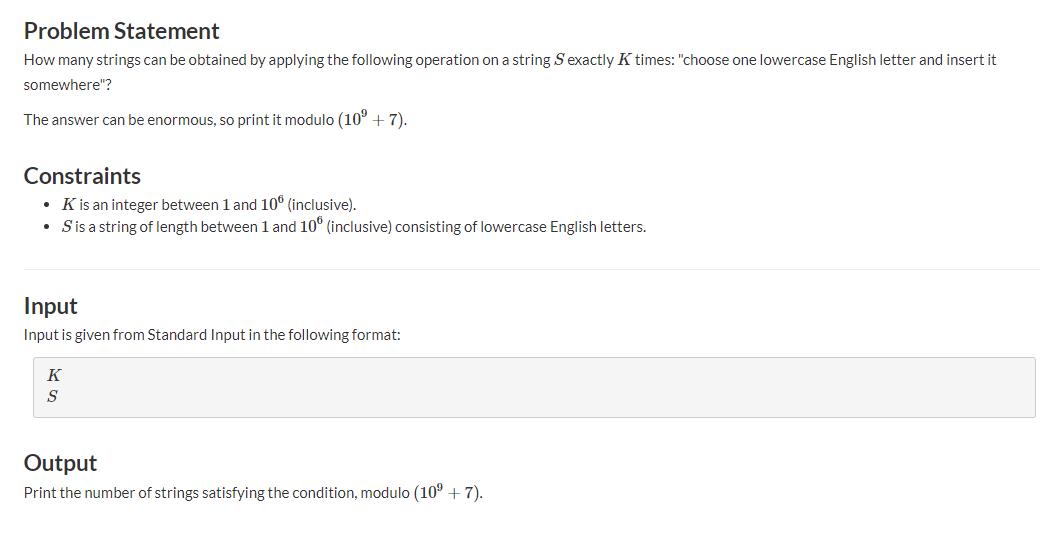
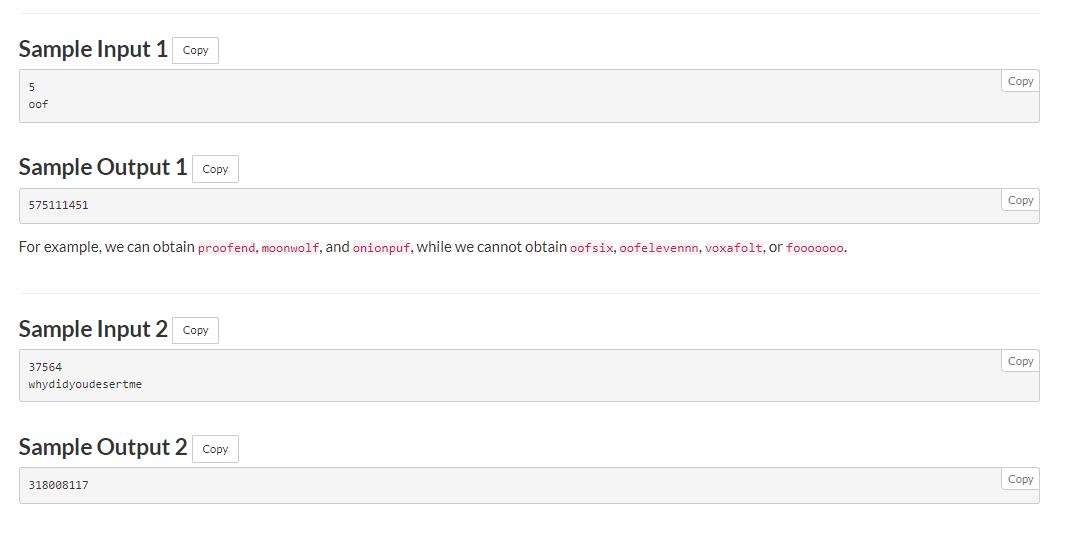
题意：

给一个长度为$m$字符串，现在可以往字符串里加任意字符，可以加$n$次，问最终会形成多少种字符串，答案对$10^9+7$取模

思路：

组合数(排列组合)+去重+快速幂+逆元
加$n$次字符，最终字符串长度是$n+m$，现在先确定$s$字符串的第一个字母的位置在$i$号位置$(1<=i<=n+1)$，那么此时$i$号位置前面的每个位置的字母情况都是26，所以就是$26^{i-1}$,$i$后面的位置，先从后面的位置选出$s$串剩下$m-1$个字母的位置，由于相对顺序是固定的，所以是$C_{n+m-i}^{m-1}$然后每个 $s$ 串字母后面不选相同的字母，用于去重，所以是$25^{n+m-i-m+1}$，即$25^{n-i+1}$种情况，
小证明： 若有个$s$字符串为$abc$
那么枚举位置$i$的时候，会有这种情况， _____a()()()()b______c
如果a的第二个位置填了a，就是_____aa()()()b______c
那么下次枚举第一个字母a位置的位置，为下一个位置$i+1$
也就是_____a()()()b______c
而此时这个a前面由于是26种情况
肯定会有_____aa()()()b______c
所以重复，这里枚举的是第二个位置，后面的位置同理如此
下面代码由于$i$是从0开始循环到$n$,所以公式有-1的差距
公式：$\sum _{i=0}^n$$\cdot 26^i$$\cdot C_{n+m-i-1}^{m-1}$$\cdot 25^{n-i}$

#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
const int N = 1e6 + 10;
#define ll long long
string s;
int n;
ll fact[N*2], infact[N*2];
ll qmi(ll a, ll k, ll p) {
    ll res = 1;
    while (k) {
        if (k & 1) res = (ll)res * a % p;
        a = (ll)a * a % mod;
        k >>= 1;
    }
    return res;
}
void init() {
    fact[0] = infact[0] = 1;
    for (int i = 1; i < 2*N; i++) {
        fact[i] = (ll)fact[i - 1] * i % mod;
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}
ll C(int a, int b) { return fact[a] * infact[b] % mod * infact[a - b] % mod; }
int main() {
    init();
    cin >> n >> s;
    ll res = 0;
    int m = s.size();
    for (int i = 0; i <= n; i++) {
        res = (ll)res + qmi(26, i, mod) % mod * C(n + m - i - 1, m - 1) % mod *
                            qmi(25, n - i, mod) % mod;
    }
    cout << res % mod << endl;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激