Leetcode---通配符匹配

Posted 2021-09-08 可乐不解渴

🌏时光匆匆流逝过，平平淡淡才是真。
忍耐任由风雨过，守得云开见月明。

🚩题目描述

给定一个字符串 (s) 和一个字符模式 § ，实现一个支持 ‘?’ 和 ‘’ 的通配符匹配。
’ ? ’ 可以匹配任何单个字符。
’ * ’ 可以匹配任意字符串（包括空字符串）。
两个字符串完全匹配才算匹配成功。
说明:
s可能为空，且只包含从 a-z 的小写字母。
p可能为空，且只包含从 a-z 的小写字母，以及字符 ? 和 * 。
示例 1:
输入:s = “adceb” 和 p = “ab”
输出: true
解释: 第一个 '’ 可以匹配空字符串, 第二个 ‘*’ 可以匹配字符串 "dce"
题目链接：https://leetcode-cn.com/problems/wildcard-matching。

🛫解题思路

🎢动态规划

我们知道要想达到字符串是否匹配，我们是从头一个一个的字符来一一比对，最后来知道是否两个字符串匹配的。
在给定的模式 p 中，只会有三种类型的字符出现：

• 小写字母 a-za−z，可以匹配对应的一个小写字母；

• 问号 ‘ ? ’ ，可以匹配任意一个小写字母；

• 星号 ’∗‘，可以匹配任意字符串，可以为空，也就是匹配零或任意多个小写字母。
  其中小写字母和问号的匹配是确定的，而星号的匹配是不确定的，星号可以匹配任意多个，因此我们需要枚举所有的匹配情况，一旦进行枚举就会造成重复子问题的出现，所以我们这里进行动态规划来减少子问题的重复计算。
  首先那么我们定义：dp[i][j] 表示 s前 i个字符和p的前j个字符是否匹配。
  在我们确定的情况当中：
  1、当p[j]是小写字母时，那么s[i]也一定是小写字母才能进行匹配成功。所以状态转移方程为：

    dp[i][j]=dp[i-1][j-1]            si与pi相等时，此时p[j]是小写字母
  

2、当p[j]是**‘？’时，除了空字符外，可以匹配任何一个字符。所以我们得出‘？’**状态转移方程为：

     dp[i][j]=dp[i-1][j-1]            当p[j]==‘?’时

3、最后就是我们的 ’∗‘，那么同样对s[i]没有任何要求，但是星号可以匹配零或任意多个小写字母，因此状态转移方程分为两种情况，即使用或不使用这个星号来进行匹配：

	dp[i][j]=dp[i][j−1]||dp[i−1][j]		当p[j]==‘*’时

可能有人会迷惑为什么会这么定义，怎么来的呢？

🎡举例

举个例子首先我们假设匹配模式为p = “a*c?b”，s = “acdcb”
1、

• 此时匹配模式p第一个字符p[0]是小写字母，那么s[0]就必须得是小写字母。那么为什么会dp[i][j]=dp[i-1][j-1]，这是因为我们这两个字符虽然匹配了，不一定就匹配，这要看其前面的全部字符是否匹配，如果前面的字符都匹配成功了，我们这里才能算匹配成功。

2、

• 我们发现p[1]==’ * ',因为 * 号可以匹配任何的字符（包括空字符），对s是什么字符没有任何的要求。为什么会定义成 dp[i][j]=dp[i][j−1]||dp[i−1][j] 呢？这是因为要看一下前面的匹配模式字符s[1]有没有匹配p[0]这个位置的字符，如果匹配了那么这里的 ’ * ‘ 号也就匹配了。
• 还有还要查看这里的 ‘ * ’ 号是否将前面的部分字符全部匹配，如果是的话，那么这里同样也是匹配的，相反则不匹配。即dp[i−1][j]。

3、

• 最后就算这个❓号了，它与普通字符串一样，除了不是空字符串都能匹配。❓是否匹配了，还得查看该位置的前面的全部字符是否匹配。前一个字符匹配了，则该位置就匹配；相反则不匹配。

✨边界情况

在动态规划前，我们还要进行一些边界情况。
dp[0][0]=true，即当字符串 s 和模式 p 均为空时，匹配成功；
dp[i][0]=false，即空模式无法匹配非空字符串；这步我们可以在创建dp时，将dp的初始值全部初始化为false来解决。
dp[0][j]需要分情况讨论：因为星号才能匹配空字符串，所以只有当模式串p的前j个字符均为星号时，dp[0][j]才为真。 针对这一步我们需要用一个循环来特殊化处理空字符串与每一个字符的匹配情况。
如下图所示：

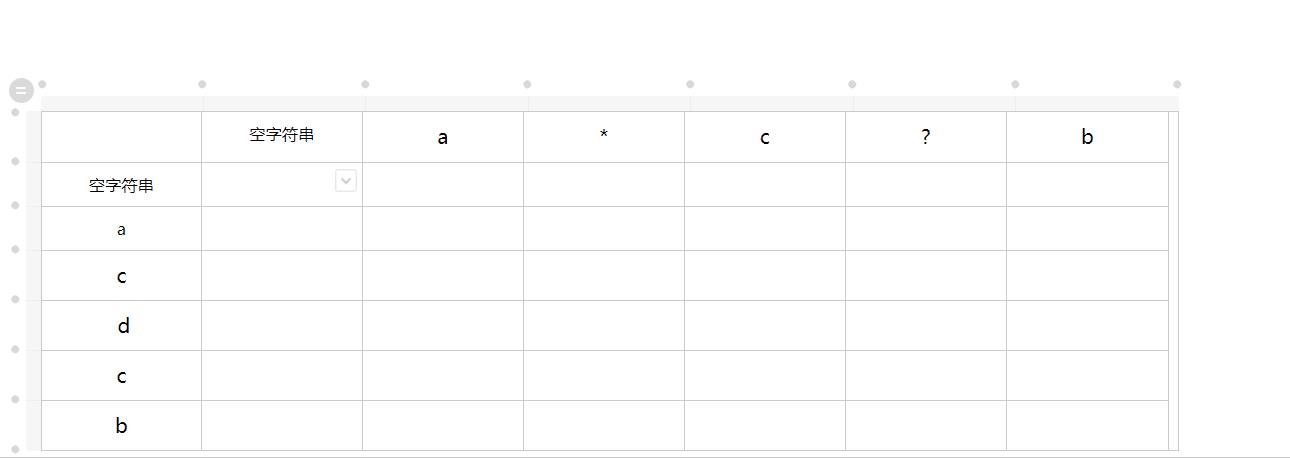
💺填表演示

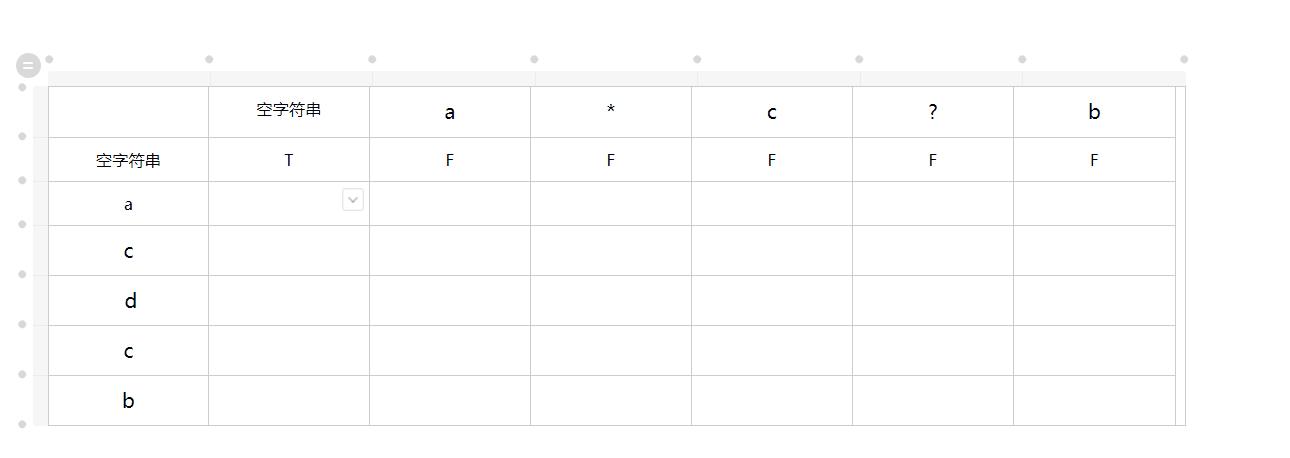
在上面的填表中，我们已经填完了每一种匹配方式的状态，最后右下角的匹配结果就是我们本题的最后答案所在。

🛬解题代码

class Solution 
{
public:
    // 状态转移方程：
    //      1. 当 s[i] == p[j]，或者 p[j] == ? 那么 dp[i][j] = dp[i - 1][j - 1];
    //      2. 当 p[j] == * 那么 dp[i][j] = dp[i][j - 1] || dp[i - 1][j]    
    // 其中:dp[i][j - 1] 表示 * 代表的是空字符，例如 a, *
    //      dp[i - 1][j] 表示 * 代表的是非空字符，例如 abc, ab*
    // 初始化：
    //      1. dp[0][0] 表示什么都没有，其值为 true
    //      2. 第一行 dp[0][j]，换句话说，s 为空，与 p 匹配，所以只要 p 开始为 * 才为 true
    //      3. 第一列 dp[i][0]，当然全部为 false
    bool isMatch(string s, string p) 
    {
        size_t S_size=s.size();
        size_t P_size=p.size();

        // 状态定义：dp[i][j] 表示 s 的前 i 个字符和 p 的前 j 个字符是否匹配
        vector<vector<bool>> dp(S_size + 1, vector<bool>(P_size + 1,false));
        // 1.初始化 空字符串与空字符串是匹配的
        dp[0][0]=true;
        for(size_t i=1;i<=P_size;++i)
        {
            if(p[i - 1]=='*')       //2.空字符串和*是匹配的
            {
                dp[0][i]=dp[0][i-1];
            }
        }
        
        for (size_t i = 1; i <= S_size; ++i) //状态转移
        {
            for (size_t j = 1; j <= P_size; ++j) 
            {
                if (p[j - 1] == '*') 
                {
                    dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
                }
                else if (p[j - 1] == '?' || s[i - 1] == p[j - 1]) 
                {
                    dp[i][j] = dp[i - 1][j - 1];
                }
            }
        }
        return dp[S_size][P_size];
    }
};

🎠效率

时间复杂度：O(mn)。
空间复杂度：O(mn)O(mn)。

如果小伙伴还没看懂可以在评论区留言，我会在评论区给你解答！
如有错误之处还请各位指出！！！
那本篇文章就到这里啦，下次再见啦！